Subscribe to our subreddit to get all the updates from the team!

A friend and I are making a rogue-lite retro procedural game. As in many procedural rogue-lite games, it will have rooms to complete but also the notion of zones. The difference between a zone and a room is that a zone is open air whilst a room is not. Rooms are connected mainly by corridors while zones are mostly naturally connected / separated by rivers and mountains.

Because we want levels with zones to be generated, we need to tame the beast that is procedural generation. How can we generate each zone itself and also clearly divide them? Until now, I had only been using the Java noise library called Joise, which is the Java community port of JTippetts' Accidental Noise Library. I needed the zone data to be generated with basis function modules, i.e. Perlin noise, but in contrast I needed a more structured approach for the zone division. Joise library does have a cell noise module that is a Worley noise. It looks like this depending on its 4 parameters (1, 0, 0, 0) :

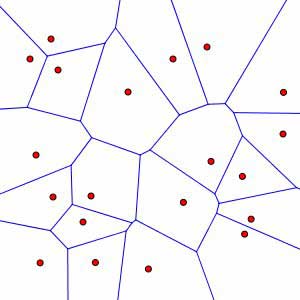
Using math modules, I was able to morph that noise into something that looks like a Voronoi diagram. Here's what a Voronoi diagram should look like (never mind the colors, the important parts are the cell edges and the cell centers) :

A more aesthetic version :

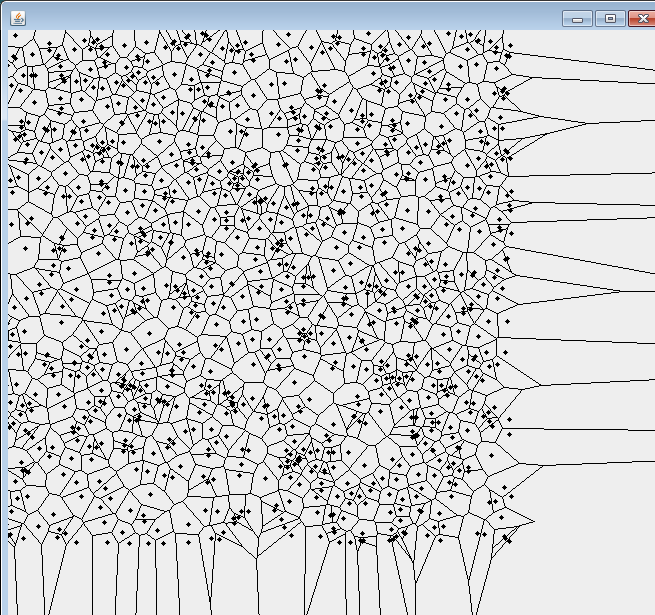
The Worley noise that I had morphed into a Voronoi-like diagram did not include the cell centers, did not include metadata about the edges and was not enough deterministic in a sense that sometimes, the edges would around 60 pixels large. I then searched for a Java Voronoi library and found this one called Voronoi-Java. With this, I was able to generate simple Voronoi diagrams :

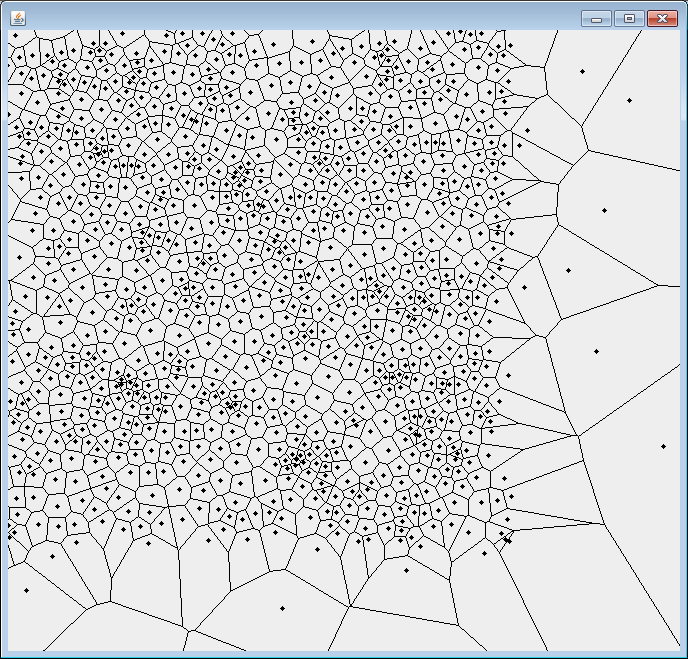
Relaxed : 1 iteration

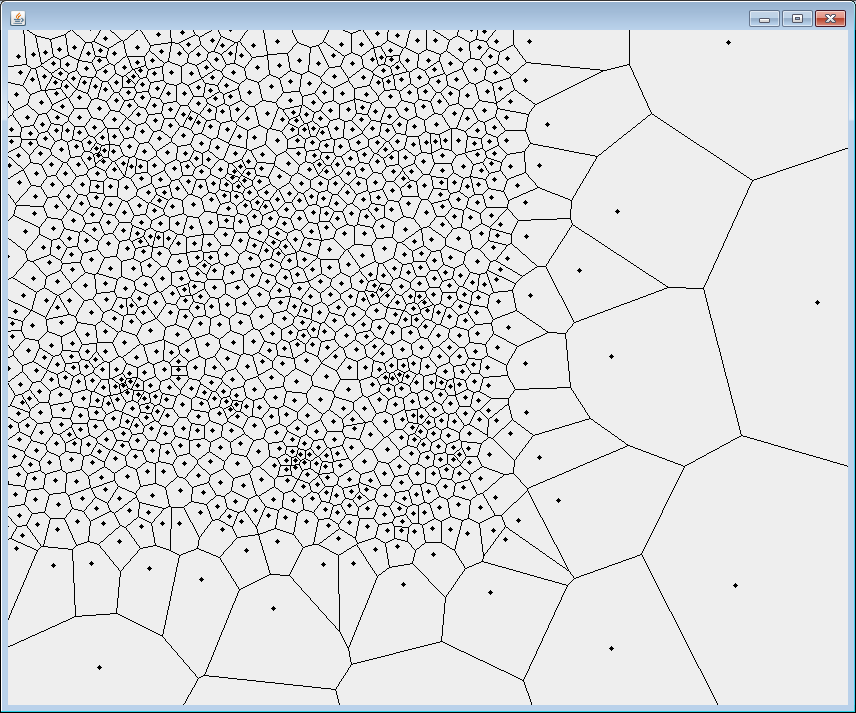
Relaxed : 2 iterations

The relaxation concept is actually the Lloyd's algorithm fortunately included within the library.

Now how can I make that diagram respect my level generation mechanics? Well, if we can limit an approximated number of cells within a certain resolution, that would be a good start. The biggest problem here, is that the relaxation reduces the number of cells within a restricted resolution (contrary to the global resolution) and so we need to keep that in mind.

To do that, I define a constant for the total number of sites / cells. Here's my code :

private Voronoi createVoronoiDiagram(int resolution) { Random random = new Random(); Stream<Point> gen = Stream.generate(() -> new Point(random.nextDouble() * resolution, random.nextDouble() * resolution)); return new Voronoi(gen.limit(VORONOI_SITE_COUNT).collect(Collectors.toList())).relax().relax().relax(); }

A brief pseudo-code of the algorithm would be the following :

1. Create the Voronoi diagram
2. Find the centermost zone
3. Selects X number of zones while there are zones that respect the selection criteria
4. Draw the border map
5. Draw the smoothed border map

The selection criteria is applied for each edge that is connected only to one selected zone. Here's the selection criteria :

• Is connected to a closed zone, i.e. that all its edges form a polygon
• Does have two vertices
• Is inclusively in the resolution's boundaries

Here's the result of a drawn border map!

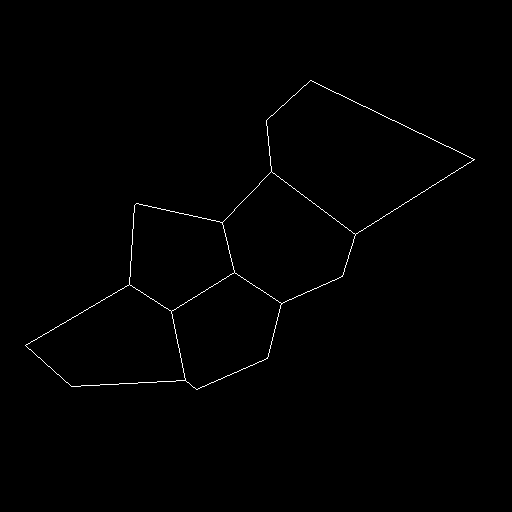
In this graph, I have a restricted number of cells that follow multiple criteria and I know each edge and each cell center point.

To draw the smoothed border map, the following actions must be taken : emit colors from already drawn pixels and then apply a gaussian blur. Personally, I use the JH Labs Java Image Filters library for the gaussian blur.

With color emission only :

With color emission and a gaussian blur :

You may ask yourself why have we created a smoothed border map? There's a simple reason for this, which is that we want the borders to be gradual instead of abrupt. Let's say we want rivers or streams between zones. This gradual border will allow us to progressively increase the depth of the river and making it look more natural in contrast with the adjacent zones.

All that's left is to flood each selected cell and apply that to a zone map.