Subscribe to our subreddit to get all the updates from the team!
Introduction
In our 3D game (miimii1205), we use a dynamically created navigation mesh to navigate onto a procedurally generated terrain. To do so, only the A* and string pulling algorithms were more specifically used until our last agile sprint. We recently added two new behaviors to the pathfinding : steering and wall collision avoidance. In this article, I will describe how I achieved a simple way for agents to not walk into walls.
Configuration
- 3D or 2D navigation mesh, as long as the 3D one is not cyclic.
- Navigation cells and their : polygonal edges, connections (other cell), shared edges (the line intersecting between two connected cells), centroids and normals.
- An A* and string pulled (not tested without string pulling) generated path consisting of waypoints on the navigation mesh.
The Algorithm
The agent is the pink low-poly humanoid and the final destination is the flag.
The ideal algorithm (yet unoptimized) would be to cast an oriented rectangle between each consecutive waypoint where its width is the two times the radius. Think of the agent's center position being in the middle of the width. Anyway, this algorithm is too complicated, too long to develop for our game, too big for nothing and so I thought about another algorithm, which has its drawbacks actually. However, it's more suited for our game.
Psss, check this article if you haven't seen it yet.
The algorithm is the following :
- For each waypoint, pick the current one and the next one until the next one is the last.
- Iterate over the current navigation cell's edges, which is defined by the agent's 3D position. To do that, you need a spatial and optimized way to determine the closest cell of a 3D point. Our way to do it is to first have have an octree to partition the navigation mesh. After that, get all the cells that are close to the point plus an extra buffer. To find the cell that is the closest to the point, for each picked cell, cast a projection of the position onto each one of them. This can be done using their centroids and normals. Don't forget to snap the projected position onto the cell. After, that compute the length of the resulting vector and pick the smallest one.
- Convert each edge to a 2D line by discarding the Y component (UP vector).
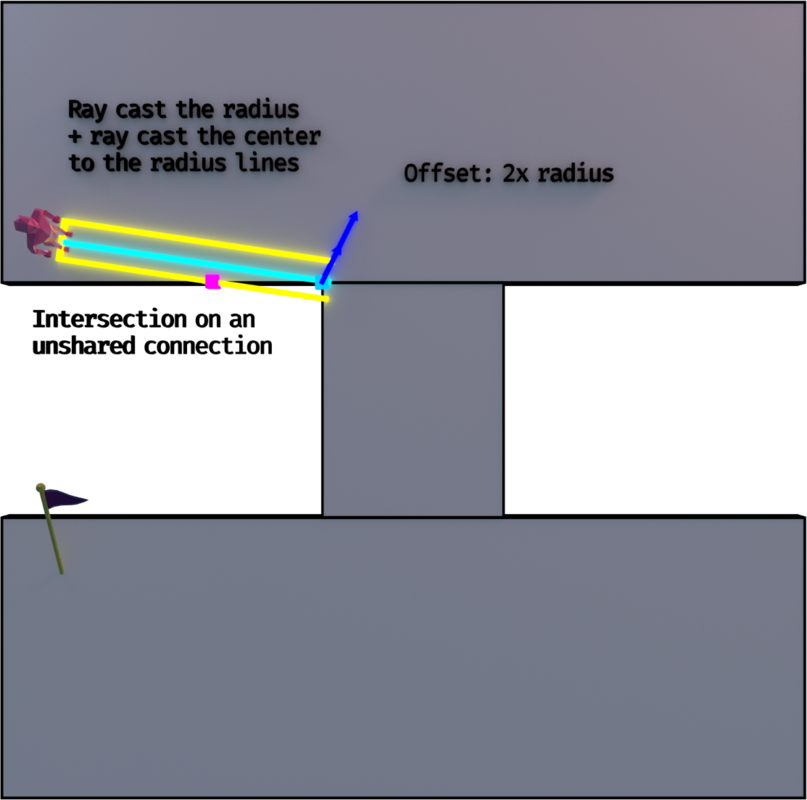
- For each side left and right, which are defined by the agent's position and direction towards the next waypoint, cast a 2D line that start from the agent's position, that goes towards one of the two perpendicular directions related to the direction to the next waypoint and that has a length of the defined radius.
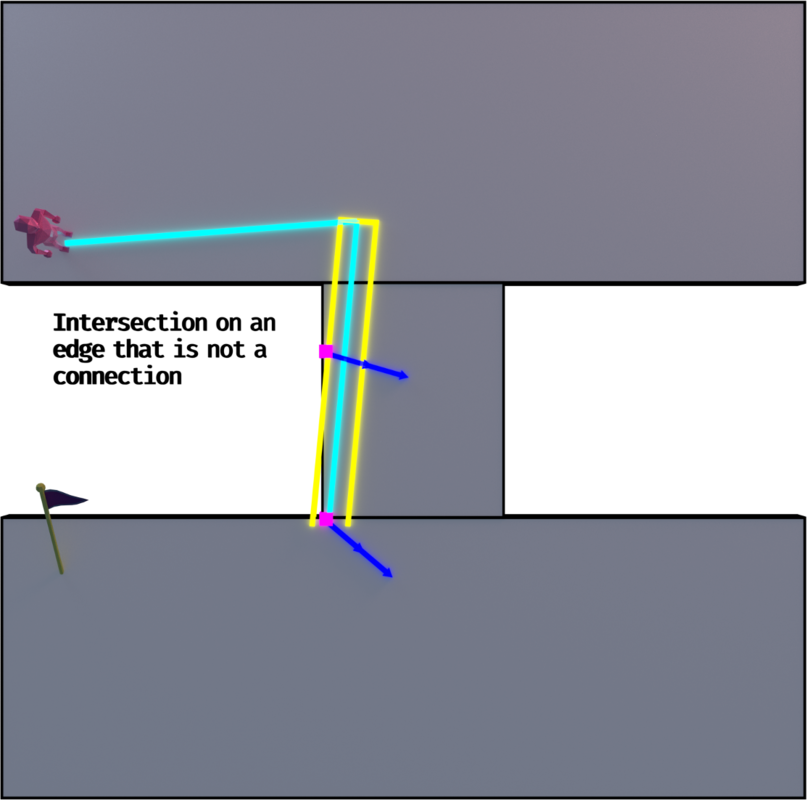
- If there's an intersection on a connection and that it's on the shared part of the connection, then continue with the connected cell's edges.
- If there are any intersections other than #5, create a new waypoint before the next waypoint. This new one's position is defined by the intersection's position translated by a length of two times the radius and projected towards the agent's current direction as a 2D line. The same translation is applied to the next waypoint.
- Cast two 2D lines, one on each side of the agent as described before, starting from the sides, going towards the same direction as the agent and of the same length between the current and next waypoint. Check for #5. If there is an intersection on a connection and that it's on the unshared part of the connection, then do #6 (no if). If there's an intersection on a simple edge, then translate the next waypoint as described in #6.
Here's a video of the algorithm in action :



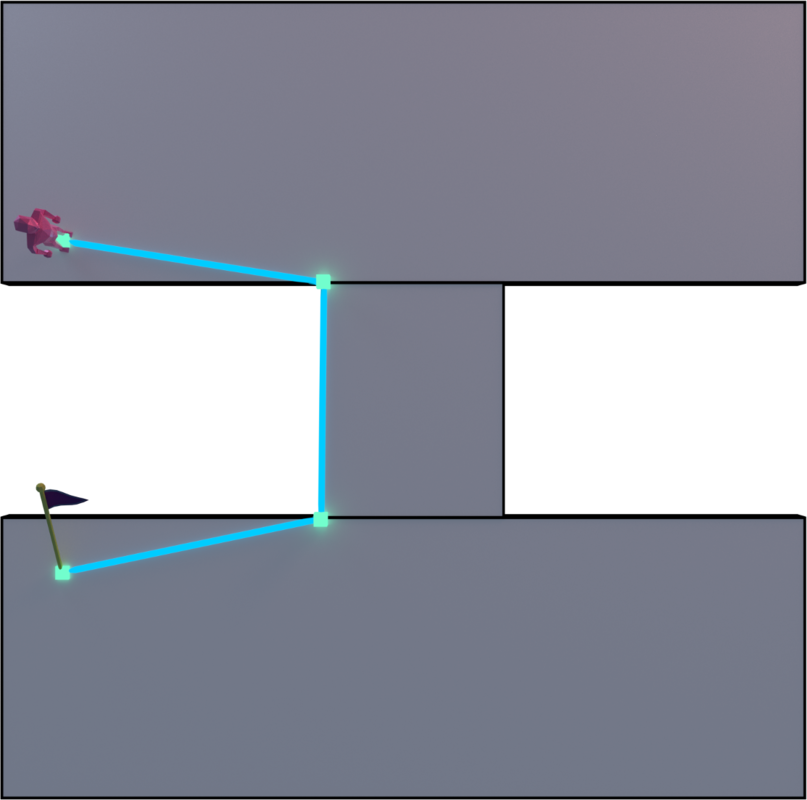
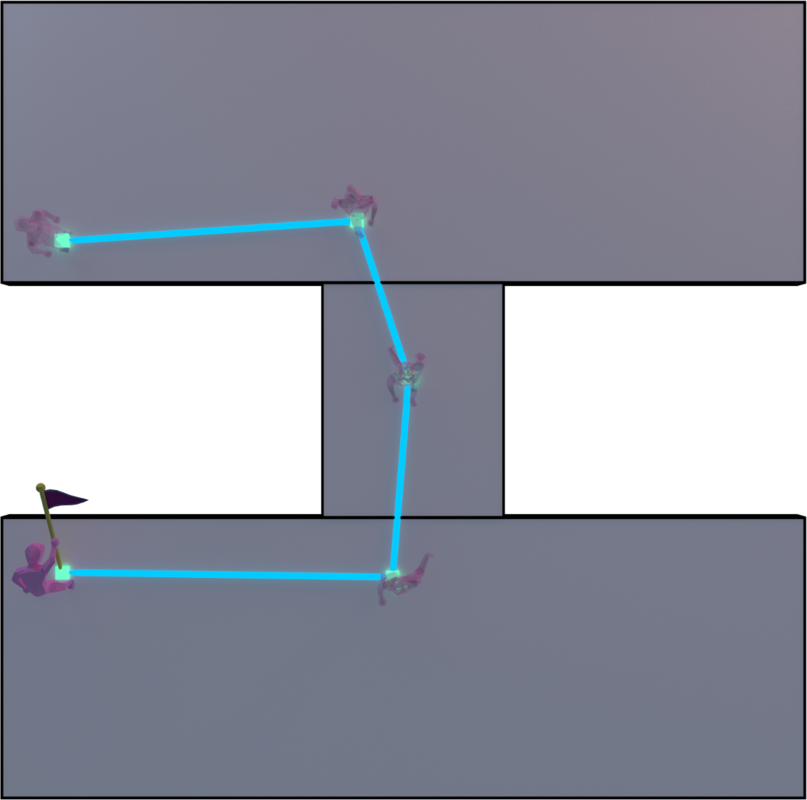




I feel like there has to be a simpler way to accomplish this. Can you make the corners have non-zero radius during string pulling? Or treat the corners as circles, and move the string-pulled lines to be tangent to the circles (plus an additional connecting chamfer)?