Oops I posted twice. Sorry.
SDL green flickering mess on nvidia Geforce GTX
I had to manually set the alpha channel to 8-bits on this combination of SDL and Geforce GTX. I did this right after calling SDL_Init(), before I call SDL_CreateWindow(). I didn't have to do this on the AMD GPU.
SDL_GL_SetAttribute(SDL_GL_CONTEXT_MAJOR_VERSION, 4);
SDL_GL_SetAttribute(SDL_GL_CONTEXT_MINOR_VERSION, 3);
SDL_GL_SetAttribute(SDL_GL_CONTEXT_PROFILE_MASK,
SDL_GL_CONTEXT_PROFILE_COMPATIBILITY);
SDL_GL_SetAttribute(SDL_GL_RED_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_GREEN_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_BLUE_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_ALPHA_SIZE, 8); // Must set this manually!!!
SDL_GL_SetAttribute(SDL_GL_DEPTH_SIZE, 16);
SDL_GL_SetAttribute(SDL_GL_DOUBLEBUFFER, 1);
@JoeJ My computer has only 8GB of RAM. I don't know anything about timeouts. Perhaps I'm not dealing with a large number of data, more than 8GB.
taby said:
Perhaps I'm not dealing with a large number of data
The fractal is very high resolution, and i guess you first make a density volume, then marching cubes?
So the volume must be huge? Though, i just remember, i think you always process a 2D slice of the volume, so you never need the whole volume?
I do something similar. Just using volume blocks instead slices.
Timeouts happen if a GPU task takes too long, maybe 100 ms or a second. In such case the driver terminates the task and your application crashes.
I get this if i try to render many triangles. Surely some bug related to Vulkan. I hope to find it occasionally one day…
(I'm glad you did not reinstall Windows to fix your issue ;D )
You are correct. I only use two adjacent xy slices at a time, which is what I use to generate the triangles by using Marching Cubes. Generally, I use a resolution of 1000x1000x1000 for large meshes / screenshots. I also use isobands, as you can see. Paul Bourke was the one who showed me this visualization trick (I came up with my own code to do it though).
The Marching Cubes code is at:
It should be noted that I use the standard vertex interpolation function.
You can set the equation at:
Yep, thankfully I didn't need to reinstall drivers, or Windows! ?
Sorry that I can't be of help regarding your Vulkan apps.
JoeJ said
Timeouts happen if a GPU task takes too long, maybe 100 ms or a second. In such case the driver terminates the task and your application crashes.
I finally fixed a bug that caused my quaternion Julia set code to barf on nvidia GPUs. In the following code, I generate a vector<bool> for the whole volume, and then do custom vertex interpolation for Marching Cubes. This is all on the GPU, using OpenGL 2. Maybe you can see if OpenGL has timeouts.
https://github.com/sjhalayka/qjs-isosurface
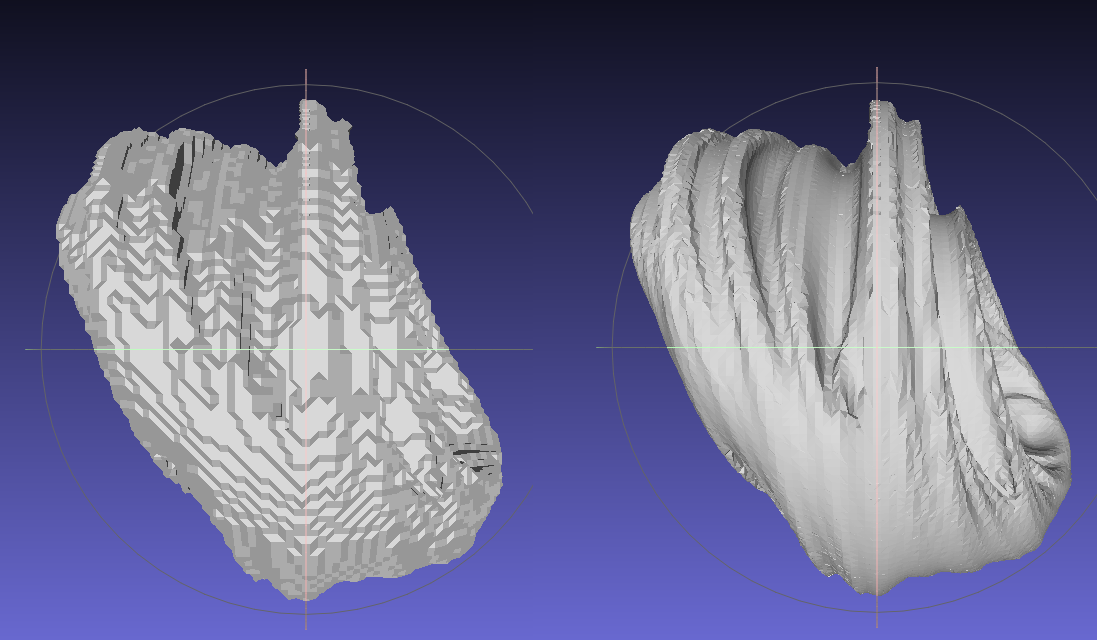
The results speak for themselves (on the left I use no refinement steps, and on the right I use 8 refinement steps):
taby said:
Maybe you can see if OpenGL has timeouts.
If you never experienced them, don't worry.
Imagine you have a infinite loop in a shader, and it should run forever. In such case the driver terminates after a certain time spent on the same dispatch, the app crashes, but the user gains back control over the computer.
So you can make an infinite loop to see this happening and what error popup the driver usually shows.
taby said:
The results speak for themselves (on the left I use no refinement steps, and on the right I use 8 refinement steps):
I wonder how you implement the refinement, but using binary voxels is worst case for iso surface extraction. Ideally we want density (i guess impossible for fractals), or distance (approximations are possible).
To support meshes, i use binary voxelization at very high resolution too. Then i convert a 4^3 block of voxels to a single density value, so basically i do multi sampling to get a density range of 64 gradual values. That's ok.
Unfortunately i realized too late that the binary voxelization (although higher resolution) is completely useless to me. Actually i store DAG compressed binary voxel volumes on disk, although using just the density would give me much better compression ratios.
Using the density volume we get a smooth isosurface in the first step, which would help against the quantization issues in your picture. Ofc. you'd need to evaluate the fractal N times per cell for multi sampling, so the cost is very high.
However, with approximated distance the cost would be still low. So this would be ideal to voxelize fractals.
Programs like Mandelbuld3D use distance estimation to render the fractals using sphere tracing, so the same tracing algorithm which is used in UE5 Lumen for example.
And from that i found distance formulas on fractal forums.
But unfortunately, for tracing you only need positive distance (from the outside of the model), but no negative distance (from the inside). So their formulas lack negative distance calculation, and we can't use them for volume based methods.
That's where my trial to support fractals has ended so far. I'd need to learn how their distance estimators work to add the missing pieces. Multi sampling isn't practical for me, as editing the scene would become too slow.
Actually, the magnitude of the Z quaternion, post-iteration, stands in as the density, and the isosurface is where the magnitude equals the threshold value. Alan Norton told me about that a decade or two ago. There is no sub-sampling involved, like I had initially thought too.
The refinement is still needed when one uses the magnitude as the density. True, it does not look as bad as that generated by a boolean field alone, like on the left, but it still needs refinement to look great.
Thanks for listing all of those technologies that I might be interested in. I'll take a look!
The refinement code is:
int lessthan(vec4 left, vec4 right)
{
if(left.x < right.x)
return 1;
else if(left.x > right.x)
return 0;
if(left.y < right.y)
return 1;
else if(left.y > right.y)
return 0;
if(left.z < right.z)
return 1;
else if(left.z > right.z)
return 0;
return 0;
}
vec3 vertex_interp(vec4 v0, vec4 v1)
{
// Sort the vertices to fix cracks that would otherwise occur
if(0 == lessthan(v0, v1))
{
vec4 temp = v0;
v0 = v1;
v1 = temp;
}
// Start half-way between the vertices.
vec3 result = (v0.xyz + v1.xyz)*0.5;
// Refine the result, if need be.
if(0 < vertex_refinement_steps)
{
vec3 forward, backward;
// If v0 is outside of the surface and v1 is inside of the surface ...
if(v0.w > v1.w)
{
forward = v0.xyz;
backward = v1.xyz;
}
else
{
forward = v1.xyz;
backward = v0.xyz;
}
for(int i = 0; i < vertex_refinement_steps; i++)
{
// If point is in the quaternion Julia set,
// then move forward by 1/2 of a step,
// else move backward by 1/2 of a step ...
if(threshold > iterate(vec4(result.xyz, z_w)))
{
backward = result;
result += (forward - result)*0.5;
}
else
{
forward = result;
result += (backward - result)*0.5;
}
}
}
return result;
}This is in contrast to the linear interpolation done using Paul Bourke's original code for the CPU.
P.S. I generate the entire Boolean field, in order to easily add blocks, subtract blocks, and make the sculpture hollow. The result is perfect for 3D printing! Here we see that I added a block at the bottom, to serve as the base of the sculpture.









