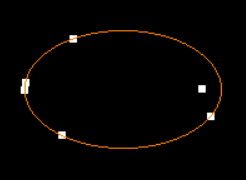
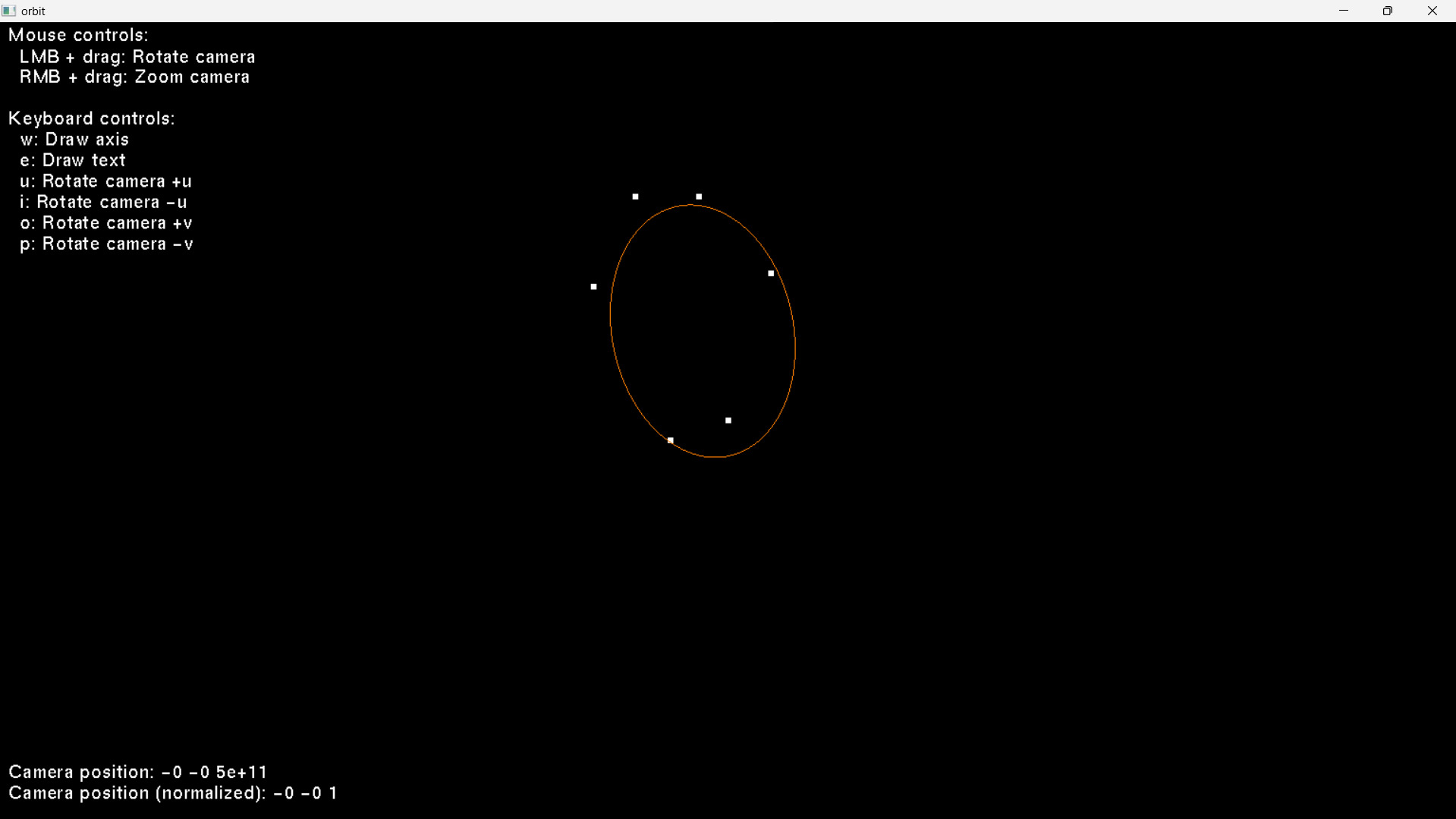
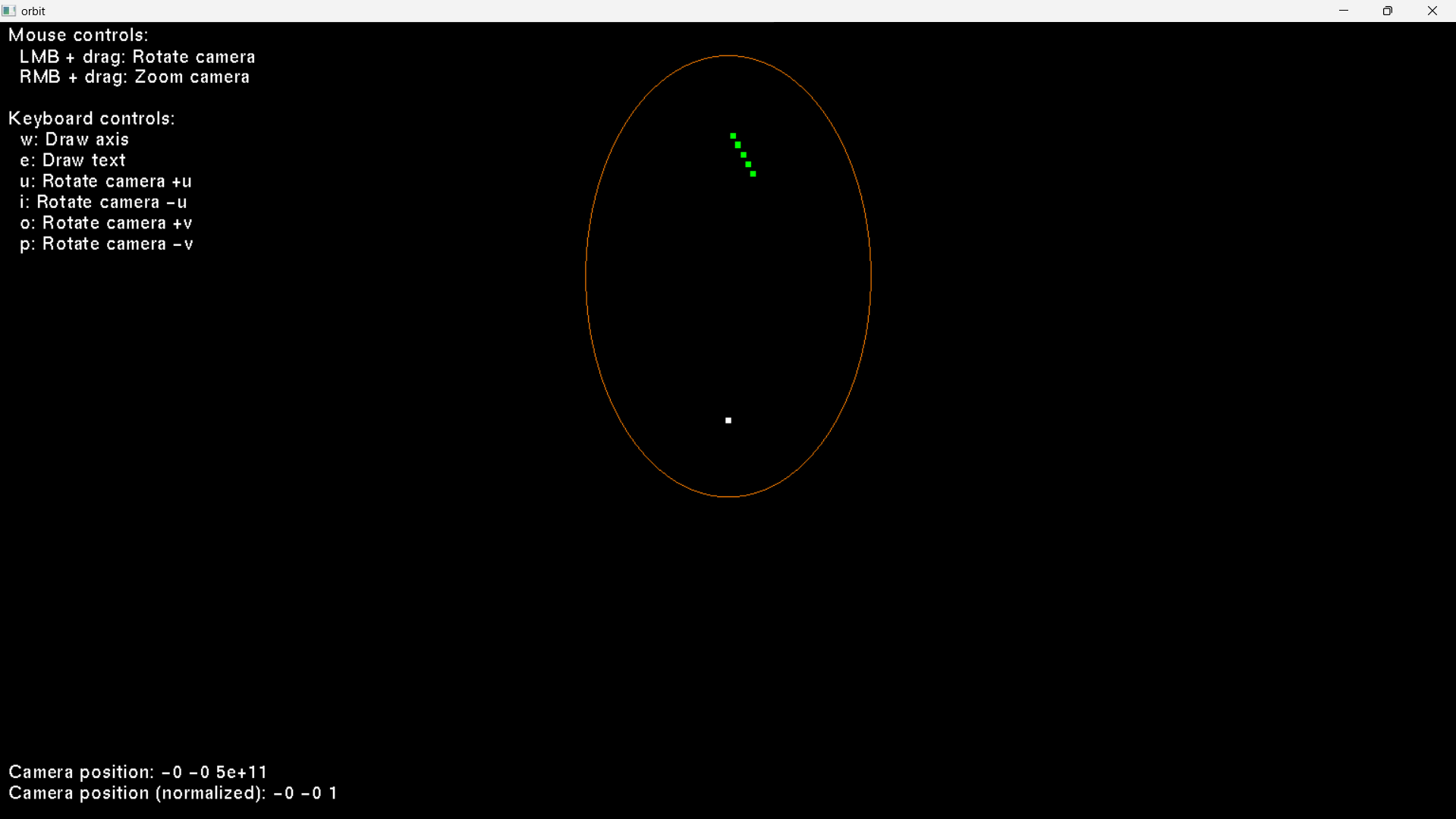
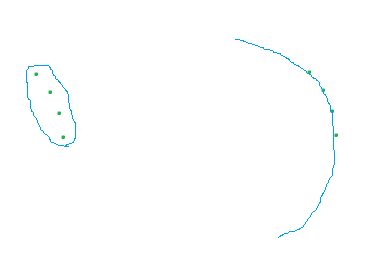
I am trying to fit an ellipse to some points along an orbit. The full code is at: https://github.com/sjhalayka/ellipse_fitting

As you can see, it sort of works, but not quite, especially where there are a lot of input points:

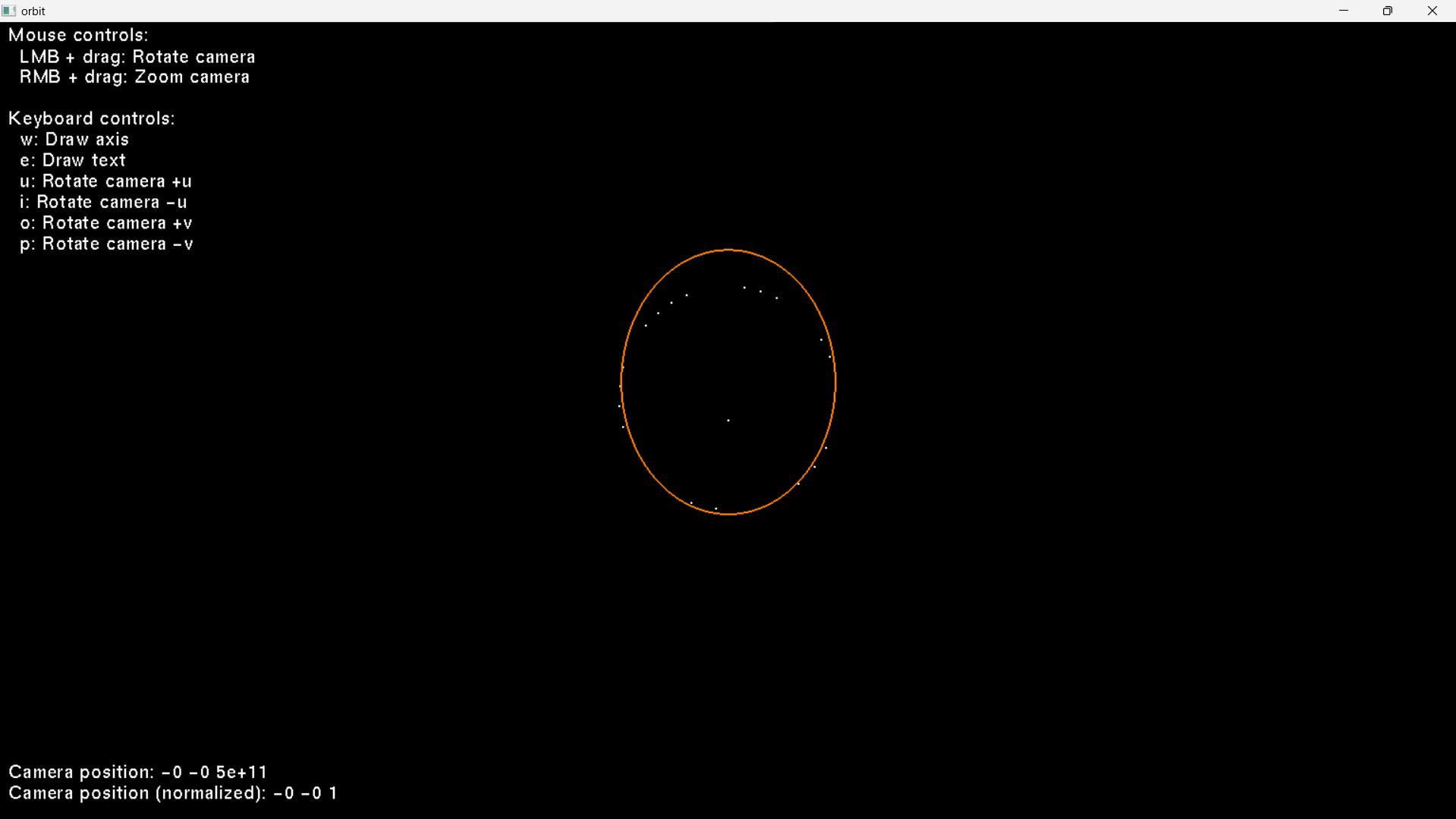
Here is the relevant code:

void idle_func(void)
{
	static size_t frame_count = 0;

	frame_count++;

	const double dt = 10000; // 10000 seconds == 2.77777 hours

	proceed_symplectic4(mercury_pos, mercury_vel, grav_constant, dt);

	positions.push_back(mercury_pos);

	static bool calculated_ellipse = false;

	if (calculated_ellipse == false && frame_count % 123 == 0)
		ellipse_positions.push_back(positions[positions.size() - 1]);

	if (false == calculated_ellipse && ellipse_positions.size() == 20)
	{
		calculated_ellipse = true;

		double largest_distance = 0;

		for (size_t i = 0; i < ellipse_positions.size(); i++)
			if (ellipse_positions[i].length() > largest_distance)
				largest_distance = ellipse_positions[i].length();

		global_ep.centerX = 0;
		global_ep.centerY = 0;
		global_ep.semiMajor = 10 * largest_distance;
		global_ep.semiMinor = 10 * largest_distance;

		double global_total_error = DBL_MAX;

		for (size_t i = 1; i < 10000; i++)
		{
			EllipseParameters local_ep;

			local_ep.centerX = global_ep.centerX;
			local_ep.centerY = global_ep.centerY;

			if (i % 2 == 0)
			{
				local_ep.semiMajor = global_ep.semiMajor;
				local_ep.semiMinor = global_ep.semiMinor * 0.9;
			}
			else
			{
				local_ep.semiMajor = global_ep.semiMajor * 0.9;
				local_ep.semiMinor = global_ep.semiMinor;
			}

			double local_total_error = 0;

			for (size_t j = 0; j < ellipse_positions.size(); j++)
				local_total_error += abs((ellipse_positions[j].x * ellipse_positions[j].x / (local_ep.semiMinor * local_ep.semiMinor)) + (ellipse_positions[j].y * ellipse_positions[j].y / (local_ep.semiMajor * local_ep.semiMajor)) - 1.0);

			if (local_total_error < global_total_error)
			{
				global_ep.centerX = 0;
				global_ep.centerY = 0.5*calculateFoci(local_ep).focus1X;
				global_ep.semiMajor = local_ep.semiMajor;
				global_ep.semiMinor = local_ep.semiMinor;

				global_total_error = local_total_error;
			}
		}
	}

	glutPostRedisplay();
}

Any glaring errors in logic that I'm missing?

taby said:
Any glaring errors in logic that I'm missing?

I guess your code assumes the ellipse to be axis aligned?
If you would rotate your input points 45 degrees, would you get the same output but rotated 45 degrees as well?

Here's what i would do:
Calculate the average of all points and make it the center of the ellipse.
Calculate the line best fitting the point distribution and make it the longer axis of the ellipse.
The shorter axis is simply the perpendicular line.
Knowing both axis and thus the orientation of the ellipse, we can now measure the radi by summing up point distribution along those axis.

In 2D i would use complex numbers raised to the power of two to fit the line.
In 3D i would use covariance matrix and singular value decomposition to find orthogonal axis.

However, my proposal assumes your points are distributed with uniform density across the whole surface (or volume) of the ellipse / ellipsoid.
If your input covers only a small path of a larger ellipse for example, my proposals would fail and you need something else.

I think i saw related tools here: https://github.com/HRI-EU/WildMagic5p17/tree/master/LibMathematics/Approximation

I got it to work. Yes it takes rotation into account. I answered the question on Physics StackExchange.

P.S. Grok, Claude, and ChatGPT all had errors in the code. AI is shit.

Arbitrary rotation works… sort of ok.

taby said:
P.S. Grok, Claude, and ChatGPT all had errors in the code. AI is shit.

I still have not used such tools and can't tell.
I see lots of ‘X, but made in the 50's’ video suggestions on YT. Quite impressive. Once this can generate assets for games, well… Nintendo will change their mind.
And they are very close:

(Reminds me a bit on my own work - i knew remeshing volume data would work well for AI)

I also took the bait with AI music. My favorite:

I did not know this is AI. I started to speculate pretty quickly, but anyway: I liked it.
Then i found there is countless of similar stuff, and yes - it's all AI. Imaginary Band names, years, and album covers.

I've created thousands of album covers i guess. And i can tell you: I have seen covers much worse than those, including my own.

And i know enough about music to judge that too. It's low quality, imperfect, sometimes just wrong.
But it's the best ‘progressive rock’ album i've heard in years. The compositions are creative and interesting, and it sounds fresh and like something new.

So, you don't get away with just saying ‘AI is shit’. It's not. It has obvious skills. Maybe those skills are never exactly what the ‘creator’ wants, but without doubt it shows creativity and talent.
It can extract those skills from the training data. It sees other patterns than humans do.

And then it spits something out which can be useful, e.g. to serve the growing content addiction of a future generation of humans, which then are all ‘creators’. They can no longer play the guitar or paint an image themselves, but they can express their desire with words, and the machine makes it real for them, ready to be consumed.

However, to keep the ball rolling, the machinery needs food. It needs new data. It can not recycle itself, because then quality decreases, and the consumers are no longer happy. They might revolt against the system. This shall not happen.
To avoid the collapse, the system rewards an elite of human artists. They become idols, super rich, and they feed their creativity directly into the machine. They have mechanical hands with 20 fingers to play guitar faster than Yngwie, and shiny headsets to extract all their thoughts.

Hehehe, cyberpunk is now. And nothing really changes. : )

I am being half-joking when I call AI a bad name. It's impressive how well it works in general. However, it is also impressive how well the different models all stole the same shit code that didn't work at all. LOL

JoeJ – I've had a change of heart. I'm in love with the AIs, now that I've spent a week using them to fool around with ellipse fitting. I've tried Copilot, ChatGPT, Grok, and Claude – my favourite.

There's a lot of example code that solves for the linear ellipse coefficients, using Jacobi SVD for example. I managed to stumble upon a different method, using gradient descent, but I'm still having small problems though.

It works, almost. The main problem is that it erroneously places the orbiting body at one of the foci.

Any glaring problems with the code? It's gotta be something simple, but a solution eludes me for now.

struct Point {
	double x, y, vx, vy;
};

// Helper function for distance calculation
double distance(double x1, double y1, double x2, double y2) {
    return sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2));
}

// Objective function for optimization (least squares)
double objectiveFunction(const VectorXd& params, const vector<Point>& points, const Point& focus) {
    double h = params[0], k = params[1], a = params[2], b = params[3];
    double error = 0;
  
	for (const auto& p : points)
	{
        double dist1 = distance(p.x, p.y, h, k);
        double dist2 = distance(p.x, p.y, focus.x, focus.y);
        error += pow(dist1 + dist2 - 2 * a, 2); // Distance condition
        
        // Since we're axis-aligned, we simplify velocity condition:
        // Velocity should be more in line with the axis of the ellipse
        double velError = 0;

        if (abs(p.vx) > abs(p.vy)) 
		{ // Suggesting a is along x
			velError = pow(p.vy / p.vx - (k - p.y) / (h - p.x), 2); // Check alignment with y
        }
		else
		{
			velError = pow(p.vx / p.vy - (h - p.x) / (k - p.y), 2); // Check alignment with x
        }

        error += velError;
    }

    return error;
}

// Simple solver function using gradient descent (for demonstration)
VectorXd solveEllipseParameters(const vector<Point>& points, const Point& focus) 
{
    VectorXd params(4); // h, k, a, b

	vector<double> mvec;
	mvec.push_back(max(abs(points[0].x), abs(points[0].y)));
	mvec.push_back(max(abs(points[1].x), abs(points[1].y)));
	mvec.push_back(max(abs(points[2].x), abs(points[2].y)));
	mvec.push_back(max(abs(points[3].x), abs(points[3].y)));
	mvec.push_back(max(abs(points[4].x), abs(points[4].y)));

	sort(mvec.begin(), mvec.end());

	double m = mvec[4];
	
    params << m*0.5, m * 0.5, m * 0.5, m * 0.5; // Initial guess

    int iterations = 100000;
    double stepSize = 0.00001;

    for (int i = 0; i < iterations; ++i) {
        VectorXd gradient = VectorXd::Zero(4);
        for (int j = 0; j < 4; ++j) {
            VectorXd paramsPlus = params;
            paramsPlus[j] += stepSize;
            VectorXd paramsMinus = params;
            paramsMinus[j] -= stepSize;
            
            gradient[j] = (objectiveFunction(paramsPlus, points, focus) - objectiveFunction(paramsMinus, points, focus)) / (2 * stepSize);
        }
        params -= stepSize * gradient;
    }

    return params;
}

…

vector<Point> points;
	
Point point0(orbit_points[0].x, orbit_points[0].y, orbit_velocities[0].x, orbit_velocities[0].y);
Point point1(orbit_points[1].x, orbit_points[1].y, orbit_velocities[1].x, orbit_velocities[1].y);
Point point2(orbit_points[2].x, orbit_points[2].y, orbit_velocities[2].x, orbit_velocities[2].y);
Point point3(orbit_points[3].x, orbit_points[3].y, orbit_velocities[3].x, orbit_velocities[3].y);
Point point4(orbit_points[4].x, orbit_points[4].y, orbit_velocities[4].x, orbit_velocities[4].y);
		
points.push_back(point0);
points.push_back(point1);
points.push_back(point2);
points.push_back(point3);
points.push_back(point4);

Point focus = { 0, 0 };

VectorXd params = solveEllipseParameters(points, focus);

double h = params[0], k = params[1], a = params[2], b = params[3];

global_ep.angle = 0;
global_ep.centerX = 0;
global_ep.centerY = k;
global_ep.semiMajor = a;
global_ep.semiMinor = b;

cout << global_ep.angle << endl;
cout << global_ep.centerX << endl;
cout << global_ep.centerY << endl;
cout << global_ep.semiMajor << endl;
cout << global_ep.semiMinor << endl;

taby said:
It works, almost. The main problem is that it erroneously places the orbiting body at one of the foci.

In the picture the green points are either a line, or a small segment of a large ellipse.
For such data i would hope Dave Eberlys codebase from the link has a fitting function which works.

But in the first picture you have posted the points are more like a dsitribution of density, and my proposal of using SVD would match an ellpsoid to represent this distribution, similar to the inertia tensor used in physics simulation.

My SVD idea is somewhat different than the one you use with Eigen library. I see you give it per point data wich reminds on leat squares methods, but i don't need such data. In 3D space, i would accumulate 3x3 covariance matrix from all points, then doing SVD on that.
However, the result of my method would look very similar to what you show in the first 3 images.

I don't know much about curve fitting, but surely you would need to pick different methods, depending on what your given points typically look like.

A picture of what i mean:

Left is expected result from density SVD, right is curve fitting.
I guess you need to decide for the better method depending on your data.