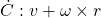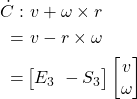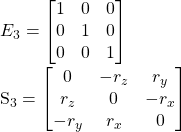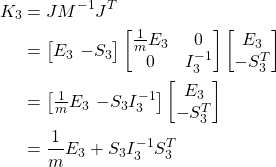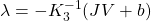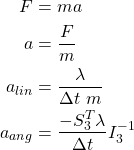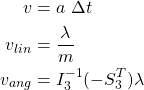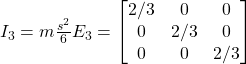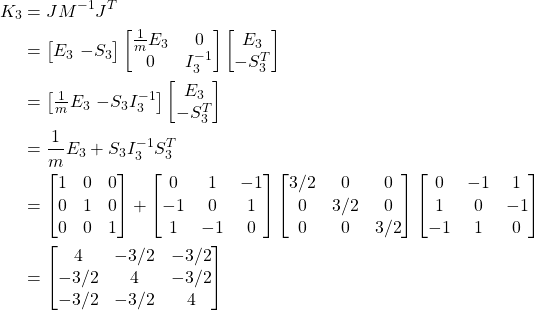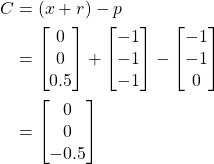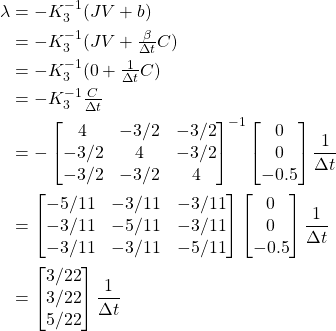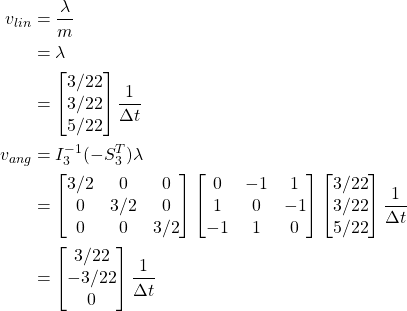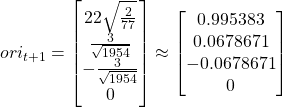I'm trying to implement an impulse based constraint solver for the case of a 3D cube falling onto a horizontal plane. When a vertex of the box is below the plane, I'm solving the constraint where the vertex of the box should be anchored to the contact point on the plane i.e. a ball and socket joint.
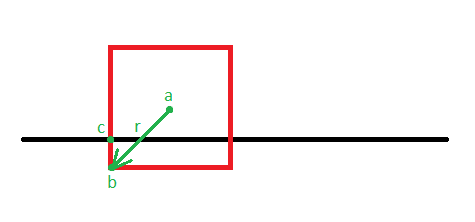
In this example I'm solving the constraint where b - c = 0. Since my constraint solver works at the velocity level, the idea here is that I'm applying an impulse to the cube at point b. This will both move the cube upwards and induce a rotation. Also, there is no restitution involved.
I'm trying to gain an intuitive understanding about whether my solver is working correctly or not. If I set the baumgarte stabilization coefficient to 1 such that the constraint is completely satisfied in one run of the solver then the cube should move & rotate such that b - c = 0 right? The problem I'm having is that this is not happening.

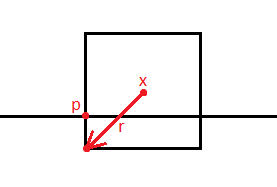
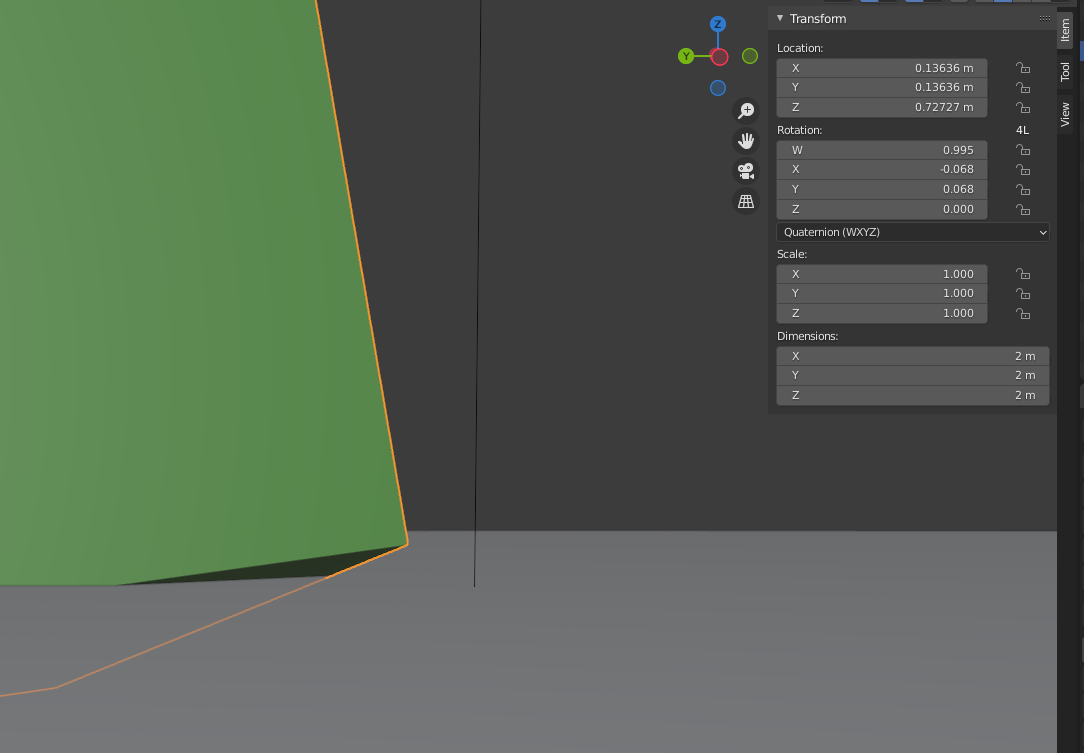
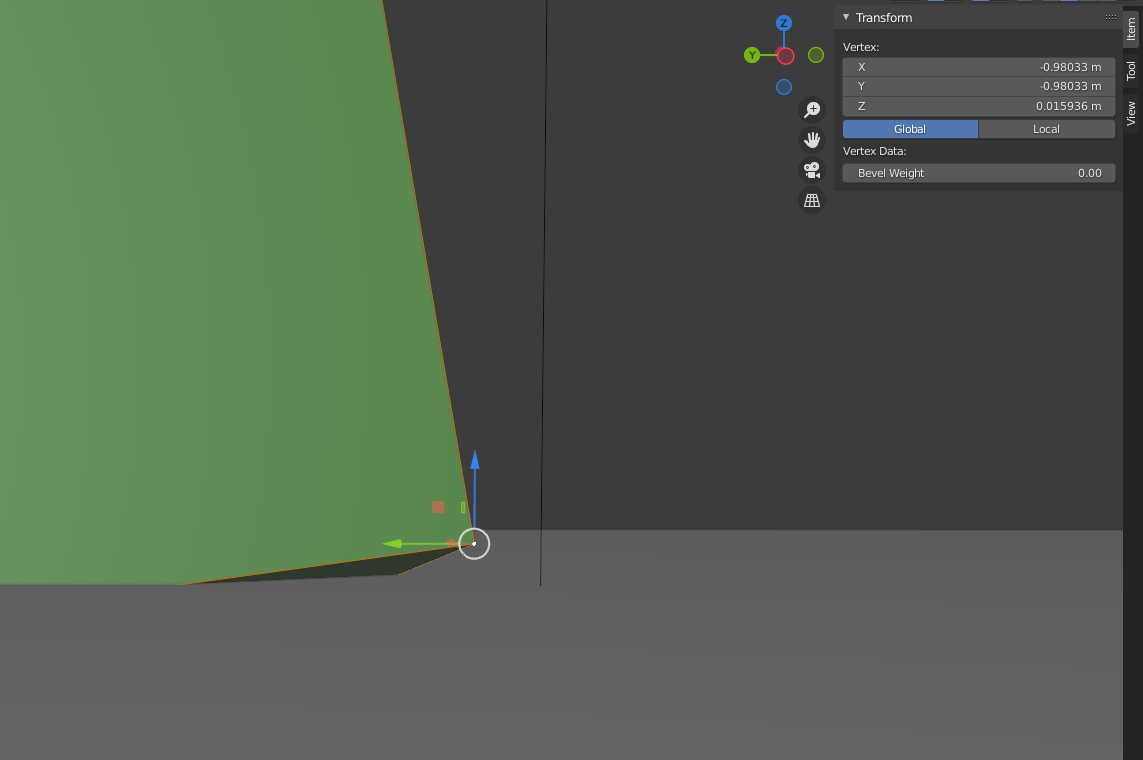
The point where the red line intersects the plane would be point c in the first diagram and the corner of the cube would be point b. This is the result of solving the constraint once with a baumgarte stabilization coefficient of 1, in that case is this correct? I don't think it is since b is not equal to c but I've checked the math and I cannot find a mistake. Because the math is so complicated, before I share any of the code which calculates the impulse is the assumption correct that these two points should be equal? Should the direction of the impulse be completely vertical? Or is it expected that it would have some non zero horizontal values to account for the rotation applied to the box?
Here is a breakdown of the code.
// integrate linear and angular velocity
box.velocity += ...;
box.angular_velocity += ...;
// integrate position and rotation
box.position += box.velocity * delta_time;
let w = Quaternion::new(box.angular_velocity.x, box.angular_velocity.y, box.angular_velocity.z, 0.0);
box.orientation += w * box.orientation * 0.5 * delta_time;
box.orientation.normalize();
if box vertex is below plane {
// calculate force required to solve the constraint
let f_linear = ...;
let f_angular = ...;
// integrate linear and angular velocity
box.velocity += (1.0 / mass) * f_linear;
box.angular_velocity += inertia_tensor_inverse * f_angular;
// integrate position and rotation
box.position += box.velocity * delta_time;
let w = Quaternion::new(box.angular_velocity.x, box.angular_velocity.y, box.angular_velocity.z, 0.0);
box.orientation += w * box.orientation * 0.5 * delta_time;
box.orientation.normalize();
}