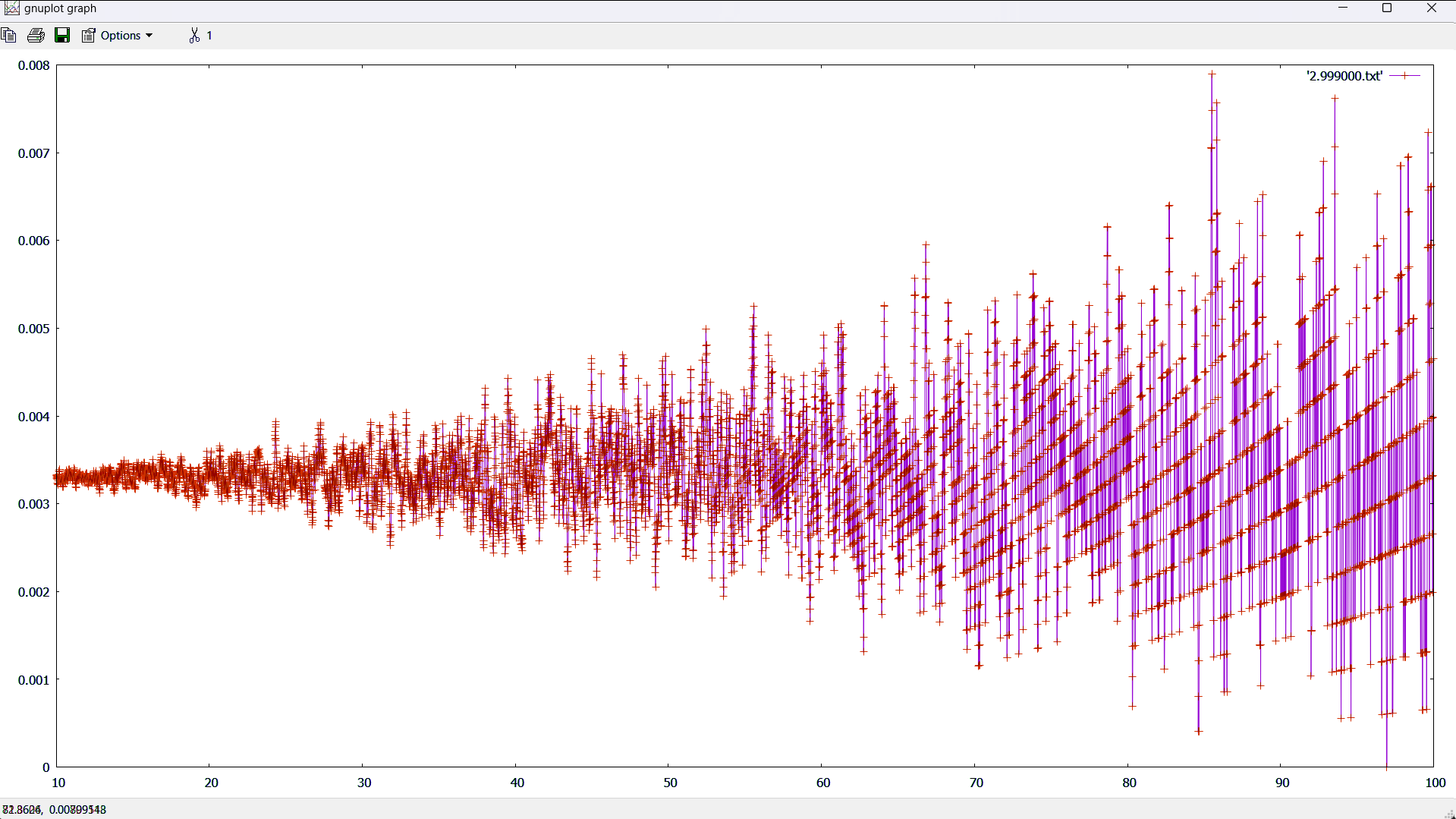
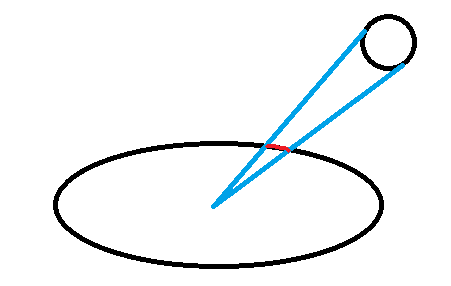
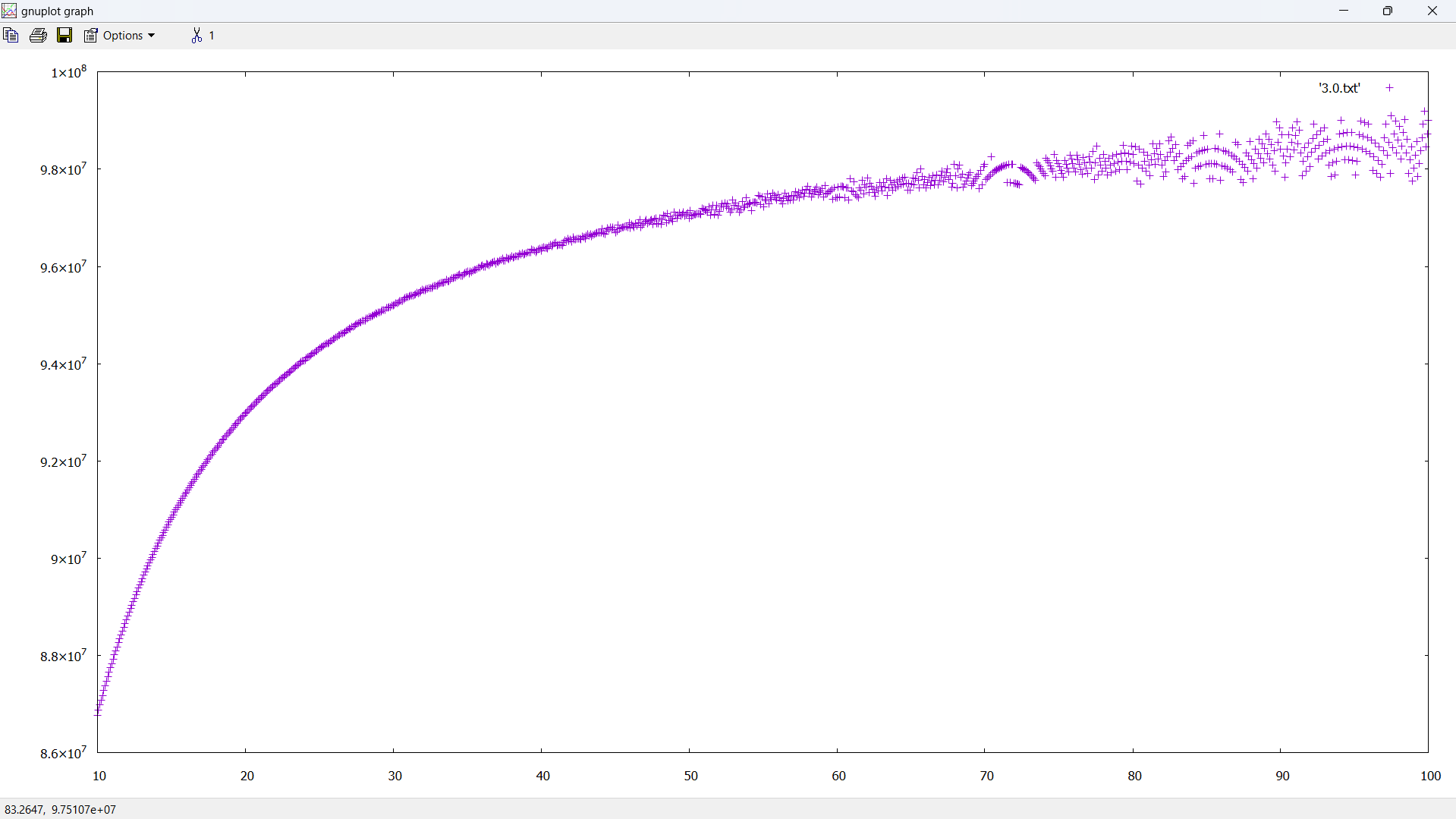
I am only thinking of this in terms of physics because the code reproduces Newtonian gravity (e.g. D = 3.0), where the acceleration is relatively small. In terms of geometry, I'm trying everything that I can think of to hammer out the widening of the bands. The bands, if not widening, are obviously the result of discrete steps, which is totally expected. However, the gradient reduces as distance increases, at an accelerating rate (the bands are curves in general). For fun, I set epsilon to 1 and it makes no difference.
const long long signed int collision_count_plus = get_intersecting_line_count(receiver_pos_plus, 1.0, D, true);
const long long signed int collision_count = get_intersecting_line_count(receiver_pos, 1.0, D, true);
vector_3 gradient;
gradient.x = static_cast<MyBig>(collision_count_plus - collision_count) / epsilon;I don't quite understand what your two images are showing. Can you please elaborate?