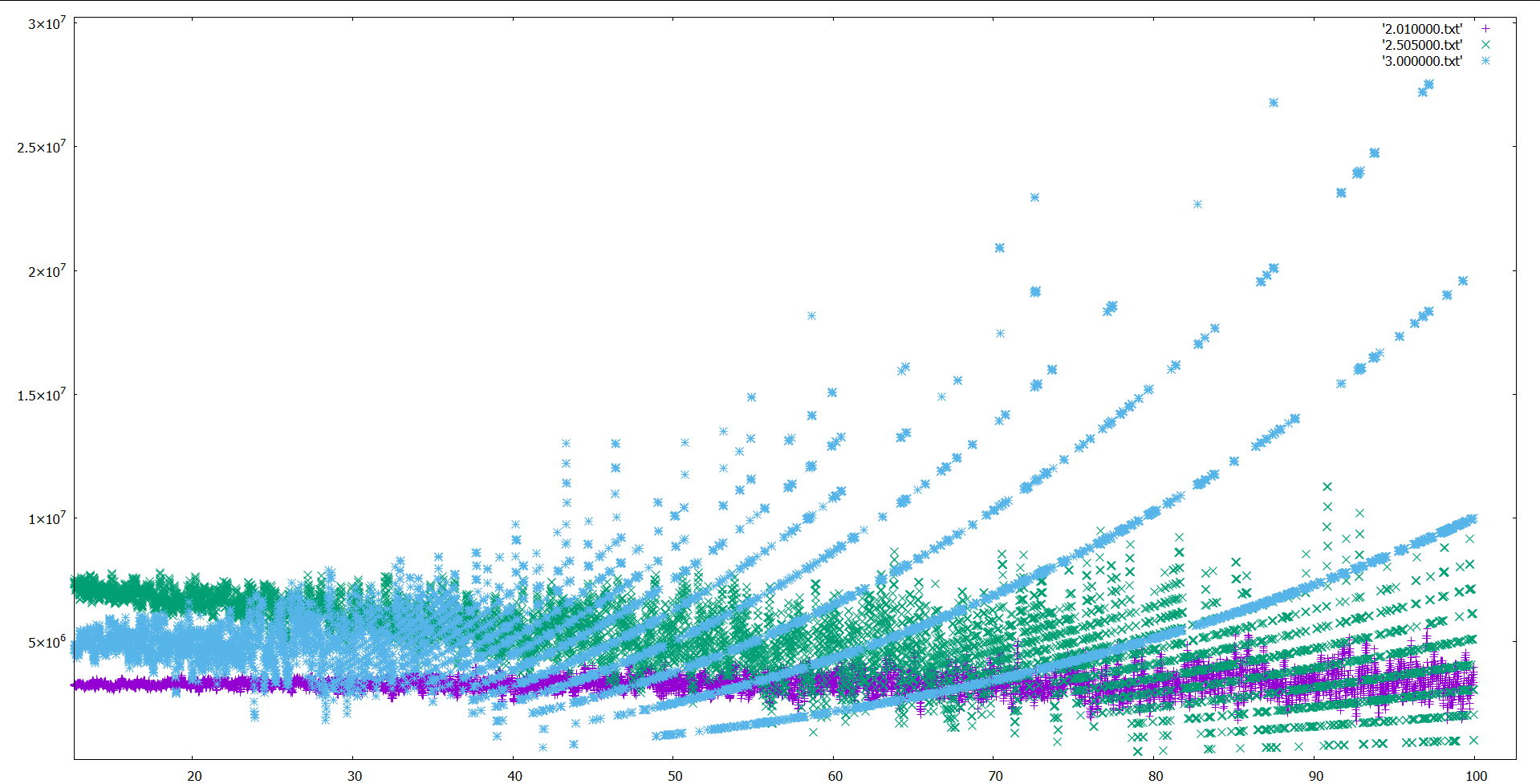
Here is the diagram for dimension D = 2.01, D = 2.5, D = 3.
I am currently waiting on the calculations using Boost Multiprecision. Hopefully the slow down will be offset by better plots.
I gave up on Boost Multiprecision. There's actually no need for it. long double is fine.
The behaviour that we were trying to describe (the bands) are not because of fp precision, but rather because of the number of intersections we were obtaining.
The greater the number of intersections, the more bands there are.
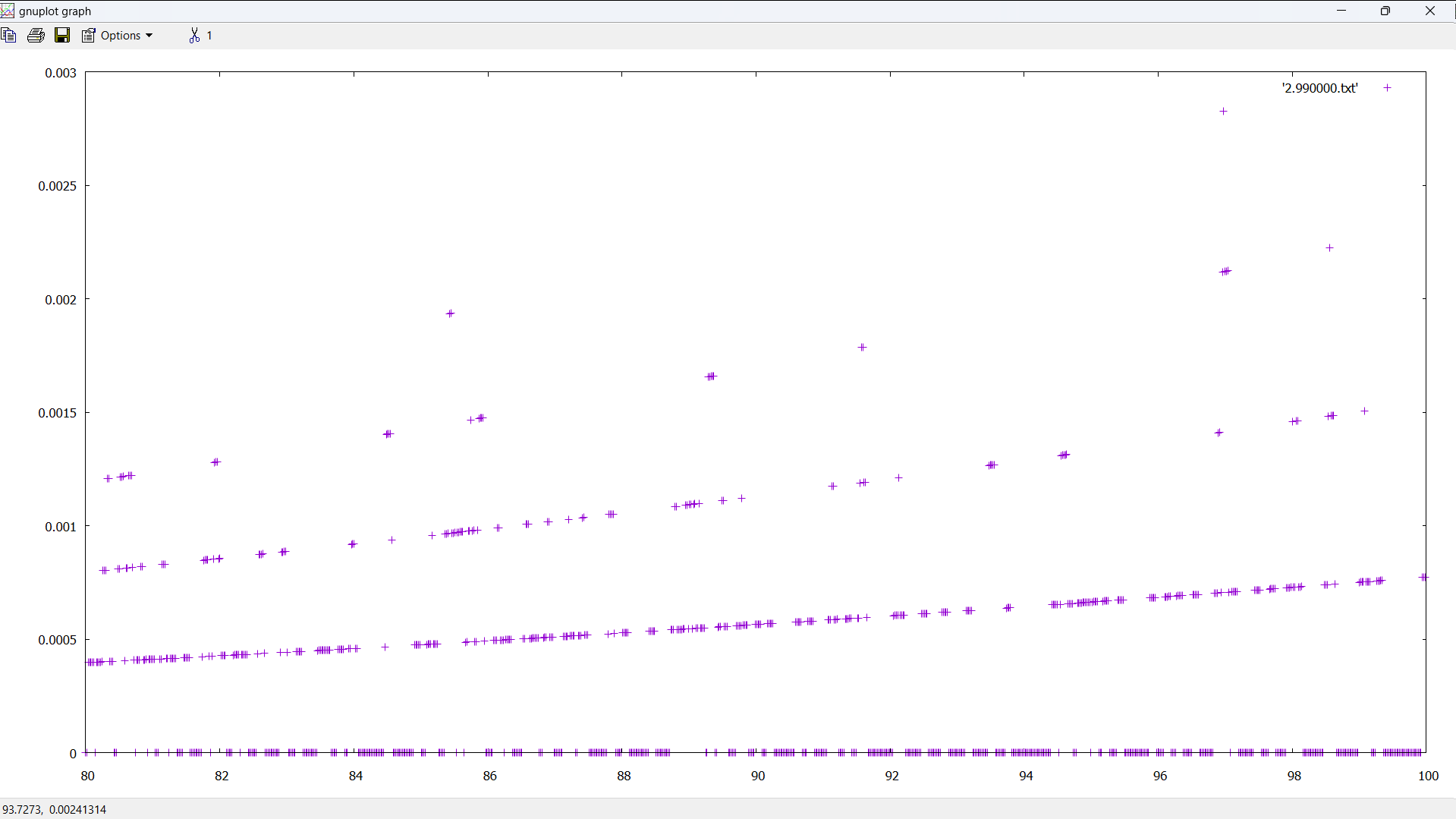
Where n = 10,000,000:
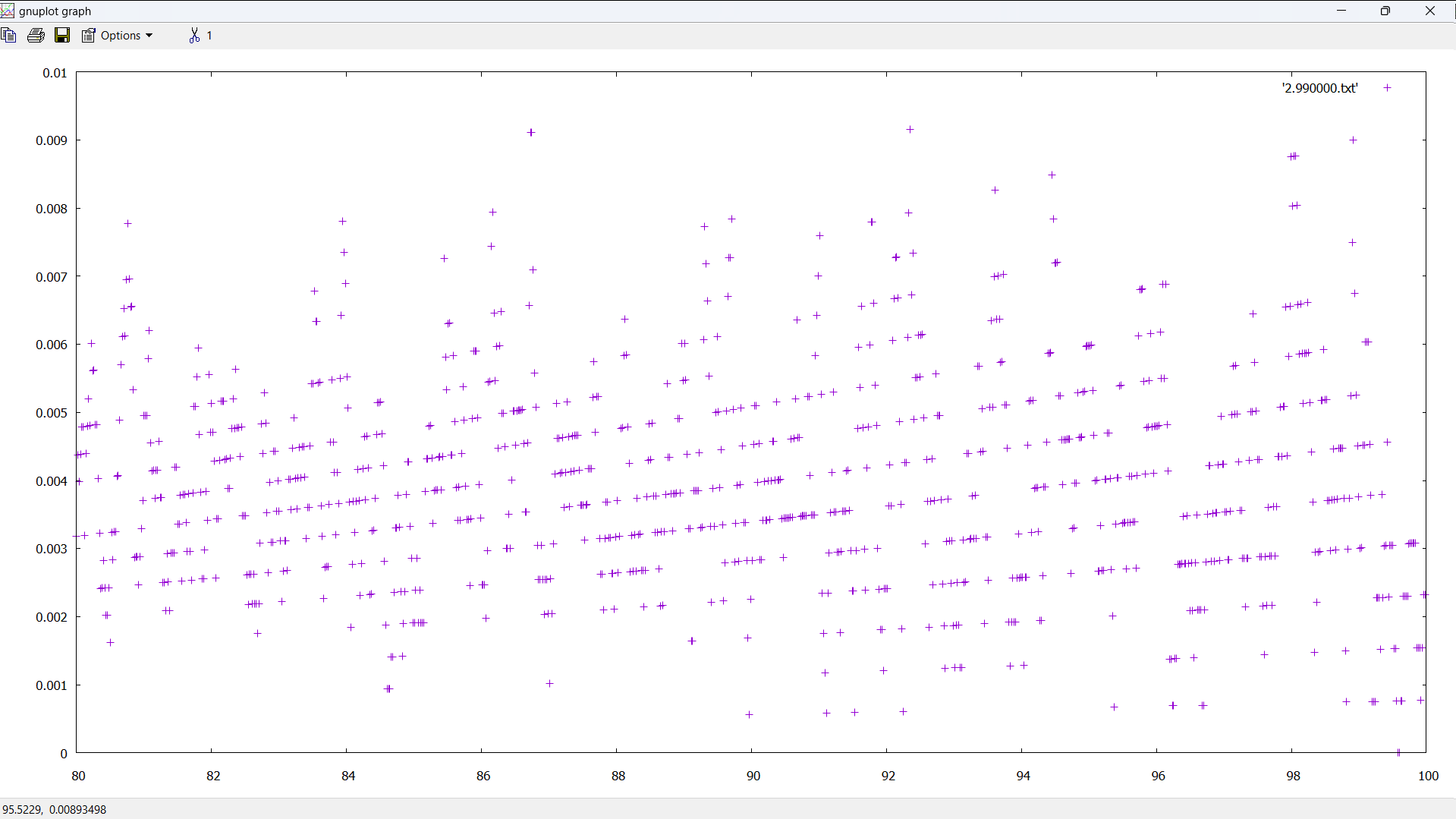
Where n = 100,000,000:
So the universe has banding artifacts. Fine. If so, i no longer have to fix them as they appear.
But what if the banding comes from your random number generator?
Psychic moment!
I just yesterday switched from rand() to Mersenne Twister. No significant changes occurred, that I could tell anyway.
The following code calculates the Bekenstein-Hawking entropy of a unit sphere, using t Hooft’s holographic principle:
#include <iostream>
using namespace std;
int main(void)
{
long double c3 = pow(299792458.0, 3.0);
long double G = 6.6743e-11;
long double pi = 4.0 * atan(1.0);
long double h = 6.62607015e-34;
long double hbar = h / (2.0 * pi);
long double r = 1;
long double A = 4 * pi * r * r;
long double S_BH = (c3 * A) / (log(2.0) * 4.0 * G * hbar);
cout << S_BH << endl;
return 0;
}The output is n = 1.73502e+70. I'm running out of RAM when using n = 1e10. :(
I'd also like to mention that Ubuntu for WSL (https://ubuntu.com/desktop/wsl) uses 16-byte long doubles.
In the Windows environment long double is only 8-bytes, equal to the double type.
I would also like to mention that the bands are indicative of an attractor at work. More fractal-like behaviour.
OK, there's definitely something going on with the integers. Often, the intersection count reduces as distance increases (e.g. it's called falling off), and so the approximation has net shift upward, based on an angle.
vector_3 receiver_pos(r, 0, 0);
const MyBig epsilon = 0.1;
vector_3 receiver_pos_plus = receiver_pos;
receiver_pos_plus.x += epsilon;
const size_t collision_count = get_intersecting_line_count(receiver_pos, 1.0, D, true);
const size_t collision_count_plus = get_intersecting_line_count(receiver_pos_plus, 1.0, D, true);
vector_3 gradient;
gradient.x = (collision_count - collision_count_plus) / (epsilon);
const MyBig gradient_strength = G * pow(c, 3 - D) * gradient.length() * pow(receiver_pos.x, falloff_exponent);
cout << "D: " << D << " falloff exponent: " << falloff_exponent << " r: " << r << " " << gradient_strength << endl;
out_file << r << " " << gradient_strength << endl;
Here this image show that each band appears to have equal angle. The greater n, the smaller the angle.
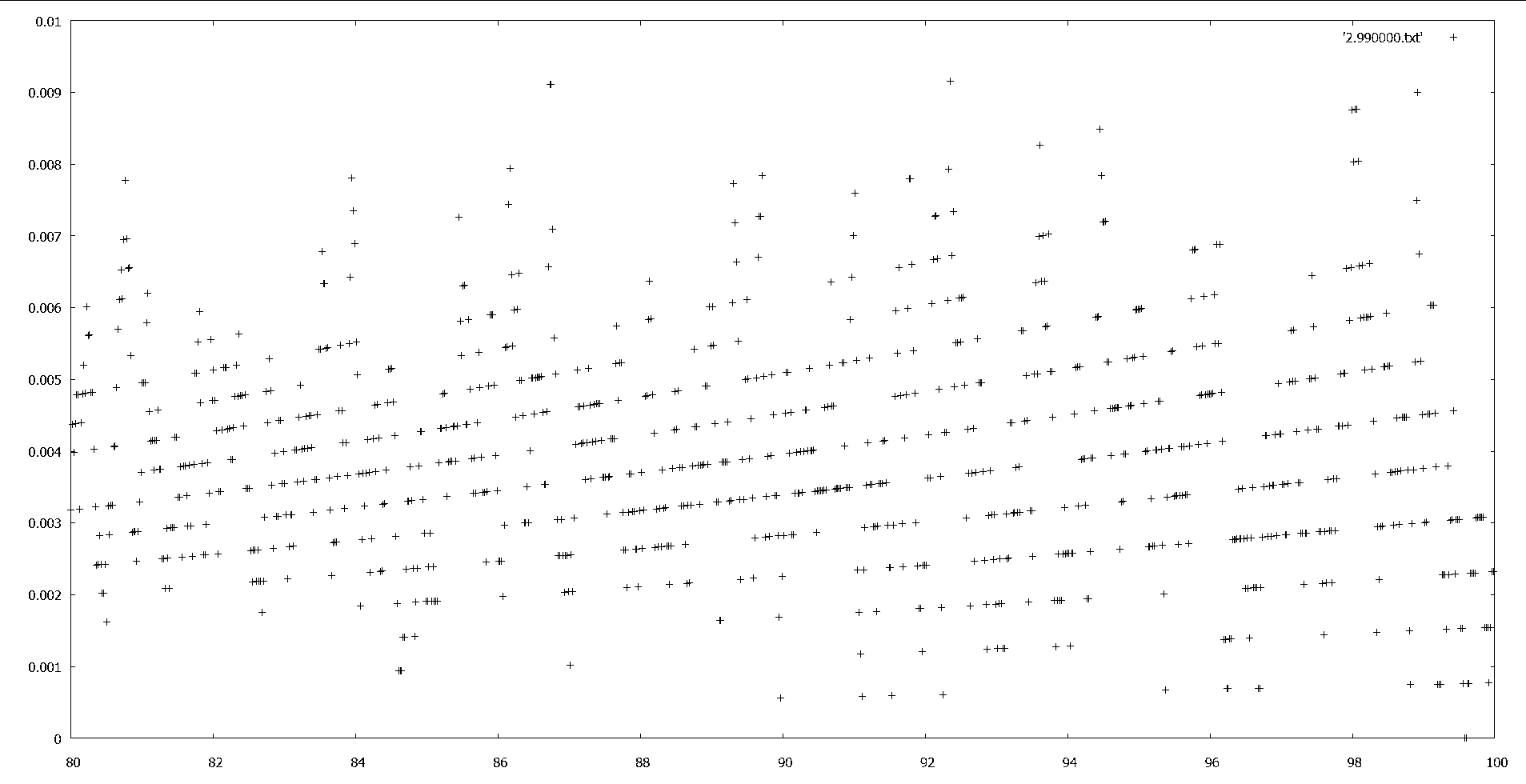
The bands are actually not straight however – they form a curve, so the band angle depends on distance as well as n.
I have a good question. Putting physics aside, how would you describe your program in terms of only geometry, or math?
I mean, there must be an explanation for the bands in those terms, ignoring incomprehensible / speculative quantum / relativistic physics stuff.
For example, i'm looking at banding too, currently:
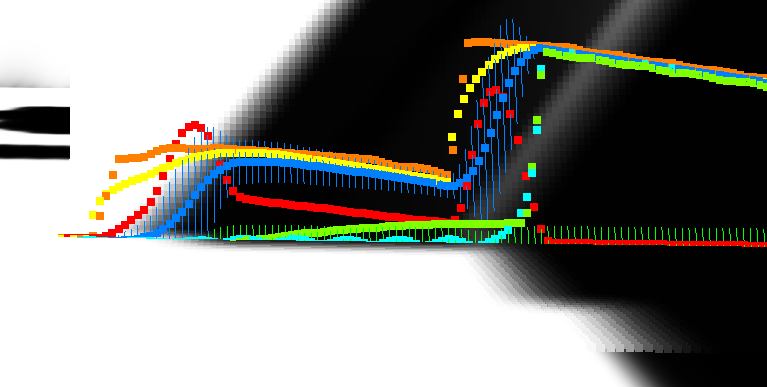
Still working on shadows, and this is a debug plot showing signals. Zooming in…
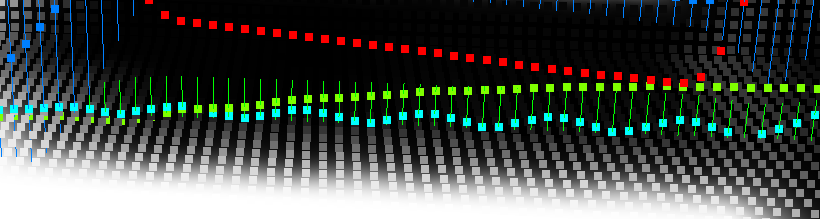
See the wave? It causes ugly ripples in my shadows, exposing the damn grid, … again! >:/
I would call this an ‘exponential smoothing’ artifact, maybe. There might be a way to get a better signal, need to figure it out…
However, it's a good example to ask another question:
Why do i think that banding needs to be fixed, but you think the banding is a mysterious, scientific discovery in your case?