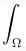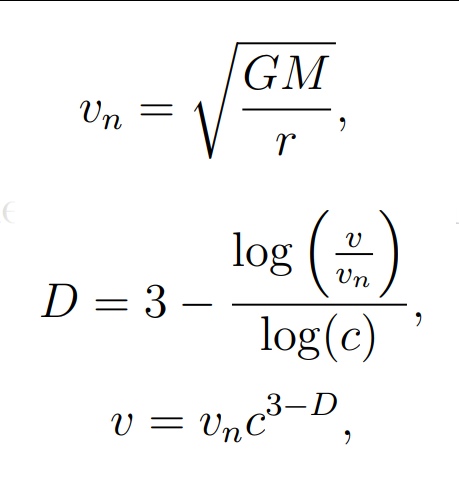JoeJ said:
But tbh, i trust the expertise of blender devs more than my ability to read the rendering eq. ; )

The problem is - you can trust them, and they likely implement their variant of rendering equation correctly, but does it match whatever you're trying to do on base level?

Let me demonstrate - these 3 rendering equations are all valid:

Where, everything is as in previous, but additionally:

• t represents specific time point
• lambda represents wavelength

All of these are correct rendering equations, but the middle one allows for temporal based effects (motion blur, etc.) and the bottom one additionally allows for spectral rendering (light dispersion for example) as it operates on wavelengths.

Does solution of the first equation for some scene become equal to the last? Only under very specific circumstances - and that's one of the major problems. Of course - f_r will often also differ, and so on (do you use only Blinn-Phong BRDF on everything, or do you even use different per different object … or even worse, different B*DF functions - some using subsurface scattering, some not … participating media also breaks this massively, etc.).

This being said - you did eliminate most of the other properties and removed different f_r (by forcing diffuse-only) - thus likely making the rendering equation the same.

In technical/academic paper it is necessary that you additionally prove (to what I mentioned that needs to be proven) that conditions are the same - otherwise the whole comparison loses sense. This becomes mathematically even more challenging than proving that your naive integrator actually works correctly for given rendering equation.

EDIT: Well… not necessarily you need to prove, but not doing so may end up in various questions. Of course doing a mistake there can make your whole work irrelevant.

You have no idea how long it took me to figure out what symbols like these actually mean.

And i can't read music notation either. I had to learn by ear. 
With math it's the same thing. I have to reinvent the wheel first, and only after that i understand the papers about the subject. Unlike music notation, i actually want to learn math. But i never found a way.

That's actually why i'm here. I assume there are many people like me, and i guess i can help them sometimes better than you could.

This does not apply to taby ofc., who has his own theory of gravity.  

Tint is working:

Also…

Thanks to everyone for their input. I really appreciate it!

JoeJ said:
You have no idea how long it took me to figure out what symbols like these actually mean.

The fun when you come to Liouville-Neumann series and symbols like that start appearing:

Adding some further conditions/definitions for function g and f, and you're supposed to propose solution.

Those exams were hard decade back … everyone thought that what we learn is absolutely useless for real world use. Well… at least in my case, I was wrong.

EDIT: Let me out of curiosity try whether GPT is actually able to work with such problems…

EDIT 2: Nope… anything beyond basic definitions seems to be completely wrong.

taby said:
Tint is working:

It's suspicious the reflection of the black environment is not black but gold.
Oh, and there is a blue reflection on gold. That's not possible. It must be still wrong.

taby said:
Also…

Ah yes - this other symbol.

I have thought the E means summing stuff up, and the f means integration. Correct me if i'm wrong, as the picture seems to mean discretization?

Feel free to reveal the truth about gravity along the way. I can read a lot between the lines from math people. (curious emoji)

Right, for a disk-shaped gravitationally bound system with near zero pressure density, the dimension of the disk decreases from 3 to less than 3 as the distance from the core increases (as the system flattens).

Here v is the observed speed, and v_n is the Newtonian speed.

A bit better:

	// Step two: this is the Fresnel reflection-refraction code
	// Start at the tips of the branches, work backwards to the root
	for(int i = current_buffer_index - 1; i >= 0; i--)
	{
		bool pure_refraction = false;
		bool pure_reflection = false;
		bool neither = false;
		bool both = false;

		if(rays[i].child_refract_id != -1 && rays[i].child_reflect_id == -1)
			pure_refraction = true;

		if(rays[i].child_refract_id == -1 && rays[i].child_reflect_id != -1)
			pure_reflection = true;

		if(rays[i].child_refract_id == -1 && rays[i].child_reflect_id == -1)
			neither = true;

		if(rays[i].child_refract_id != -1 && rays[i].child_reflect_id != -1)
			both = true;

		float accum = 0.0;

		vec3 tint_colour = vec3(1, 0.5, 0);

		if(neither)
		{
			accum = rays[i].base_color;
		}
		else if(both)
		{
			// Fake the Fresnel refraction-reflection
			const float ratio = 1.0 - dot(-normalize(rays[i].direction.xyz), rays[i].normal);

			float reflect_accum = mix(rays[i].base_color, rays[rays[i].child_reflect_id].accumulated_color, rays[i].reflection_constant);
			float refract_accum = mix(rays[i].base_color, rays[rays[i].child_refract_id].accumulated_color, 1.0 - rays[i].refraction_constant);
		
			accum = mix(refract_accum, reflect_accum, ratio);
		}
		else if(pure_refraction)
		{
			accum = mix(rays[i].base_color, rays[rays[i].child_refract_id].accumulated_color, 1.0 - rays[i].refraction_constant);	
		}
		else if(pure_reflection)
		{
			accum = mix(rays[i].base_color, rays[rays[i].child_reflect_id].accumulated_color, rays[i].reflection_constant);
		}

		const vec3 mask = hsv2rgb(vec3(hue, 1.0, 1.0));

		float t = (tint_colour.r*mask.r + tint_colour.g*mask.g + tint_colour.b*mask.b);
		
		float x = accum;
		accum = mix(accum, t, rays[i].tint_constant);
		accum = min(x, accum);

		rays[i].accumulated_color = accum;
	}

Vilem Otte said:
EDIT: Let me out of curiosity try whether GPT is actually able to work with such problems…

EDIT 2: Nope… anything beyond basic definitions seems to be completely wrong.

Wait and see… you might need to add another EDIT pretty soon.

What will happen when it can generate 3D models with quality like Midjourney?
And soon after that, AI writing better engines than we can? What then?

I have an idea evolving…
I never thought that games should strive to become art. I became bored about art, ignored it's value.
But actually i'm changing my mind.
Maybe creating true art is the only way to beat AI?

Idk. But i do not consider AI as a tool i could use to help me.
Just look at the current situation.
They have harvested the internet over a decade, to collect all art there ever was without permission.
Regulations come too late. They have already processed the data.
And now they replace human workforce with generative AI and make big money from it.
In other words: First they rob artists, then they send them home to live under the bridge.

This does not remind me an any tool i have ever used. It's a treat, a new competitor with an unfair advantage, but not a tool.

You should quit your ChatGPT subscription, and use the money for somr true art course instead. : (

JoeJ said:
You should quit your ChatGPT subscription, and use the money for somr true art course instead. : (

Speaking of this… I haven't paid for ChatGPT myself. The only thing I've considered paying for is Github Copilot - why? It tends to be useful to write some syntax things I'd write myself. Literally things like this:

The problem I see is, I don't think it is worth (or it is saving me) $100 a year, which is their subscription cost. Ideally IDE should be able to do something like this - IntelliCode does attempt to do this for C#, I don't know of any tool for C++ or such languages.

Whenever I tried to use it to create actual code - even with exact description, it fails miserably beyond anything but basic example (which you can google for within few seconds either way).

Does it improve efficiency?

Hard to say - if you use it to just finish your default constructors or similar - like I do, to an extent yes, but it really is very minor thing. If you use it as an actual code generator for blocks of code - then there is a big no. Why? Fixing long and wrong code (especially when you'd need to run it through debugger) is often a bigger hassle than writing that code correctly from the start. At that point it actually adds more work.

What it is good for is generating examples for well known libraries and apis. Although well-documented libraries and apis already have it available, so it's really again a question “How much is it really worth?”. For poorly documented libraries, surprisingly, it provides little to no value - as it had no way to obtain the examples.

JoeJ said:
They have harvested the internet over a decade, to collect all art there ever was without permission.

This is a big problem.

Now, let's say I produce a source code - with AI assisted generation - which copies 1-to-1 some part of library that is licensed under permissive license. At that point I'm breaking the license, not the AI generation tool that stole it in the first place. This is a big problem (Microsoft, though, has advantage of selecting which repositories copilot will take data from - and it could base it of off LICENSE in that project). You can't say the same about OpenAI projects.

OpenAI is well known to steal the data and use them (it's not hard to find that - because - their datasets for specific versions of ChatGPT can be found). That's a big oof and potentially a big legal problem in future. The legislation will come with a lag behind technology - but it is more than likely - that GPT authors will have to prove source of the data they learned from.

JoeJ said:
What will happen when it can generate 3D models with quality like Midjourney? And soon after that, AI writing better engines than we can? What then?

It depends on how costly it will be for that generative AI, and where it got data to learn from. So far I haven't seen the economical figures - but the amount of resources you need to build good GPT is huge, computational requirements are huge, etc.

Further, for an author/artist it is impossible to prove whether GPT used his work as source of learning data (i.e. for GPTs we can't use principle of “presumption of innocence” and the burden of proof has to be on side of GPTs - Why? - because they can just set their source data as non-published - which OpenAI did with GPT 3.0 and newer).

I know we went a bit away from the topic, my apologize to taby for that.