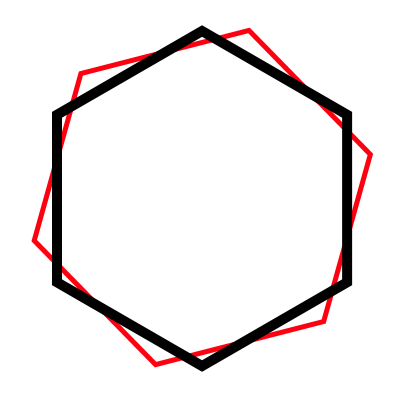
To simplify the question, I'm boiling down one of the mechanics of my game into two hexagons. The mechanic comes down to rotating the black hexagon to align with the red hexagon. The black hexagon will encounter red hexagons that are oriented around an arbitrary angle. The black hexagon will rotate smoothly to match the orientation of the next selected red hexagon. The red hexagons might not be perfect hexagons. That is, they might be slightly deformed and the angles of the corners might be bigger or smaller than 60 degrees.

The alignment portion of the rotation (getting all vertices to align with other vertices) is straightforward:

• Choose a reference vector (e.g. Vector2.UnitY)
• Determine the topmost vertex and calculate the angle between it and the reference vector
• Apply rotation with the given angle

The problem is that eventually, the orientation will have a full 60/-60 rotation in it. The reason is simple, depending on which hexagon selected next, the new “topmost” vertex might now be on the other side (e.g. shift from +x to -x).

At first, I figured that this is just a matter of selecting the topmost vertex with the smallest angle by comparing the absolutely value of the topmost and second topmost angles. But this makes no difference, eventually, the 60/-60 degree rotation will still be applied, because either side will have a new topmost vertex.

I tried a number of approaches including constraining the maximum orientation to 30 degrees (and then flipping to the other angle). But with every approach I try, at some point, I once again hit the 60 degree rotation, either in cases where the orientation reaching a flat top, or the angles are being exchanged.

Am I hitting some sort of a mathematic constraint and/or this simply not possible? Is there no way to orient one hexagon with another with an arbitrary angle without eventually doing a full 60-degree rotation?

Am I hitting some sort of a mathematic constraint and/or this simply not possible?

Such problem can be handled without any issues if you use complex numbers instead angles.
Form 6 points you can make 6 vectors form point to polygon center, then make complex numbers from vectors, raise them yo the 6th power, add them together, then you get the best fitting orientation of a regular hexagon.

I hope saying ‘raise to the 6th power’ is correct, not sure. But i can write some code if you want…

@JoeJ I would definitely appreciate an example because I've never worked with complex numbers in code.

CombatHammie said:
I've never worked with complex numbers in code.

So i decided not using them either to make it more intuitive.

I'm pretty sure this is exactly what you want. I can gradually change the shape and rotate the polygon, and the result never ‘jumps’ or something, and it looks as similar as possible.

The interesting code is in the middle. 
To get average orientation, simply divide all angles by 6, make unit vector from this new angle, multiply it by weight and accumulate.
After that take angle from resulting vector, multiply by 6 and rotate 6 times by (360/6) degrees to get the new points.

The only question is what weighting to use (pWeight).
I have used squared length, but you should also try length, or simply 1 for uniform weights.

		static bool visMakePolygonRegular = 1; ImGui::Checkbox("visMakePolygonRegular", &visMakePolygonRegular);
		if (visMakePolygonRegular)
		{
			static int numPoints = 6; ImGui::DragInt("numPoints", &numPoints, 0.1f);
			static float angularRandomness = 0.1f; ImGui::DragFloat("angularRandomness", &angularRandomness, 0.01f);
			static float linearRandomness = 0.1f; ImGui::DragFloat("linearRandomness", &linearRandomness, 0.01f);
			static float rotation = 0; ImGui::DragFloat("rotation", &rotation, 0.01f);
			static float size = 1; ImGui::DragFloat("size", &size, 0.01f);
			

			// make prcedural test polygon and calc center

			std::vector<vec2> polygon;
			for (int i=0; i<numPoints; i++)
			{
				float angle = (float(i) + PRN::randF(i)*angularRandomness) / float(numPoints) * float(PI*2) + rotation;
				float len = (1 + PRN::randF(i*3+10) * linearRandomness) * size;
				polygon.push_back( vec2(cos(angle)*len, sin(angle)*len) );
			}

			for (int i=0; i<numPoints; i++)
				RenderLine(polygon[i], polygon[(i+1)%numPoints], 0,1,0); 
			
			float degree = float(numPoints);

			vec2 center (0,0);
			for (int i=0; i<numPoints; i++)
				center += polygon[i];
			center /= degree;


			// calculate best fit orientation

			vec2 orientation(0,0);
			for (int i=0; i<numPoints; i++)
			{
				vec2 pVec = polygon[i] - center;
				//float pWeight = pVec.Length();
				float pWeight = pVec.Dot(pVec);
				float angle = atan2 (pVec[1], pVec[0]) * degree;
				orientation += vec2( pWeight*cos(angle), pWeight*sin(angle) );
			}
			
			// construct unit vectors for new points

			float theta = atan2 (orientation[1], orientation[0]) / degree;
			
			std::vector<vec2> regularPolygon (polygon.size());
			for (int i=0; i<numPoints; i++)
			{
				float phi = theta + float(i)*float(PI*2) / degree;
				regularPolygon[i] = vec2 (cos(phi), sin(phi));// + center;
			}


			// finally translate and scale to preserve area and center

			float doubleArea = 0;
			float doubleRegularArea = 0; // i'm too lazy figuring out how to calc this analytically :)
			for (int i=0; i<numPoints; i++)
			{
				int j = (i+1) % numPoints;
				doubleArea += (polygon[j][0] + polygon[i][0]) * (polygon[j][1] - polygon[i][1]); 
				doubleRegularArea += (regularPolygon[j][0] + regularPolygon[i][0]) * (regularPolygon[j][1] - regularPolygon[i][1]); 
			}
			float scale = sqrt(doubleArea / doubleRegularArea);
			for (int i=0; i<numPoints; i++)
				regularPolygon[i] = regularPolygon[i] * scale + center;

			for (int i=0; i<numPoints; i++)
				RenderLine(regularPolygon[i], regularPolygon[(i+1)%numPoints], 1,1,1); 
		}

One more uncertainty: Instead making vectors from point to center, you can also make them from point to next point:

pVec = polygon[i] - polygon[(i+1) % numPoints];

So you try to match the edges.
I've tried this and it seems better to me, also it does not require to calculate center. (Calculating a center by averaging the points is trivial but might not be the best way, it's possible to calculate a proper centroid that takes area into account).

Thinking of all this, i now conclude using edge and edge length is the best option:

vec2 orientation(0,0);
			for (int i=0; i<numPoints; i++)
			{
				//vec2 pVec = polygon[i] - center;
				vec2 pVec = polygon[i] - polygon[(i+1) % numPoints];
				float pWeight = pVec.Length();
				//float pWeight = pVec.Dot(pVec);
				float angle = atan2 (pVec[1], pVec[0]) * degree;
				orientation += vec2( pWeight*cos(angle), pWeight*sin(angle) );
			}

I have some code to calculate centroid es well, but it is very ugly : )

The reason proper centroid might be useful is this:

Imagine this polygon, with an additional vertex (X) with both edges being on the same line.
Cantroid calculation gives the same result if this vertex exists or not, while tirvial center as above gives different result.
So centroid would help with optimal position of the new polygon.
This example also makes me think length is the best weight, because we also get equal results for such a case.

inline float PolygonAreaAndCentroid2D (float *centroid, float *p, const int32_t stride, const int32_t numPoints, const int32_t Y = 1)  
{
 float area = 0;
 char *p0 = (char*) p;
 char *p1 = p0 + stride * (numPoints-1);
 centroid[0] = 0;
 centroid[Y] = 0;
 if (numPoints<=0) return 0.0f;

 float minX = FLT_MAX; // calculate bbox to resolve precision issues
 float maxX = -FLT_MAX;
 float minY = FLT_MAX;
 float maxY = -FLT_MAX;

 for (int32_t i=0; i<numPoints; i++)  
 {
  float v0x = ((float*) p0)[0] - p[0];
  float v0y = ((float*) p0)[Y] - p[Y];
  float v1x = ((float*) p1)[0] - p[0];
  float v1y = ((float*) p1)[Y] - p[Y];
  float a = v0x*v1y - v1x*v0y;
  area += a;  
  centroid[0] += (v0x + v1x)*a;
  centroid[Y] += (v0y + v1y)*a;
  minX = min(minX, v0x);
  maxX = max(maxX, v0x);
  minY = min(minY, v0y);
  maxY = max(maxY, v0y);
  p1 = p0;
  p0 += stride;
 }

 if (fabs(area) < FP_EPSILON2)
 {
  centroid[0] = p[0];
  centroid[Y] = p[Y];
  return 0;
 }  

 centroid[0] /= (3.0f * area);
 centroid[Y] /= (3.0f * area);
 if (centroid[0] > maxX || centroid[0] < minX) centroid[0] = (maxX+minX) * 0.5f;
 if (centroid[Y] > maxY || centroid[Y] < minY) centroid[Y] = (maxY+minY) * 0.5f;
 centroid[0] += p[0];
 centroid[Y] += p[Y];
 return area * 0.5f;
} 

… i got some doubts about this edge thing, and yes - when using 5gon or quad, result shows the mistake. Quad is rotated 45 degrees for example.
So it's no good idea, forget about it.

But i made the proposed change using centroid, and result is a bit better. More overlapping areas of input and output.

So this is the improvement using the ugly centroid function. But code from first post is probably good enough as well.

Centroid function is ugly because area can become tiny, and floating point issues cause things like centroid being outside of the polygon. Thus i added a bounding box check which is just a hack.
Also i wanted the function to be compatible with any vec2 / 3 / 4, which did not help with beauty either : )

static bool visMakePolygonRegular = 1; ImGui::Checkbox("visMakePolygonRegular", &visMakePolygonRegular);
		if (visMakePolygonRegular)
		{
			static int numPoints = 6; ImGui::DragInt("numPoints", &numPoints, 0.1f);
			static float angularRandomness = 1.1f; ImGui::DragFloat("angularRandomness", &angularRandomness, 0.01f);
			static float linearRandomness = 0.19f; ImGui::DragFloat("linearRandomness", &linearRandomness, 0.01f);
			static float rotation = -0.04f; ImGui::DragFloat("rotation", &rotation, 0.01f);
			static float size = 1.57f; ImGui::DragFloat("size", &size, 0.01f);
			

			// make prcedural test polygon and calc center

			std::vector<vec2> polygon;
			for (int i=0; i<numPoints; i++)
			{
				float angle = (float(i) + PRN::randF(i)*angularRandomness) / float(numPoints) * float(PI*2) + rotation;
				float len = (1 + PRN::randF(i*3+10) * linearRandomness) * size;
				polygon.push_back( vec2(cos(angle)*len, sin(angle)*len) );
			}

			for (int i=0; i<numPoints; i++)
				RenderLine(polygon[i], polygon[(i+1)%numPoints], 0,1,0); 
			
			float degree = float(numPoints);


			vec2 center (0,0);
			float area = PolygonTools::PolygonAreaAndCentroid2D ((float*)&center, (float*)polygon.data(), sizeof(vec2), numPoints);


			// calculate best fit orientation

			vec2 orientation(0,0);
			for (int i=0; i<numPoints; i++)
			{
				vec2 pVec = polygon[i] - center;
				float pWeight = pVec.Length();
				float angle = atan2 (pVec[1], pVec[0]) * degree;
				orientation += vec2( pWeight*cos(angle), pWeight*sin(angle) );
			}
			
			// construct unit vectors for new points

			float theta = atan2 (orientation[1], orientation[0]) / degree;
			
			std::vector<vec2> regularPolygon (polygon.size());
			for (int i=0; i<numPoints; i++)
			{
				float phi = theta + float(i)*float(PI*2) / degree;
				regularPolygon[i] = vec2 (cos(phi), sin(phi));// + center;
			}


			// finally translate and scale to preserve area and center

			float doubleRegularArea = 0; // i'm too lazy figuring out how to calc this analytically :)
			for (int i=0; i<numPoints; i++)
			{
				int j = (i+1) % numPoints;
				doubleRegularArea += (regularPolygon[j][0] + regularPolygon[i][0]) * (regularPolygon[j][1] - regularPolygon[i][1]); 
			}
			float scale = sqrt(fabs(area)*2 / fabs(doubleRegularArea));
			for (int i=0; i<numPoints; i++)
				regularPolygon[i] = regularPolygon[i] * scale + center;

			for (int i=0; i<numPoints; i++)
				RenderLine(regularPolygon[i], regularPolygon[(i+1)%numPoints], 1,1,1); 
		} 

I don't have the words to describe how grateful I am to you, @joej!

Regardless of which approach is taken (thanks for showing both ideas), the solution is ultimately in what you did in either of the two code blocks below.

My problem was that no matter which approach I took, I was stuck thinking that the rotation must be done against a fixed reference vector. I had to re-read your code a few times to finally understand how a weighted average works here without creating an arbitrary rotation.

Your code works perfectly in my engine and I no longer have any 60/-60 rotations in any of the previous cases!

vec2 orientation(0,0);
			for (int i=0; i<numPoints; i++)
			{
				//vec2 pVec = polygon[i] - center;
				vec2 pVec = polygon[i] - polygon[(i+1) % numPoints];
				float pWeight = pVec.Length();
				//float pWeight = pVec.Dot(pVec);
				float angle = atan2 (pVec[1], pVec[0]) * degree;
				orientation += vec2( pWeight*cos(angle), pWeight*sin(angle) );
			}

			// calculate best fit orientation

			vec2 orientation(0,0);
			for (int i=0; i<numPoints; i++)
			{
				vec2 pVec = polygon[i] - center;
				//float pWeight = pVec.Length();
				float pWeight = pVec.Dot(pVec);
				float angle = atan2 (pVec[1], pVec[0]) * degree;
				orientation += vec2( pWeight*cos(angle), pWeight*sin(angle) );
			}

CombatHammie said:
the solution is ultimately in what you did in either of the two code blocks below.

The one on top (using edges) is surely wrong - it only works because with hexagon the error cancels out, but if is not regular, error creeps in but is not very noticable.

CombatHammie said:
I had to re-read your code a few times to finally understand how a weighted average works here without creating an arbitrary rotation.

The weighting is not so important for understanding, but the multiplication and division by degree.

The way i figured this out was this:

Task was to calculate curvature directions on a mesh. To get this, one could take the adjacent edge directions times the angle between triangles on each edge.
But this generates vectors in all directions, and two directions being the exact opposite of each other are in the same line, so how could i add them together without making them cancel each other out?

So, like you i tried to take angles to a fixed direction, e.g. the first edge of the vertex.
But it does not work to force all angles to be on the same 180 degree range, just like it does not work to flip directions so they all point to the same half space. The resulting average is wrong and depends on the choice of reference direction.

So i asked how to get a proper average from multiple angles, and i've learned it's as simple as making unit direction vectors form that angle, take average from those vectors and take angle from that.
But this still does not solve the problem of opposite directions should give us the same value. (Or 6 directions in 30 degrees steps like in your case)
Now, if we multiply the angles by 2, opposite vectors do give the same result. So we do this for the averaging process, and divide by 2 again to get our average. And it worked and did not depend on the orientation of reference direction to measure angles.

Later i have used this to calculate line-, cross- or hex-fields on meshes successfully, and only after that i understood what math guys mean when they talked about using complex numbers to represent their fields in their papers. :D

JoeJ said:

CombatHammie said:
the solution is ultimately in what you did in either of the two code blocks below.

The one on top (using edges) is surely wrong - it only works because with hexagon the error cancels out, but if is not regular, error creeps in but is not very noticable.

CombatHammie said:
I had to re-read your code a few times to finally understand how a weighted average works here without creating an arbitrary rotation.

The weighting is not so important for understanding, but the multiplication and division by degree.

The way i figured this out was this:

Task was to calculate curvature directions on a mesh. To get this, one could take the adjacent edge directions times the angle between triangles on each edge.
But this generates vectors in all directions, and two directions being the exact opposite of each other are in the same line, so how could i add them together without making them cancel each other out?

So, like you i tried to take angles to a fixed direction, e.g. the first edge of the vertex.
But it does not work to force all angles to be on the same 180 degree range, just like it does not work to flip directions so they all point to the same half space. The resulting average is wrong and depends on the choice of reference direction.

So i asked how to get a proper average from multiple angles, and i've learned it's as simple as making unit direction vectors form that angle, take average from those vectors and take angle from that.
But this still does not solve the problem of opposite directions should give us the same value. (Or 6 directions in 30 degrees steps like in your case)
Now, if we multiply the angles by 2, opposite vectors do give the same result. So we do this for the averaging process, and divide by 2 again to get our average. And it worked and did not depend on the orientation of reference direction to measure angles.

Later i have used this to calculate line-, cross- or hex-fields on meshes successfully, and only after that i understood what math guys mean when they talked about using complex numbers to represent their fields in their papers. :D

We're on the same page in terms of understanding this, but allow me to clarify the specific implementation I used. The edge (top) vs vertex (bottom) semantic wasn't important. The part that was “broken” in my attempts was me thinking that I must use a fixed reference (control). In both of your code blocks, you're not doing that. Whereas in my approach, I was relying on a fixed, predefined vector as the point of reference to where the “alignment” vector should be.

My actual implementation (adapted to the specifics of the mechanic used in the game) is taking what you have in the second block and then anchoring that to a reference “driver” vertex (unrelated to the post and your code) that defines the actual control in the game. I've put hundreds of random hexagon through a reference hexagon since your reply, and haven't seen a single “flip”. It surely works as intended. ?

CombatHammie said:
We're on the same page in terms of understanding this, but allow me to clarify the specific implementation I used. The edge (top) vs vertex (bottom) semantic wasn't important. The part that was “broken” in my attempts was me thinking that I must use a fixed reference (control). In both of your code blocks, you're not doing that. Whereas in my approach, I was relying on a fixed, predefined vector as the point of reference to where the “alignment” vector should be. My actual implementation (adapted to the specifics of the mechanic used in the game) is taking what you have in the second block and then anchoring that to a reference “driver” vertex (unrelated to the post and your code) that defines the actual control in the game. I've put hundreds of random hexagon through a reference hexagon since your reply, and haven't seen a single “flip”. It surely works as intended. ?

It's worth to note that both reference and flips are still there, just ‘hidden’.
For you, the reference is the global coordinate system (used to take angles), and flips are always exact 30 degrees so not visible (but maybe need to be handled, e.g. if you would use the hex to orient a character).

It's visible for my cross fields, which i use to guide curvature aligned remeshing:

So i use a degree of 4 because i want regular quads. Degree of 6 (like you do) is used for remeshing that aims to generate equiangular triangles, btw.

So in above image i visualize a cross at each vertex, and the very first direction is shown in white. For reference i simply use an arbitary tangent made from vertex normal and global coordinate system.
And you see the first direction seems consistent mostly, but in the corner there is a flip of 90 degrees. 

So this can not be prevented but it never makes any problem that can't be solved. 
For example, to trace a curved streamline on the surface that is aligned to the field, we need to select the next direction to be the one most similar to the current. A walking character in a game would have to address this same problem.