2D physics libraries like Box2D and Chipmunk are fine things, but not for every game. Sometimes they're total overkill. Other times, technical constraints force you to go your own way. Sometimes you just want to avoid the well-worn path trod by countless Limbo and Angry Birds knock-offs. Whatever the reason, here are some algorithms to get you started should you opt to do it yourself. BACKGROUND Having worked on a physics-library-based space shooter, I was acutely aware of the difficulties. First of all, you need concave polygons. Our spaceships weren't, so we had to divide them into a bunch of little triangles using a fancy algorithm. When the ships collided, the triangles would fly apart and snap back together as if held together with elastic, sometimes with part of the other ship wedged in between - not the effect we had in mind. And then there were issues with "bullet tunneling", and the general pain of storing part of our objects' state in a black box - even if it is an open-source black box. If I had to do it all over again, I'd use simple bounding-circle collisions. That's exactly what the MARS guys did. After that ordeal, and with HTML5 coming into vogue a few years back, I decided to make a nice, simple, slow-paced, sailing ship battle game... in JavaScript. I tried a JS port of the Chipmunk physics engine, but it was just too slow. So, I looked up the algorithms I really needed, and implemented them in about 100 lines of JavaScript. And when HTML5 soured on me and I switched to C++ for my next game, porting the code was a piece of cake. I love working this way. DESIGN There are three kinds of objects in my naval combat game: 1. Ships - a few slow-moving convex polygons 2. Cannonballs - many fast-moving point particles 3. Land masses - a few large static polygons I only need to check for ship-vs-ship, ship-vs-cannonball, and ship-vs-land collisions. What are the algorithms for those? 1. Ship vs Cannonball - polygon vs line segment. 2. Ship vs Land - point vs polygon. Shorelines are fuzzy and imprecise, so for this purpose I treat ships as point particles. 3. Ship vs Ship - polygon vs polygon, specifically convex hulls (literally!) There's no need for joints, polygon stacking, or polygon-vs-polygon continuous collision detection (Box2D creator Erin Catto wrote some great papers about that; it's rather advanced for DIYers but definitely worth reading). I also use bounding boxes for first-pass collision detection. That's just an optimization, and it's easy, so I'll leave it as an exercise to the reader. Potentially I might need a spatial partitioning scheme (e.g. quadtrees) if I create an MMO with huge sprawling maps. I haven't done that, and it could get complicated, so I'll leave it at that and move on. ALGORITHMS A few notes on the following code: - This is working JavaScript code from my game, with only minor edits for clarity. - Porting to C, C++, and similar languages should be very direct in most cases. - Polygons are stored as flat interleaved arrays: [x1,y1, x2,y2, ...] - Points are stored as [x,y] arrays for consistency with polygons. (Yes, p[0] is a little harder to type than p.x but I got used to it and I prefer it now. And anyway, it'll be a moot point if/when array-oriented languages come back into vogue.) One piece of advice: if you intend to roll your own physics engine, allow yourself a few weeks to iron it out (maybe months, if you have ambitious goals). Study the algorithms. Code up some demos. Step through the algorithms in a debugger. Get comfortable with the math. Look for other algorithms that might suit your particular needs better than these ones. LINE VS LINE This is the standard line intersection formula, useful for all kinds of things. function lineIntersection(a,b, c,d){ var v,u,d,r,s; v= [ d[0]-c[0], d[1]-c[1] ]; u= [ b[0]-a[0], b[1]-a[1] ]; d= u[0]*v[1] - u[1]*v[0]; r= ((a[1]-c[1])*v[0] - (a[0]-c[0])*v[1]) / d; s= ((a[1]-c[1])*u[0] - (a[0]-c[0])*u[1]) / d; return (0<=r && r<=1 && 0<=s && s<=1); } LINE VS POLYGON To detect when a cannonball hits a ship, trace a line from the cannonball's previous position (last frame) to its current position, and test to see if it crossed any line segment of the ship's hull. This is reasonably accurate even if the framerate drops to a miserable 10 fps. This is an easy form of Continuous Collision Detection that's ideal for CCD's main use cases: bullets and beam weapons. // a, b = [x,y] // edges = [x1,y1, x2,y2, ...] // function linePolygonIntersection(a,b, edges){ var c,d,i; d= edges.slice(edges.length-2); for(i=0; i POINT VS POLYGON 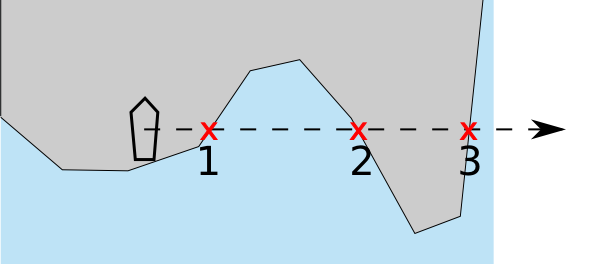This is one of the many elegant "even-odd rule" algorithms. Starting at the point in question, trace a line in any direction and count how many times it crosses the polygon. If it's an odd number, the point is inside the polygon. It's really just a Line-vs-Polygon algorithm, optimized for a horizontal line. // point = [x,y] // polygon = [x1,y1, x2,y2, ...] // function isPointInPolygon(point, polygon){ var tx= point[0], ty=point[1]; var a; var b= polygon.slice(polygon.length-2); var yflag0= (b[1] >= ty); var yflag1; var inside_flag=false; for(var j=0; j= ty); if(yflag0 != yflag1){ // vertexes straddle our point's Y-coord: potential hit. // LERP to check X-coord... if(yflag1 == ((b[1]-ty) * (a[0]-b[0]) >= (b[0]-tx) * (a[1]-b[1]))) inside_flag= !inside_flag; } yflag0= yflag1; } return inside_flag; } POLYGON VS POLYGON I'm using the Separating Axis Theorem (SAT) algorithm. It's not "the best" but it's relatively simple and fast enough for most purposes. 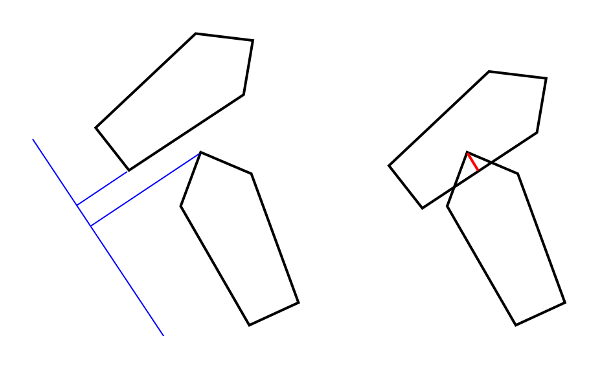Right: if we project along every line of both ship polygons, we always get an overlap (no separation), so the ships have collided. The axis with the smallest overlap (red) provides the 'separation vector' which tells us exactly how far we must move one ship to resolve the collision state. We could also move each ship half that amount, or whatever makes sense. Left: there is at least one separating axis, therefore the ships have not collided. // Algorithm: // For each side, compute its "axis" (normal vector), B. Normalize it. // Project each vertex, of both polygons, onto the axis. // Note: dot(A,B) is an adequate approximation of proj(A,B) for this purpose. // Keep track of min and max values for each polygon. // If there's an axis with no overlap - a SEPARATING AXIS - we can stop. // If the min/max values overlap on all sides, we have a collision. // Use the smallest overlap to separate the shapes. // // P1,P2 = two *convex* polygons in [x,y, x,y, ...] format // cx = canvas context for debug drawing (optional) // function collidePolyPoly(P1, P2, cx){ var collision= true; var dmin= -Infinity; var collaxis= null; function _projectVerts(P1, P2, flip){ var A=P1, B=P2; var v1; var v2= A.slice(A.length-2); for(var i=0; imaxA) maxA=t; } var minB= vdot(axis, B.slice(0,2)); var maxB= minB; for(var j=2; jmaxB) maxB=t; } var d0= minA-maxB; var d1= minB-maxA; var d= Math.max(d0,d1); if(d>0){ collision=false; return null; } if(d>dmin){ // keep track of minimum separation vector dmin=d; collaxis={ vector: axis, dist: d, midpt: midpt, poly: (d0d1)^flip, }; } } } _projectVerts(P1,P2,false); if(!collision) return null; _projectVerts(P2,P1,true); if(!collision) return null; var sep= vscale(collaxis.vector, collaxis.dist); if(cx) drawLine(cx, collaxis.midpt, vadd(collaxis.midpt, sep), 'red', 0.2); return { vector: sep, poly: collaxis.poly, flip: collaxis.flip, }; } // vector math helpers function vadd(a,b){ return [a[0]+b[0], a[1]+b[1]]; } function vsub(a,b){ return [a[0]-b[0], a[1]-b[1]]; } function vscale(v,s){ return [v[0]*s, v[1]*s]; } function vdot(a,b) { return a[0] * b[0] + a[1] * b[1]; } function vcross(a,b) { return a[0] * b[1] - a[1] * b[0]; } function vlerp(a, b, lerp) { return [a[0] + lerp * (b[0] - a[0]), a[1] + lerp * (b[1] - a[1])]; } function vnormal(v){ // return a perpendicular unit vector var mag = Math.sqrt(v[0]*v[0] + v[1]*v[1]); return [-v[1]/mag, v[0]/mag]; // normalize & perpendicularize } // debug-draw helper function drawLine(cx, p1, p2, color, weight){ if(!cx) return; cx.strokeStyle=color; cx.lineWidth=weight; cx.beginPath(); cx.moveTo(p1[0],p1[1]); cx.lineTo(p2[0],p2[1]); cx.stroke(); } NOTES I mentioned that I'm using similar algorithms in my current C++ sidescroller project. One advantage over physics libraries is that I'm able to use the same structure-of-arrays data for collisions, skeleton animation, and rendering. These old algorithms are heavy on Structures-of-Arrays, a staple of modern CPU/GPU/cache optimization and Data Oriented Design. That was a happy accident. The code felt questionable to me at first, I hadn't heard of DOD, and optimization would have been premature at the time. It was only when I started porting to C++/OpenGL that I realized how well these algorithms fit today's hardware. While backporting recent improvements from C++ to JS, I used interleaved arrays to overcome JS's lack of pointers. For example, by storing splines as flat arrays (ax1,ay1, ax2,ay2, ax3,ay3, ...) I can refer to any spline node, point, or x/y value by an array index, which eliminates a bit of slow/cumbersome indirection. SOURCES Line Intersection formula from the comp.graphics.algorithms FAQ (section 1.03) Point vs Polygon ptinpoly.c (by Eric Haines, in Graphic Gems IV) (I used the last algorithm, "CrossingsMultiplyTest") SAT visual explanation + Flash demo SAT tutorial with formulas + VB code Related article on gamedev.net: Shooting At Stuff (how to aim at moving targets) ARTICLE UPDATE LOG 29 Nov 2015: Initial release 2 Dec 2015: Formatting fixes