In the age of graphics accelerator cards, I find it hard to believe that anyone would need such an algorithm. I had enough interest at one time to develop this into a class (although I don't know if I'll ever use it). Maybe the idea may be useful, maybe all of the gurus already have thought of it (and found it really quite useless). Whatever the case, I'd like to present this entertaining algorithm because it's the last one I came up with before I considered software acceleration a lost cause.
[size="5"]Ideas Behind the Method
The main reason why someone would like to avoid redrawing over pixels is the slow access time for memory compared to the speed at which microprocessors run. Faster memories or large caches could help eliminate this problem, but let's assume we don't have either. What we need is a way to access memory as little as possible, and that's what I propose. (Writing to memory can take longer than reading from memory, so replacing writes to memory with reads from memory can also help increase the speed of drawing.)
I also considered the move of graphics from low resolutions to high resolutions. This could mean larger images are trying to be displayed with relatively small holes or transparent regions. Most of the image would have pixels to be drawn. An algorithm that simply drew over previously drawn pixels would have a large amount of cycles used on a redraw. This would mean a method with little or no overwriting of pixels designed so that few, yet detailed, holes could be allowed in displayed images would be beneficial.
One possible method would be to use a z-buffer. Sort the images so that they are drawn from closest to furthest. This would reduce the number of redrawn pixels in the image and z-buffer. Of course, a read per pixel would be required in the z-buffer. Every pixel drawn also requires a write to the z-buffer, so this causes a penalty of an extra write per pixel. If there is an incredible amount of overlap, this might pay off in the end, but I didn't want this two writes per pixel penalty.
My method would still require the images to be sorted and drawn from closest to furthest. A special buffer of memory would then be used to determine whether a pixel had been already drawn in a location or not. Initially this seems like the z-buffer approach, except that we actually loose the chance to have images with depth. Looking closer however, we can design this buffer so that it reduces the number of writes and reads to memory. All we need is an intuitive interface and then build something to handle the way the buffer is used. All it needs to do is determine whether pixels are present or not. If it can do this efficiently, more time can be spent drawing to memory than anything else.
[size="5"]Mass Skip and Draw
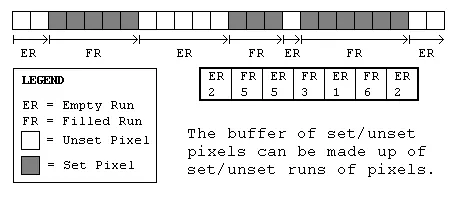
One way to organize the data to increase the efficiency of drawing would be to make the buffer contain information about horizontal lines of pixels (henceforth known as a run). Instead of saying if a particular pixel is set or not, it can say whether or not a whole row of pixels are set. Assuming our graphics are drawn using runs, large numbers of pixels can be skipped (not even checked) if we can determine that they will not be drawn. Similarly, large numbers of pixels can be drawn without further checking.
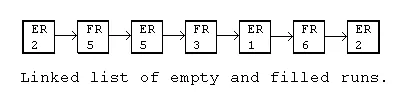
An important consideration once we have decided to represent the buffer as a row of set/unset runs would be the data structure to store them in. Since we will undoubtedly be modifying the size of the runs and perhaps adding new set runs in the middle of unset runs, it needs to be a structure which facilitates adding new runs in between old ones. A linked list type structure would appear to be the best structure in this case.
When checking to see if a run of pixels is either set or unset, we must start from the front of the list and search for the correct position in the list. Once we have located the starting location we can tell how many pixels in a row are either set or unset. Now we have another problem! If we have hundreds of thousands of pixels, we may have hundreds of unset runs! This wouldn't be good because drawing graphics found at the end of the list might take awhile! We must find a way to either shorten the list or add a random access element to our buffer... or both.
[size="5"]Divide and Conquer
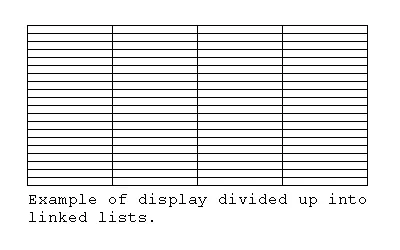
If the buffer was made of multiple linked lists, we could reduce the problems involved in traversing them. The linked lists would be divided equally across the entire display. This way each linked list could be accessed given a pixel location. Since the linked lists would be reached via array addressing, it would be a random access process (not as slow as moving through a huge linked list).
There would still be some linked list traversal, but instead of actually moving through hundreds of thousands of pixels, we'd only move through a specified number of pixels. Maybe a thousand. Maybe a hundred or so. The memory allocated for the links in the list should be static instead of dynamic (each link should not be freed and deleted separately). For this reason I suggest allocating a memory block proportional to the size of the graphics display. This should hold enough memory for the needed links.
[size="5"]Linked List Design
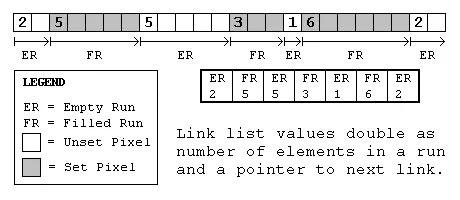
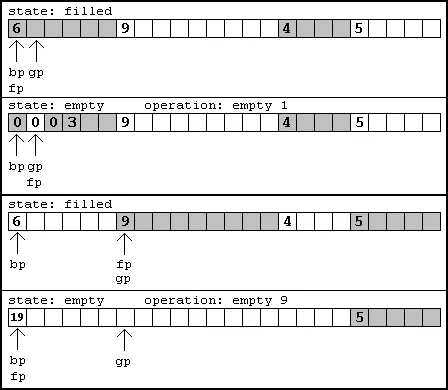
Since we allocate an amount of memory proportional to the number of pixels in the display, the simplest type of linked list structure to use would be one where the data doubled as a pointer to the next link. The data would be a number describing the number of following set or unset pixels. At the same time this value could be added to the pointer to the current link and advance it to the next link. The way this would work is by switching from filled to empty runs. If the current one was filled the next should be empty and visa versa.
Now we simply need to determine what the first run is: filled or empty. There are two ways of dealing with this problem. One method requires using the fact that none of the runs can be of zero length. The other sets aside the most significant bit as a flag to let us know whether the run is filled or empty.
If the first value is zero, it means that this one pixel isn't in the default state (the default probably being unset, so it would be set). The following pixels would then be treated as though they are filled (set). Now there is the possibility that an unset pixel follows this single set pixel, in which case another zero could indicate that it isn't set. This alternating case could go on for awhile, but once it's broken, it shouldn't occure anymore in the list. This isolates this special case to the beginning of the list.
If the most significant bit is used as a flag so that we know what the first run is, we can know what type of run follows because it will always be the alternate (and can subsequently ignore the flag bit). The problem with using the significant bit as a flag is the need to check the most significant bit with a mask and then remove it. These are two operations which could use up precious cycles when we could possibly have been simply checking for a zero.
[size="5"]Putting it All Together
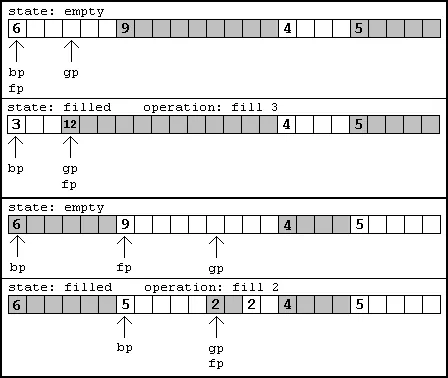
Now we know how to traverse each list and find each list. There's just one problem. The lists are not doubly linked lists, so we need to keep track of the previous link so we can modify a previous link if necessary. This means we need at least two pointers at all times while traversing a list, and a way to tell which type of run we are on (empty or filled). In my implementation I had an additional pointer called the goal pointer. Its function is to point at the start of any draw (or erase?) operation. Depending on the type of run it is in, you know whether pixels should be drawn here or you should skip ahead and draw pixels elsewhere. If you fill from the goal pointer you know how to manipulate the pointers in the linked list to represent the newly filled area. This could be simply changing current pointers in the linked list, or adding new links. Don't forget to combine any neighboring filled or empty areas caused by this operation! If you don't, you'll get a performance hit due to fragmentation!
[size="5"]Completed Design
The finished product merely consists of functions that give you information about the runs available. For example, when drawing a graphic, you'll want to know where an empty run is so you can draw something there. This is an opportunity to define the function: findEmpty. This would take an offset (place to start searching) and a range to search within. It would then return the place on the screen where something could be drawn and the number of pixels that could be drawn at that position. Other functions would be necessary for filling the buffer, like fillEmpty and emptyFill. All of these should be fairly straightforward to implement given the information above.
[size="5"]My Source Code
I attempted to implement this with some success. However I haven't tested my code comprehensively. This is due to the fact that I'm now more interested in accelerated graphics cards, and I think I may have made my class more complex than necessary. I chose to use the most significant bit flag to determine the type of run at the beginning of a linked list, although I think I would have preferred to use a zero instead. I also have a confusing method of using three pointers, where I think the code could work just as well with two pointers and something to indicate the type of run the goal pointer is on, as I discussed above.
With these many downfalls, I believe the code is as clearly commented as possible. I also tested and debugged it with some simple cases, so I know it's not as buggy as when I first typed it. Send any bug reports to me, and let me know if you use my code in any of your own programs.
- A header with types: newtypes.h
- The header file: skipgrid.h
- The C++ code: skipgrid.cpp