In the previous iteration of our game, we decided to use an actual cone as a way to make an AI "see".

This implementation was hazardous, and it quickly became one of the hardest things to implement.

We eventually were able to code it all, but the results were really static and not really realistic.

Because of the reboot, I took the time to actually identify what constraint one's vision has.

The visual field

First of all, a cone isn't really the best in therm of collision checking. It required a special collider and could have potentially been a bottleneck in the future when multiple AI would roam the level.

In actuality, the visual field can be represented as a 3D piece of a sphere (or more like a sector of a sphere).

So we're gonna need to use a sphere in the new version. It's cleaner and more efficient that way.

Here's how I've done it:

foreach (Collider otherCollider in Physics.OverlapSphere(m_head.transform.position, m_visionDistance / 2, ~LayerMask.GetMask("Entity", "Ignore Raycast"), QueryTriggerInteraction.Ignore))
{
	// Do your things here
}

Pretty simple, really...

Afterwards (not unlike our previous endeavour), we can just do a simple ray cast to see if the AI's vision is obstructed:

// Do a raycast
RaycastHit hit;
if (Physics.Raycast(m_head.position, (otherPosition - m_head.position).normalized, out hit, m_visionDistance, ~LayerMask.GetMask("Entity", "Ignore Raycast"), QueryTriggerInteraction.Ignore) && hit.collider == otherCollider)
{
	// We can see the other without any obstacles
}

But with that came another problem: if we use a sphere as a visual field, then the AI can surely see behind his back.

Enters the cross product.

Vectorial cross product

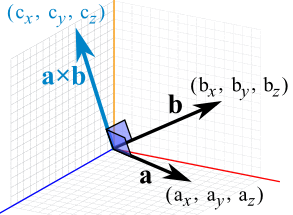
The cross product is a vectorial operation that is quite useful. Here's the actual operation that takes place:

\(\mathbf{c} = \mathbf{a} \times \mathbf{b} = ( \mathbf{a}_{y}\mathbf{b}_{z} -\mathbf{a}_{z}\mathbf{b}_{y}, \mathbf{a}_{z}\mathbf{b}_{x} -\mathbf{a}_{x}\mathbf{b}_{z}, \mathbf{a}_{x}\mathbf{b}_{y} -\mathbf{a}_{y}\mathbf{b}_{x} )\)

This actually makes a third vector. This third vector is said to be "orthogonal" to the two others.

This is a visual representation of that vector:

As you can see, this is pretty cool. It looks like the translation gizmo of many 3D editors.

But this operation is more useful than creating 3D gizmos. It can actually help us in our objective.

Interesting Properties

One of the most interesting properties of the cross product is actually its magnitude.

Depending on the angle between our two a and b vectors, the magnitude of the resulting vector changes. Here's a nice visualization of it:

As you can see, this property can be useful for many things... Including determining the position of a third vector compared to two other vectors.

But, however, there's a catch: the order of our a and b vector matters. We need to make sure that we don't make a mistake, as this can easily induce many bugs in our code.

The funnel algorithm

In one of my articles, I've actually explained how pathfinding kinda works. I've said that the navigational mesh algorithm is actually an amalgamation of different algorithms. 

One of these algorithms is the Funnel algorithm, with which we actually do the string pulling.

When the Funnel algorithm is launched, we basically do a variation of the cross product operation in order to find if a certain point lay inside a given triangle described by a left and right apexes.

This is particularly useful, as we can actually apply a nice string pulling on the identified path.

Here's the actual code:

public static float FunnelCross2D(Vector3 tip, Vector3 vertexA, Vector3 vertexB)
{
	return (vertexB.x - tip.x) * (vertexA.z - tip.z) - (vertexA.x - tip.x) * (vertexB.z - tip.z);
}

With this function, we get a float. The float in question (or more particularly its sign) can indicate whether the tip is to the left or to the right of the line described by vertexA and vertexB. (As long as the order of those vectors are counterclockwise, otherwise, the sign is inverted)

Application

Now, with that FunelCross2D function, we can actually attack our problem head-on.

With the function, we can essentially tell whether or not a given point is behind or in front of an AI.

Here's how I've managed to do it:

if ( FunnelCross2D((otherTransform.position - m_head.position).normalized, m_head.right, -m_head.right) > 0 )
{
	// otherTransform is in front of us
}

Because this is Unity, we have access to directional vectors for each Transform objects.

This is useful because we can then plug these vectors into our FunnelCross2D function and voilà: we now have a way to tell if another entity is behind or in front of our AI.

But wait, there's more!

Limit the visual angle

Most people are aware that our visual field has a limited viewing angle.

It happens that, for humans, the viewing angle is about 114°.

The problem is that, right now, our AI viewing angle is actually 180°. Not really realistic if you ask me.

Thankfully, we have our trusty FunnelCross2D function to help with that.

Let's take another look at the nice cross product animation from before:

If you noticed, the magnitude is actually cyclic in its property: when the angle between a and b is 90°, then the magnitude of the resulting vector of the cross product is literally 1. The closet the angle gets to 180° or 0°, the closest our magnitude get to 0.

This means that for a given magnitude (except for 1), there are actually 2 possible a and b vector configurations.

So, we can then try to find the actual magnitude of the cross given a certain angle.

Afterwards, we can store the result in memory.

m_visionCrossLimit = FunnelCross2D(new Vector3(Mathf.Cos((Mathf.PI / 2) - (m_visionAngle / 2)), 0, Mathf.Sin((Mathf.PI / 2) - (m_visionAngle / 2))).normalized, m_head.right, -m_head.right);

Now we can just go back to our if and change some things:

if ( FunnelCross2D((otherTransform.position - m_head.position).normalized, m_head.right, -m_head.right) > m_visionCrossLimit )
{
	// otherTransform is in our visual field
}

Then we did it! the AI only reacts to enemies in their visual field.

Conclusion

In conclusion, you can see how I've managed to simulate a 3D visual field using the trustworthy cross product.

But the fun doesn't end there! We can apply this to many different situations.

For example, I've implemented the same thing but in order to limit neck rotations.

it's just like previously, but with another variable and some other fancy codes and what not...

The cross product is indeed a valuable tool in the game developer's toolset. No doubt about it.