If you have just 5 points, it's not enough to fit the 6 coefficients of the ellipse and the results will be meaningless. It can't be unambiguosly solved without knowledge of the orbital system the ellipse is modeling. It would be like trying to determine the equation of a line given only 1 point, there are an infinite number of solutions, you need at least 2 points to determine the line mx+b since it has 2 parameters.

I think that you’re wrong about the number of degrees of freedom required for a general ellipse — https://x.com/iquilezles/status/1876019871529709874?s=46&t=46k8Lh9mHanAfxnNXbDw9Q

You seem to misunderstand, and it’s no longer my fault. The code doesn’t spit out gibberish. If the code was faulty, then it wouldn’t work 99% of the time.

In order to suspend your disbelief, here is the code:

EllipseParameters extractEllipseParameters(const Eigen::VectorXd& coefficients)
{
	double a = coefficients(0);
	double b = coefficients(1);
	double c = coefficients(2);
	double d = coefficients(3);
	double e = coefficients(4);
	double f = 1;// coefficients(5);

	// Calculate center
	double centerX = (2 * c * d - b * e) / (b * b - 4 * a * c);
	double centerY = (2 * a * e - b * d) / (b * b - 4 * a * c);

	// Calculate rotation angle
	double theta = 0.5 * atan2(b, (a - c));

	// Calculate semi-axes
	double ct = cos(theta);
	double st = sin(theta);
	double ct2 = ct * ct;
	double st2 = st * st;
	double a2 = a * ct2 + b * ct * st + c * st2;
	double c2 = a * st2 - b * ct * st + c * ct2;

	// Calculate constants
	double term = 2 * (a * centerX * centerX + b * centerX * centerY +
		c * centerY * centerY + d * centerX + e * centerY + f);

	double semiMajor = sqrt(abs(term / (2 * std::min(a2, c2))));
	double semiMinor = sqrt(abs(term / (2 * std::max(a2, c2))));

	if (a2 > c2) {
		std::swap(semiMajor, semiMinor);
		theta += pi / 2;
	}

	EllipseParameters params;
	params.centerX = centerX;
	params.centerY = centerY;
	params.semiMajor = semiMajor;
	params.semiMinor = semiMinor;
	params.angle = theta;

	return params;
}

EllipseParameters fitEllipse(const std::vector<cartesian_point>& points, const cartesian_point& focus)
{
	if (points.size() != 5) {
		std::cerr << "Error: Exactly 5 points are required.\n";
		return EllipseParameters();
	}

	Eigen::MatrixXd A(5, 6);
	Eigen::VectorXd b(5);

	// Fill the matrix A and vector b with the equations from the points
	for (size_t i = 0; i < 5; ++i)
	{
		double x = points[i].x;
		double y = points[i].y;
		A(i, 0) = x * x;       // Coefficient for x^2
		A(i, 1) = x * y;       // Coefficient for xy
		A(i, 2) = y * y;       // Coefficient for y^2
		A(i, 3) = x;           // Coefficient for x
		A(i, 4) = y;           //  Coefficient for y
		A(i, 5) = 1;           // Constant term
		b(i) = -1;             // Right-hand side is -1. This is important!
	}

	// Solve for the ellipse parameters
	Eigen::VectorXd ellipseParams = A.jacobiSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);

	// Compute center of ellipse
	EllipseParameters ep = extractEllipseParameters(ellipseParams);


	global_ep.angle = ep.angle;
	global_ep.centerX = ep.centerX;
	global_ep.centerY = ep.centerY;
	global_ep.semiMajor = ep.semiMajor;
	global_ep.semiMinor = ep.semiMinor;

	//cout << global_ep.angle << endl;
	//cout << global_ep.centerX << endl;
	//cout << global_ep.centerY << endl;
	//cout << global_ep.semiMajor << endl;
	//cout << global_ep.semiMinor << endl;

	return ep;
}

P.S. I’m often wrong. If there is a glaring error in my logic then please show me the correct way. As for ellipses there are two foci of 2 coordinates each, plus a combined focal distance. Does that not count as 5 degrees of freedom? Have I been misled?

I didn't understand what problems you had with the linear-algebra approach. Here's some working C++ code, using the armadillo library for matrix operations (compile with -l armadillo).

#include <iostream>
#include <armadillo>

struct Point {
  double x, y;
};

int main() {
  Point p[] = {Point{-1.0, 0.0}, Point{1.0, 0.0}, Point{0.0, -1.0}, Point{0.0, 1.0}, Point{0.85, 0.85}, Point{0.8, 0.9}};
  const int N = sizeof(p)/sizeof(*p);
  
  arma::mat A(N,5);
  arma::vec b(N);
  for (int i = 0; i < N; ++i) {
    double x = p[i].x;
    double y = p[i].y;
    A(i,0) = x;
    A(i,1) = y;
    A(i,2) = x*x;
    A(i,3) = x*y;
    A(i,4) = y*y;
    b(i) = 1.0;
  }
  std::cout << arma::inv(A.t() * A) * (A.t() * b) << '\n';
}

This will print 5 numbers, let's call then a, b, c, d, e. The equation of your ellipse [EDIT: or hyperbola] is ax+by+cx^2+dxy+ey^2=1.

It's always nice to have an extra reference code. Thank you.

Perhaps you can make sense of this… the only way that I can get it to work is if I do the following:

	if (points.size() != 6) {
		std::cerr << "Error: Exactly 6 points are required.\n";
		return EllipseParameters();
	}

	Eigen::MatrixXd A(6, 6);
	Eigen::VectorXd b(6);

	// Fill the matrix A and vector b with the equations from the points
	for (size_t i = 0; i < 6; ++i)
	{
		double x = points[i].x;
		double y = points[i].y;
		A(i, 0) = x * x;       // Coefficient for x^2
		A(i, 1) = x * y;       // Coefficient for xy
		A(i, 2) = y * y;       // Coefficient for y^2
		A(i, 3) = x;           // Coefficient for x
		A(i, 4) = y;           //  Coefficient for y
		A(i, 5) = 1;           // Constant term
		b(i) = -1;             // Right-hand side is -1
	}

I am wondering why you use a different notation than that used on Wikipedia?

Like, they have it as $A x^2 + B xy + C y^2 + D x + E y + F = 0$.

OK, so I got it kind of working. The thing is, I get the same solution using either 6 or 5 points. I get an ellipse that is wonky… centred at the origin, which is no good. The orange ellipse is gotten by solving the system of equations, and the green ellipse is gotten from numerical integration.

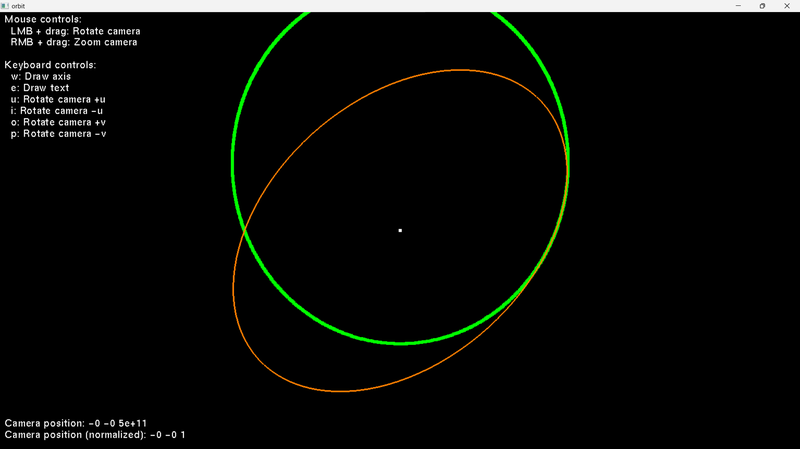
OK, I'm getting closer. The orange ellipse is the one gotten from solving the system of equations, and the green ellipse is gotten from numerical integration. So the solver is not quite correct.

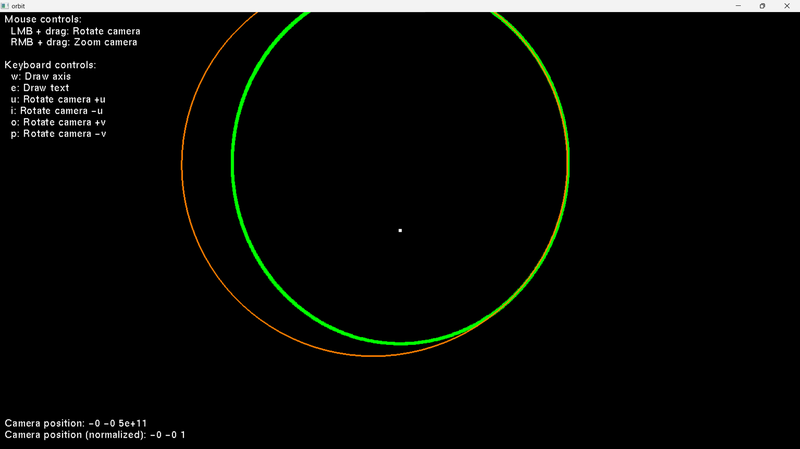
The code is:

EllipseParameters extractEllipseParameters(const Eigen::VectorXd& coefficients)
{/*
	A(i, 0) = x;
	A(i, 1) = y;
	A(i, 2) = x * x;
	A(i, 3) = x * y;
	A(i, 4) = y * y;*/

	double a = coefficients(2);
	double b = coefficients(3);
	double c = coefficients(4);
	double d = coefficients(0);
	double e = coefficients(1);
	double f = 1;

	// Calculate center
	double centerX = (2 * c * d - b * e) / (b * b - 4 * a * c);
	double centerY = (2 * a * e - b * d) / (b * b - 4 * a * c);

	// Calculate rotation angle
	double theta = 0.5 * atan2(b, (a - c));

	// Calculate semi-axes
	double ct = cos(theta);
	double st = sin(theta);
	double ct2 = ct * ct;
	double st2 = st * st;
	double a2 = a * ct2 + b * ct * st + c * st2;
	double c2 = a * st2 - b * ct * st + c * ct2;

	// Calculate constants
	double term = 2 * (a * centerX * centerX + b * centerX * centerY +
		c * centerY * centerY + d * centerX + e * centerY + f);

	double semiMajor = sqrt(abs(term / (2 * std::min(a2, c2))));
	double semiMinor = sqrt(abs(term / (2 * std::max(a2, c2))));

	if (a2 > c2) {
		std::swap(semiMajor, semiMinor);
		theta += pi / 2;
	}

	EllipseParameters params;
	params.centerX = centerX;
	params.centerY = centerY;
	params.semiMajor = semiMajor;
	params.semiMinor = semiMinor;
	params.angle = theta;

	return params;
}






EllipseParameters fitEllipse(const std::vector<cartesian_point>& points, const cartesian_point& focus)
{
	if (points.size() != 5) {
		std::cerr << "Error: Exactly 5 points are required.\n";
		return EllipseParameters();
	}

	Eigen::MatrixXd A(6, 5);
	Eigen::VectorXd b(6);

	// Fill the matrix A and vector b with the equations from the points
	for (size_t i = 0; i < 6; ++i)
	{
		double x = points[i].x;
		double y = points[i].y;

		A(i, 0) = x;
		A(i, 1) = y;
		A(i, 2) = x * x;
		A(i, 3) = 0;// x* y;
		A(i, 4) = y * y;
		b(i) = -1;
	}

	Eigen::VectorXd ellipseParams = (A.transpose() * A).ldlt().solve(A.transpose() * b);

	// Solve for the ellipse parameters
	//Eigen::VectorXd ellipseParams = A.jacobiSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);


	// Compute center of ellipse
	EllipseParameters ep = extractEllipseParameters(ellipseParams);


	global_ep.angle = ep.angle;
	global_ep.centerX = ep.centerX;
	global_ep.centerY = ep.centerY;
	global_ep.semiMajor = ep.semiMajor;
	global_ep.semiMinor = ep.semiMinor;

	return ep;
}

If I set

b(i) = 1

then I get this:

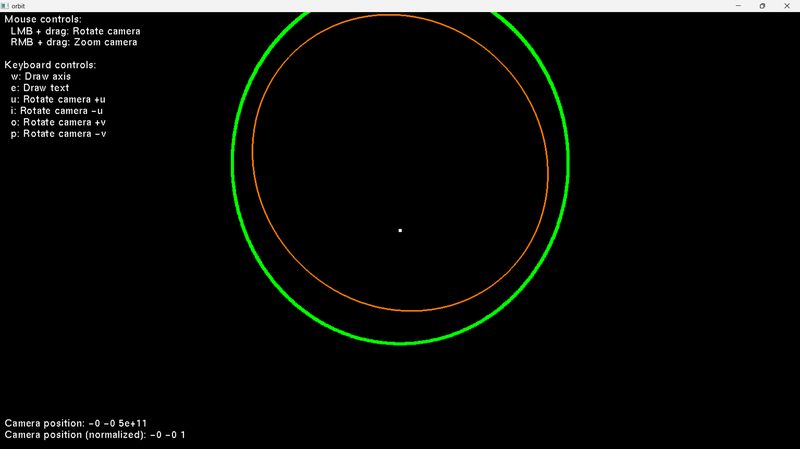
… so I'm getting closer, I think. LOL

One more misunderstanding… the fault lies with the AI and the coder, not the technique. … except for gradient descent, which inherently sucks.

Working good now that I disabled rotation and translation. Also, only 5 points were required, and b() = -1, like I said so.

if (points.size() != 5 ) {
	std::cerr << "Error: 5 points are required.\n";
	return EllipseParameters();
}

Eigen::MatrixXd A(5, 5);
Eigen::VectorXd b(5);

// Fill the matrix A and vector b with the equations from the points
for (size_t i = 0; i < 5; ++i)
{
	double x = points[i].x;
	double y = points[i].y;

	A(i, 0) = x * x;
	A(i, 1) = 0; // No rotation on x*y
	A(i, 2) = y * y;
	A(i, 3) = 0; // No translation on x
	A(i, 4) = y;

	b(i) = -1;
}

// Solve for the ellipse parameters
Eigen::VectorXd ellipseParams = A.jacobiSvd(Eigen::ComputeFullU | Eigen::ComputeFullV).solve(b);