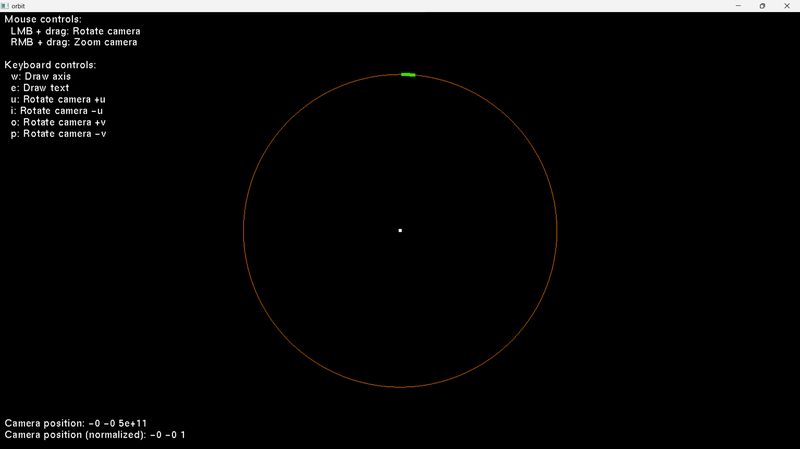
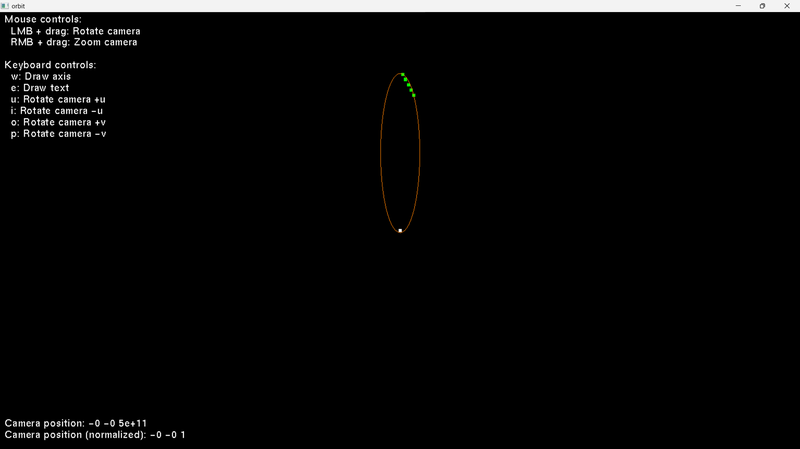
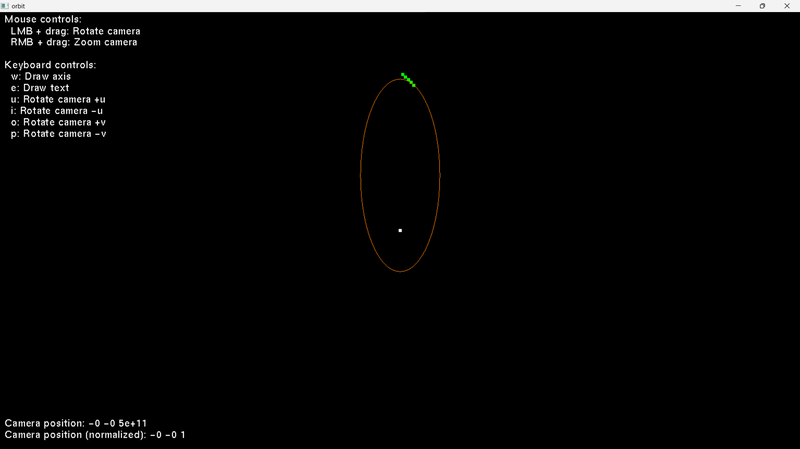
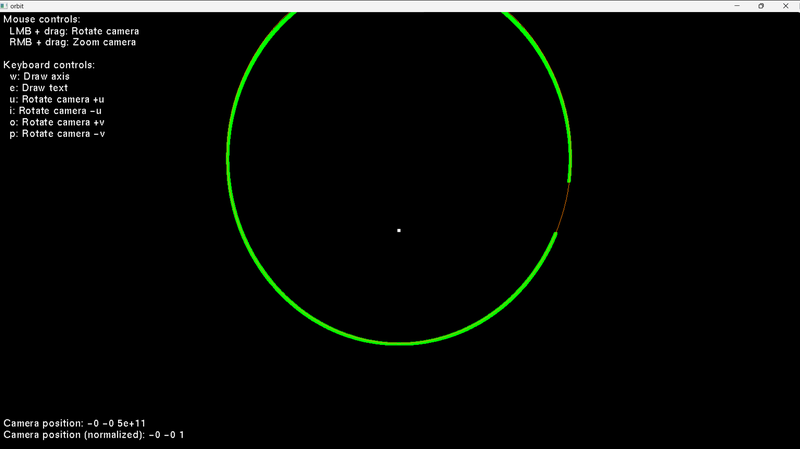
I found a solution. I was using the ellipse centre instead of the 2nd focus when calculating the distance equation. So, I calculate the 2nd focus now, and I use it.

   struct EllipseParameters2 {
       double semi_major_axis;
       double eccentricity;
       double angle;
       Eigen::Vector2d center;
   };

   // Helper function for distance calculation
   double distance(double x1, double y1, double x2, double y2) 
   {
       return sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2));
   }
   
   // Objective function for optimization (least squares)
   double objectiveFunction(
       const VectorXd& params, 
       const vector<cartesian_point>& points, 
       const vector<cartesian_point>& velocities, 
       const cartesian_point& focus) 
   {
       double h = params[0], k = params[1], a = params[2], b = params[3];
       double error = 0;
   
       EllipseParameters2 ep;
       ep.angle = 0; 
       ep.center(0) = 0;
       ep.center(1) = k;
       ep.semi_major_axis = a;
       ep.eccentricity = sqrt(1 - (b * b) / (a * a));
   
       Eigen::Vector2d focus1;
       focus1(0) = focus.x;
       focus1(1) = focus.y;
   
       Eigen::Vector2d focus2 = calculateSecondFocus(ep, focus1);
    
       for(size_t i = 0; i < points.size(); i++)
       {
           cartesian_point p = points[i];
           cartesian_point v = velocities[i];
   
           double dist1 = distance(p.x, p.y,  focus1(0),  focus1(1));
           double dist2 = distance(p.x, p.y,  focus2(0),  focus2(1));
   
           error += pow(dist1 + dist2 - 2 * a, 2);
   
           // Since we're axis-aligned, we simplify velocity condition:
           // Velocity should be more in line with the axis of the ellipse
           double velError = 0;
   
           if (abs(v.x) > abs(v.y)) // Suggesting a is along x
               velError = pow(v.y / v.x - (k - p.y) / (h - p.x), 2); // Check alignment with y
           else
               velError = pow(v.x / v.y - (h - p.x) / (k - p.y), 2); // Check alignment with x
   
           error += velError;
       }
   
       return error;
   }

Also, I tweaked how the gradient descent initial parameters are set.

   // Simple solver function using gradient descent (for demonstration)
   VectorXd solveEllipseParameters(const vector<cartesian_point>& points, const vector<cartesian_point>& velocities, const cartesian_point& focus)
   {
       // Get max distance data
       vector<double> mvec;
   
       mvec.push_back(points[0].length());
       mvec.push_back(points[1].length());
       mvec.push_back(points[2].length());
       mvec.push_back(points[3].length());
       mvec.push_back(points[4].length());
   
       sort(mvec.begin(), mvec.end());
   
       // Use the maximum distance data
       const double m = mvec[4];
   
       const double d = (mvec[4] - mvec[0]) / mvec[4];
       
       VectorXd params(4); // h, k, a, b
   
       cout << "d: " << d << endl;
   
       if(d < 0.1)
       params << 1, 1, m, m; // Initial guess
       else
       params << 1, 1, m*0.125, m*0.125; // Initial guess
   
   
       int iterations = 100000;
       double stepSize = 0.0001;
   
       for (int i = 0; i < iterations; i++) 
       {
           VectorXd gradient = VectorXd::Zero(4);
   
           for (int j = 0; j < 4; j++) 
           {
               VectorXd paramsPlus = params;
               paramsPlus[j] += stepSize;
               VectorXd paramsMinus = params;
               paramsMinus[j] -= stepSize;
               
               gradient[j] = (objectiveFunction(paramsPlus, points, velocities, focus) - objectiveFunction(paramsMinus, points, velocities, focus)) / (2 * stepSize);
           }
   
           params -= stepSize * gradient;
       }
   
       return params;
   }

The results are not quite perfect, but they're closer. Any suggestions on how to better go about calculating the initial parameters for the gradient descent are very welcome.

I fixed the problematic setting of initial guesses for the gradient descent. Works great!

VectorXd solveEllipseParameters(const vector<cartesian_point>& points, const vector<cartesian_point>& velocities, const cartesian_point& focus)
{
	// Get max distance data
	vector<double> mvec;

	mvec.push_back(points[0].length());
	mvec.push_back(points[1].length());
	mvec.push_back(points[2].length());
	mvec.push_back(points[3].length());
	mvec.push_back(points[4].length());

	sort(mvec.begin(), mvec.end());

	// Use the maximum distance data	
	const double m = mvec[4];
		
	double d = (mvec[4] - mvec[0]) / mvec[4];
	d = pow(1 - d, 20.0);

	VectorXd params(4); // h, k, a, b
	params << 1, 1, m * d, m * d; // Initial guess

	int iterations = 1000;
	double stepSize = 0.0001;

	for (int i = 0; i < iterations; i++)
	{
		VectorXd gradient = VectorXd::Zero(4);

		for (int j = 0; j < 4; j++)
		{
			VectorXd paramsPlus = params;
			paramsPlus[j] += stepSize;
			VectorXd paramsMinus = params;
			paramsMinus[j] -= stepSize;

			gradient[j] = (objectiveFunction(paramsPlus, points, velocities, focus) - objectiveFunction(paramsMinus, points, velocities, focus)) / (2 * stepSize);
		}

		params -= stepSize * gradient;
	}

	return params;
}

I’ve been using ChatGPT, Grok, Copilot, and Claude. I carefully studied their output, when it came to solving for the ellipse parameters using both gradient descent, and Jacobi SVD. The ellipse that it solves for is not really similar to the ellipse gotten via numerical integration of position and velocity using 4th-order symplectic solver.

The AI is amazing in so many ways, but in the end, it fails.

taby said:
The AI is amazing in so many ways, but in the end, it fails.

Not anymore.

You did post your solution on githib, no? ; )

I did. LOL There's a lot of good code in there though, like converting an angle-time coordinate into Cartesian coordinates and velocity → https://github.com/sjhalayka/ellipse_fitting

But in the end, Jacobi SVD and gradient descent are both numerical solutions that don't really work. If we're going to use a numerical solution, then we might as well just track the orbit based on the input position and velocity, using symplectic integration. Gathering the angle, semi-major axis and semi-minor axis, and the centre from the orbit data would be pretty straightforward. If we demand that we use a numerical method, then the orbit tracking is the best bang for the buck.

I finally found an analytical solution to the ellipse fitting problem. Basically, the person who asked the question on Physics Stack Exchange said that they had already tried the AIs to generate the necessary code. Well, I finally found the answer using Meta AI. The instructions that I gave were “how do i use gauss's method with three input points for orbit ellipse center, semi-major axis, and semi minor axis determination. please use c++. use heliocentric position. use equatorial plane for orbit. don't forget v2.”

So I wasted all that time on numerical solutions. :)

The answer and GitHub are both up-to-date: 

https://physics.stackexchange.com/a/839919/142234

https://github.com/sjhalayka/ellipse_fitting

A point belonging to an ellipse can be described as a linear combination of 1, x, y, x^2, xy and y^2 being zero. You can fix the coefficient for 1 to 1 and fit the others, using least squares regression. This should be fast and robust.

I tried solving for the ellipse coefficients (A, B, C, D, E, F) and / or parameters (centre, axes, angle) using Jacobi SVD and gradient descent. Both looked nice, but neither was an actual close answer. I now know a lot more about linear algebra, even though the project failed. For what it's worth, when solving Mx = b, I had to set b's elements to -1, not zero.

taby said:
For what it's worth, when solving Ax = b, I had to set b's elements to -1, not zero.

That's definitely why it failed. When setting up the system it should look like this:

A: numPoints * numCoefficients
x: numCoefficients * 1
b: numPoints * 1

A:
[ 1 x0 y0 x0*x0 x0*y0 y0*y0 ]
[ 1 x1 y1 x1*x1 x1*y1 y1*y1 ]
[ .... ]
[ 1 xN yN xN*xN xN*yN yN*yN ]

b:
[ 0 ]
[ ... ]
[ 0 ]

You also will need at least as many points as coefficients, or else the system is underdetermined. Once you set up the system as above, it should just be a simple least squares solve, no gradient descent or iterative algorithms required.

https://en.wikipedia.org/wiki/Ellipse#General_ellipse

No, I’ve made you misunderstand. It worked insomuch that it found an ellipse based on the 5 input points and 5 input velocities and one focus.. It looks close on the screen, but It’s just not close enough. It’s a failure.