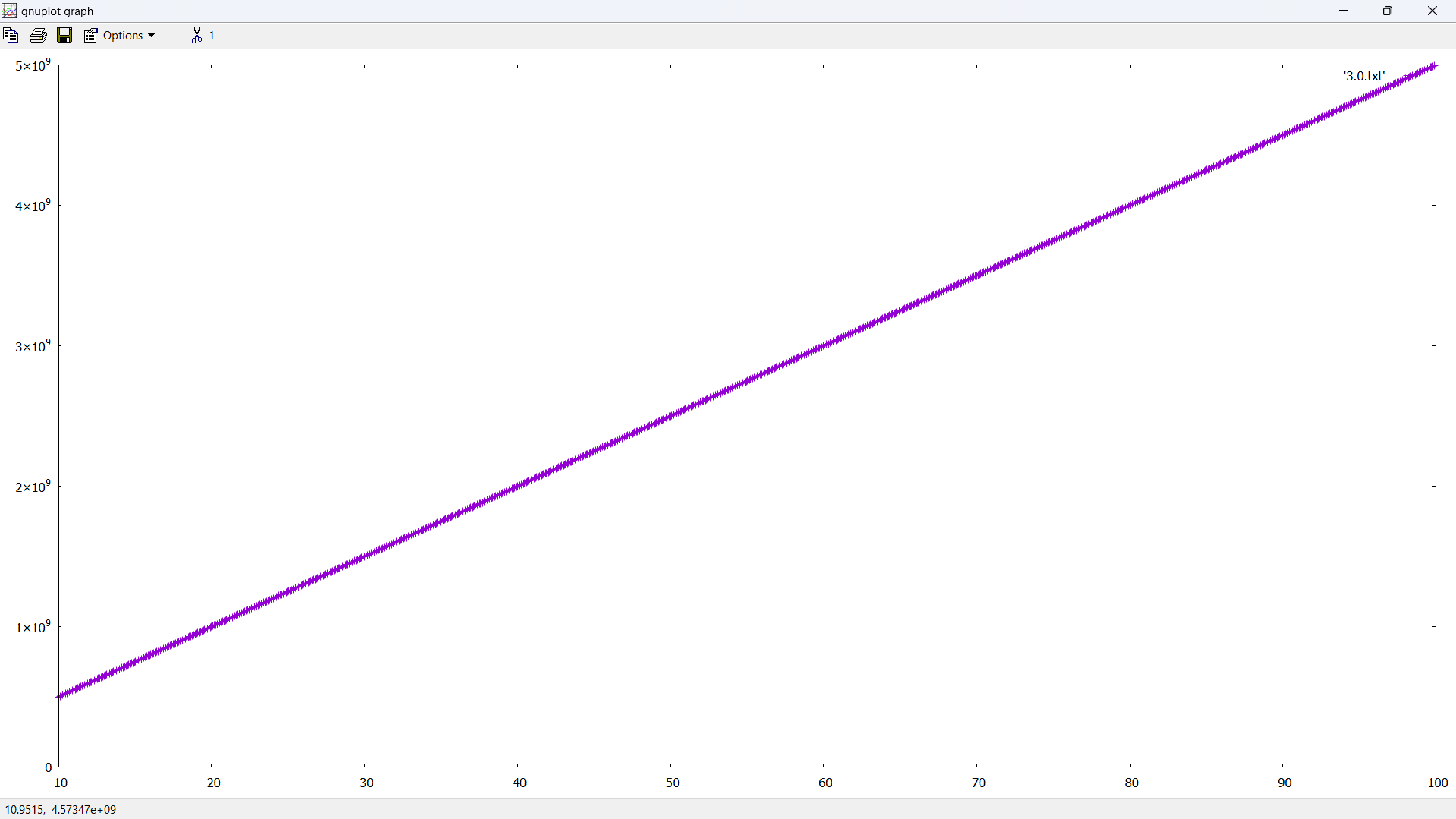
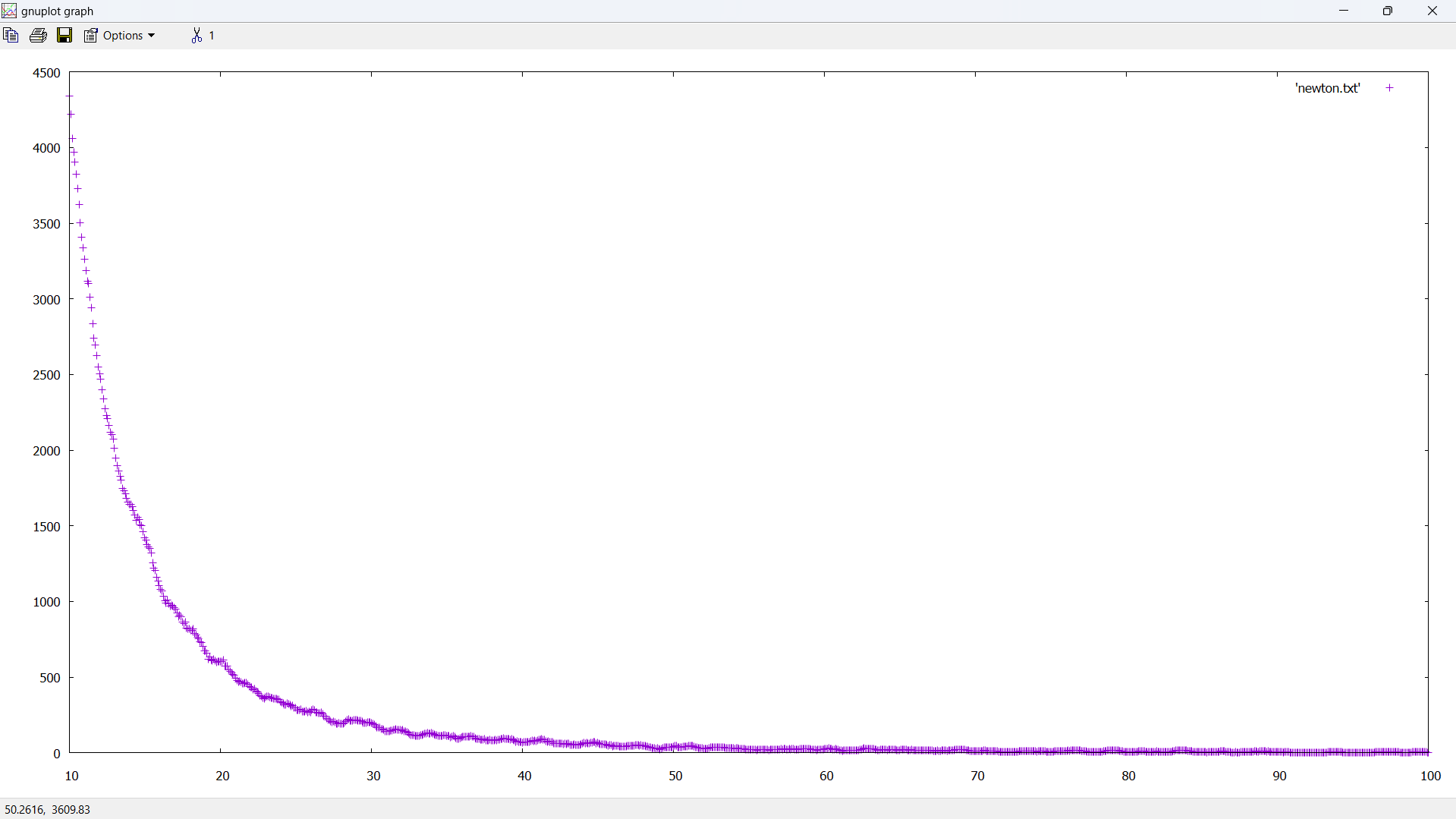
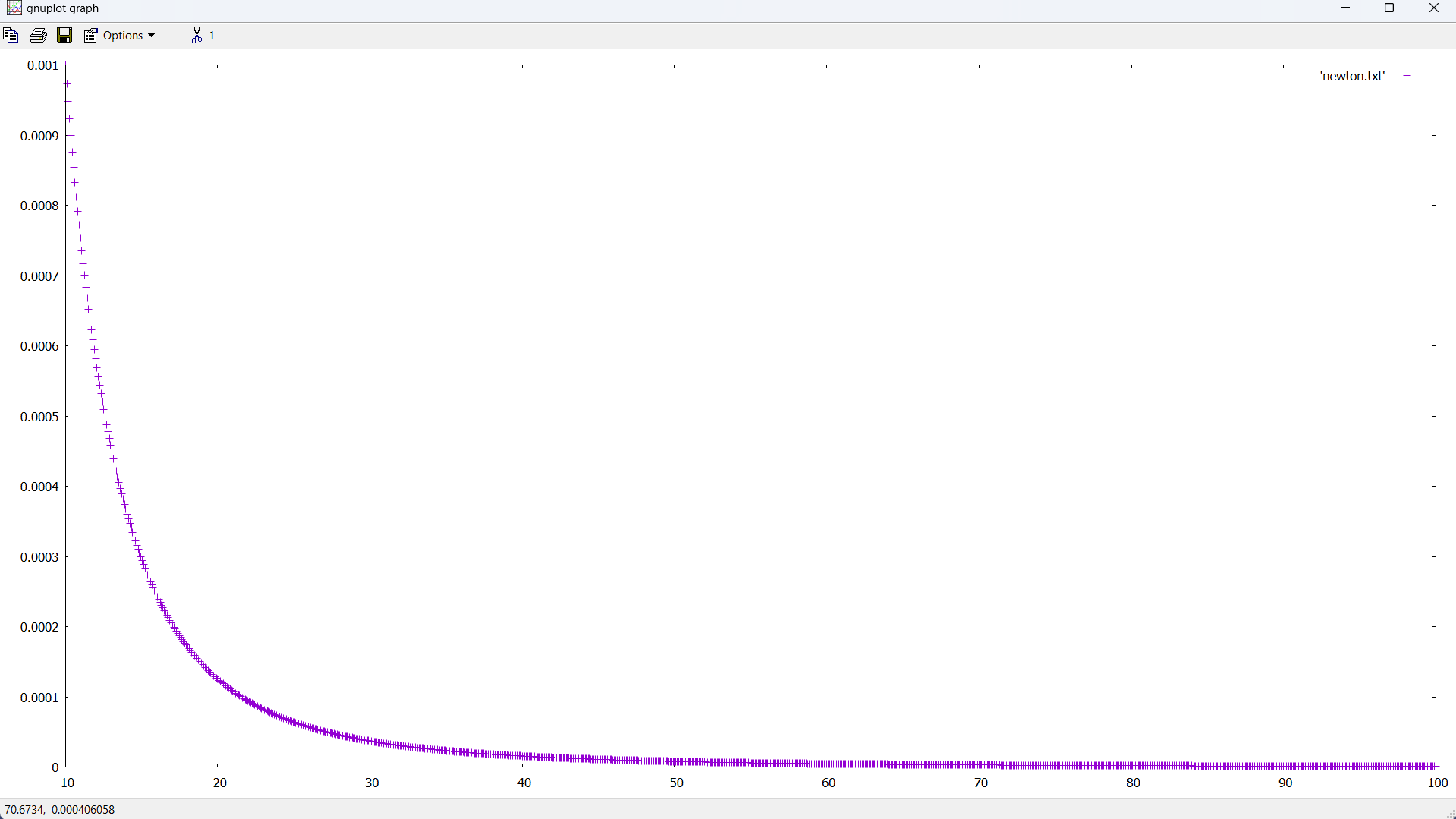
OK, so I have it drawing a straight line. I'm closer:
#include "main.h"
real_type get_intersecting_line_count(
size_t n,
const vector_3 sphere_location,
const real_type sphere_radius)
{
real_type spherical_cap_area = 2.0 * pi * sphere_radius * sphere_location.x;
real_type sphere_area = 4.0 * pi * sphere_location.x * sphere_location.x;
real_type ratio = spherical_cap_area / sphere_area;
return (static_cast<real_type>(n) * ratio);
}
int main(int argc, char** argv)
{
//cout << setprecision(10);
const size_t n = 100000000; // Oscillator count
string filename = "3.0.txt";
ofstream out_file(filename.c_str());
out_file << setprecision(30);
const real_type start_distance = 10;
const real_type end_distance = 100;
const size_t distance_res = 1000;
const real_type distance_step_size = (end_distance - start_distance) / (distance_res - 1);
for (real_type r = start_distance; r <= end_distance; r += distance_step_size)
{
const vector_3 receiver_pos(r, 0, 0);
const real_type receiver_radius = 1.0;
const real_type epsilon = 0.01;
// https://en.wikipedia.org/wiki/Directional_derivative
const vector_3 receiver_pos_plus(receiver_pos.x + epsilon, 0, 0);
const real_type collision_count_plus = get_intersecting_line_count(n, receiver_pos_plus, receiver_radius);
const real_type collision_count = get_intersecting_line_count(n, receiver_pos, receiver_radius);
const vector_3 gradient((collision_count_plus - collision_count) / epsilon, 0, 0);
const real_type gradient_strength = gradient.length() * pow(receiver_pos.length(), 3.0);
cout << "r: " << r << " " << gradient_strength << endl;
out_file << r << " " << gradient_strength << endl;
}
out_file.close();
return 0;
}