What exactly is an Octree? If you're completely unfamiliar with them, I recommend reading the Wikipedia article (read time: ~5 minutes). This is a sufficient description of what it is but is barely enough to give any ideas on what it's used for and how to actually implement one. In this article, I will do my best to take you through the steps necessary to create an octree data structure through conceptual explanations, pictures, and code, and show you the considerations to be made at each step along the way. I don't expect this article to be the authoritative way to do octrees, but it should give you a really good start and act as a good reference.
Assumptions
Before we dive in, I'm going to be making a few assumptions about you as a reader:
- You are very comfortable with programming in a C-syntax-style language (I will be using C# with XNA).
- You have programmed some sort of tree-like data structure in the past, such as a binary search tree and are familiar with recursion and its strengths and pitfalls.
- You know how to do collision detection with bounding rectangles, bounding spheres, and bounding frustums.
- You have a good grasp of common data structures (arrays, lists, etc) and understand Big-O notation (you can also learn about Big-O in this GDnet article).
- You have a development environment project which contains spatial objects which need collision tests.
Setting the stage
Let's suppose that we are building a very large game world which can contain thousands of physical objects of various types, shapes and sizes, some of which must collide with each other. Each frame we need to find out which objects are intersecting with each other and have some way to handle that intersection. How do we do it without killing performance?
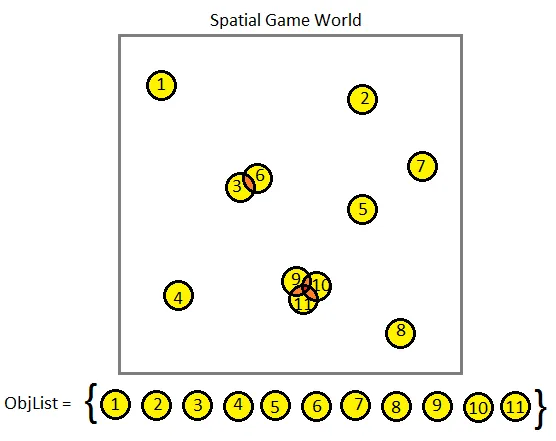
Brute force collision detection
The simplest method is to just compare each object against every other object in the world. Typically, you can do this with two for loops. The code would look something like this:
foreach(gameObject myObject in ObjList)
{
foreach(gameObject otherObject in ObjList)
{
if(myObject == otherObject) continue; //avoid self collision check
if(myObject.CollidesWith(otherObject))
{
//code to handle the collision
}
}
}
Conceptually, this is what we're doing in our picture:
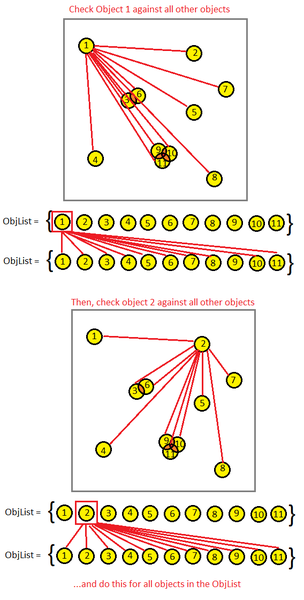
Each red line is an expensive CPU test for intersection. Naturally, you should feel horrified by this code because it is going to run in O(N^2) time. If you have 10,000 objects, then you're going to be doing 100,000,000 collision checks (hundred million). I don't care how fast your CPU is or how well you've tuned your math code, this code would reduce your computer to a sluggish crawl. If you're running your game at 60 frames per second, you're looking at 60 * 100 million calculations per second! It's nuts. It's insane. It's crazy. Let's not do this if we can avoid it, at least not with a large set of objects. This would only be acceptable if we're only checking, say, 10 items against each other (100 checks is palatable). If you know in advance that your game is only going to have a very small number of objects (i.e., Asteroids), you can probably get away with using this brute force method for collision detection and ignore octrees altogether. If/when you start noticing performance problems due to too many collision checks per frame, consider some simple targeted optimizations:
- How much computation does your current collision routine take? Do you have a square root hidden away in there (ie, a distance check)? Are you doing a granular collision check (pixel vs pixel, triangle vs triangle, etc)? One common technique is to perform a rough, coarse check for collision before testing for a granular collision check. You can give your objects an enclosing bounding rectangle or bounding sphere and test for intersection with these before testing against a granular check which may involve a lot more math and computation time. Quote
Use a "distance squared" check for comparing distance between objects to avoid using the square root method. Square root calculation typically uses the newtonian method of approximation and can be computationally expensive.
- Can you get away with calculating fewer collision checks? If your game runs at 60 frames per second, could you skip a few frames? If you know certain objects behave deterministically, can you "solve" for when they will collide ahead of time (ie, pool ball vs. side of pool table). Can you reduce the number of objects which need to be checked for collisions? A technique for this would be to separate objects into several lists. One list could be your "stationary" objects list. They never have to test for collision against each other. The other list could be your "moving" objects, which need to be tested against all other moving objects and against all stationary objects. This could reduce the number of necessary collision tests to reach an acceptable performance level.
- Can you get away with removing some object collision tests when performance becomes an issue? For example, a smoke particle could interact with a surface object and follow its contours to create a nice aesthetic effect, but it wouldn't break gameplay if you hit a predefined limit for collision checks and decided to stop ignoring smoke particles for collision. Ignoring essential game object movement would certainly break gameplay though (i.e., player bullets stop intersecting with monsters). So, perhaps maintaining a priority list of collision checks to compute would help. First, you handle the high priority collision tests, and if you're not at your threshold, you can handle lower priority collision tests. When the threshold is reached, you dump the rest of the items in the priority list or defer them for testing at a later time.
- Can you use a faster but still simplistic method for collision detection to get away from an O(N^2) runtime? If you eliminate the objects you've already checked for collisions against, you can reduce the runtime to O(N(N+1)/2), which is much faster and still easy to implement. (technically, it's still O(N^2)) In terms of software engineering, you may end up spending more time than it's worth fine-tuning a bad algorithm & data structure choice to squeeze out a few more ounces of performance. The cost vs. benefit ratio becomes increasingly unfavourable and it becomes time to choose a better data structure to handle collision detection. Spatial partitioning algorithms are the proverbial nuke to solving the runtime problem for collision detection. At a small upfront cost to performance, they'll reduce your collision detection tests to logarithmic runtime. The upfront costs of development time and CPU overhead are easily outweighed by the scalability benefits and performance gains.
Conceptual background on spatial partitioning
Let's take a step back and look at spatial partitioning and trees in general before diving into Octrees. If we don't understand the conceptual idea, we have no hope of implementing it by sweating over the code. Looking at the brute force implementation above, we're essentially taking every object in the game and comparing their positions against all other objects in the game to see if any are touching. All of these objects are contained spatially within our game world. Well, if we create an enclosing box around our game world and figure out which objects are contained within this enclosing box, then we've got a region of space with a list of contained objects within it. In this case, it would contain every object in the game.
We can notice that if we have an object on one corner of the world and another object way on the other side, we don't really need to, or want to, calculate a collision check against them every frame. It'd be a waste of precious CPU time.
So, let's try something interesting! If we divide our world exactly in half, we can create three separate lists of objects. The first list of objects, List A, contains all objects on the left half of the world. The second list, List B, contains objects on the right half of the world. Some objects may touch the dividing line such that they're on each side of the line, so we'll create a third list, List C, for these objects.
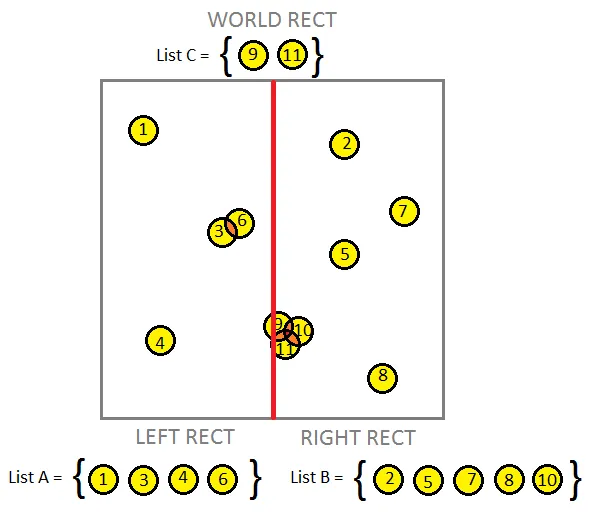
We can notice that with each subdivision, we're spatially reducing the world in half and collecting a list of objects in that resulting half. We can elegantly create a binary search tree to contain these lists. Conceptually, this tree should look something like so:
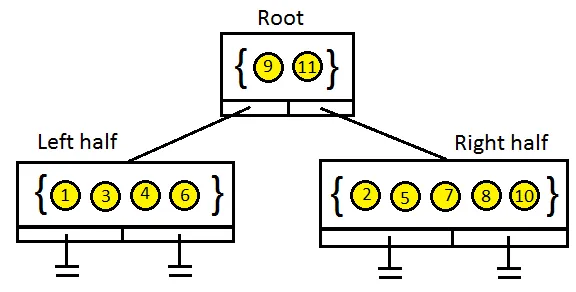
In terms of pseudo code, the tree data structure would look something like this:
public class BinaryTree
{
//This is a list of all of the objects contained within this node of the tree
private List m_objectList;
//These are pointers to the left and right child nodes in the tree
private BinaryTree m_left, m_right;
//This is a pointer to the parent object (for upward tree traversal).
private BinaryTree m_parent;
}We know that all objects in List A will never intersect with any objects in List B, so we can almost eliminate half of the number of collision checks. We've still got the objects in List C which could touch objects in either list A or B, so we'll have to check all objects in List C against all objects in Lists A, B & C. If we continue to sub-divide the world into smaller and smaller parts, we can further reduce the number of necessary collision checks by half each time. This is the general idea behind spatial partitioning. There are many ways to subdivide a world into a tree-like data structure (BSP trees, Quad Trees, K-D trees, OctTrees, etc).
Now, by default, we're just assuming that the best division is a cut in half, right down the middle, since we're assuming that all of our objects will be somewhat uniformly distributed throughout the world. It's not a bad assumption to make, but some spatial division algorithms may decide to make a cut such that each side has an equal amount of objects (a weighted cut) so that the resulting tree is more balanced. However, what happens if all of these objects move around? In order to maintain a nearly even division, you'd have to either shift the splitting plane or completely rebuild the tree each frame. It'd be a bit of a mess with a lot of complexity. So, for my implementation of a spatial partitioning tree, I decided to cut right down the middle every time. As a result, some trees may end up being a bit more sparse than others, but that's okay -- it doesn't cost much.
To subdivide or not to subdivide? That is the question.
Let's assume that we have a somewhat sparse region with only a few objects. We could continue subdividing our space until we've found the smallest possible enclosing area for that object. But is that really necessary? Let's remember that the whole reason we're creating a tree is to reduce the number of collision checks we need to perform each frame -- not to create a perfectly enclosing region of space for every object. Here are the rules I use for deciding whether to subdivide or not:
- If we create a subdivision which only contains one object, we can stop subdividing even though we could keep dividing further. This rule will become an important part of the criteria for what defines a "leaf node" in our octree.
- The other important criteria is to set a minimum size for a region. If you have an extremely small object which is nanometers in size (or, god forbid, you have a bug and forgot to initialize an object size!), you're going to keep subdividing to the point where you potentially overflow your call stack. For my own implementation, I defined the smallest containing region to be a 1x1x1 cube. Any objects in this teeny cube will just have to be run with the O(N^2) brute force collision test (I don't anticipate many objects anyways!).
- If a containing region doesn't contain any objects, we shouldn't try to include it in the tree.
We can take our subdivision by half one step further and divide the 2D world space into quadrants. The logic is essentially the same, but now we're testing for collision with four squares instead of two rectangles. We can continue subdividing each square until our rules for termination are met. The representation of the world space and corresponding data structure for a quadtree would look something like this:
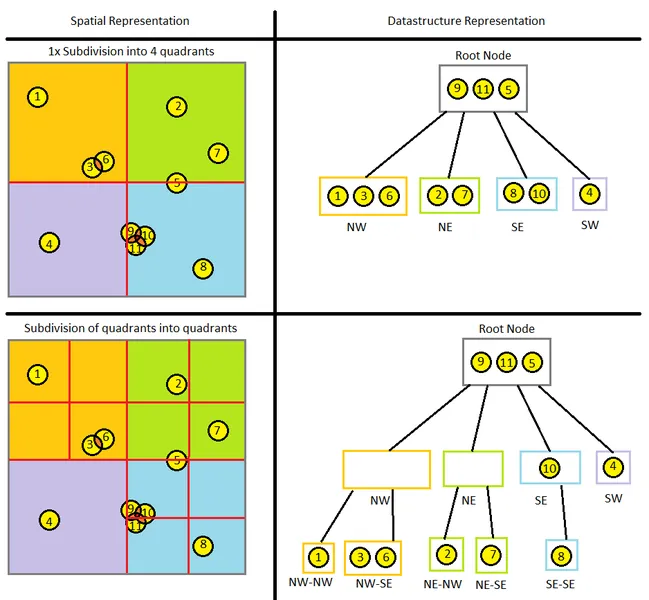
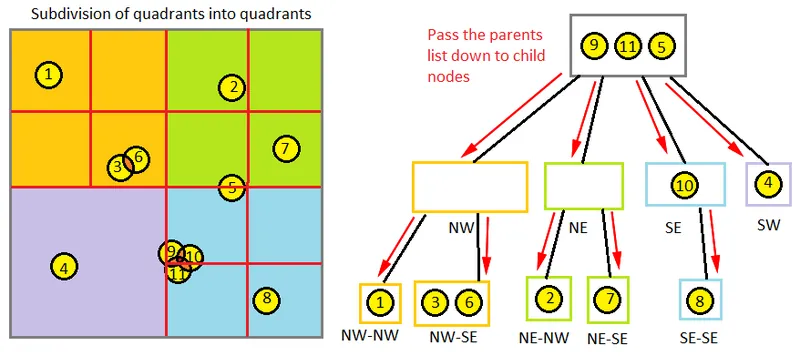
If the quadtree subdivision and data structure makes sense, then an octree should be pretty straightforward as well. We're just adding a third dimension, using bounding cubes instead of bounding squares, and have eight possible child nodes instead of four. Some of you might wonder what should happen if you have a game world with non-cubic dimensions, say 200x300x400. You can still use an octree with cubic dimensions -- some child nodes will just end up empty if the game world doesn't have anything there. Obviously, you'll want to set the dimensions of your octree to at least the largest dimension of your game world.
Octree Construction
So, as you've read, an octree is a special type of subdividing tree commonly used for objects in 3D space (or anything with 3 dimensions). Our enclosing region is going to be a three dimensional rectangle (commonly a cube). We will then apply our subdivision logic above, and cut our enclosing region into eight smaller rectangles. If a game object completely fits within one of these subdivided regions, we'll push it down the tree into that node's containing region. We'll then recursively continue subdividing each resulting region until one of our breaking conditions is met. In the end, we should expect to have a nice tree-like data structure.
My implementation of the octree can contain objects which have either a bounding sphere and/or a bounding rectangle. You'll see a lot of code I use to determine which is being used.
In terms of our Octree class data structure, I decided to do the following for each tree:
- Each node has a bounding region which defines the enclosing region
- Each node has a reference to the parent node
- Contains an array of eight child nodes (use arrays for code simplicity and cache performance)
- Contains a list of objects contained within the current enclosing region
- I use a byte-sized bitmask for figuring out which child nodes are actively being used (the optimization benefits at the cost of additional complexity is somewhat debatable)
- I use a few static variables to indicate the state of the tree
Here is the code for my Octree class outline:
public class OctTree
{
BoundingBox m_region;
List m_objects;
///
/// These are items which we're waiting to insert into the data structure.
/// We want to accrue as many objects in here as possible before we inject them into the tree. This is slightly more cache friendly.
///
static Queue m_pendingInsertion = new Queue();
///
/// These are all of the possible child octants for this node in the tree.
///
OctTree[] m_childNode = new OctTree[8];
///
/// This is a bitmask indicating which child nodes are actively being used.
/// It adds slightly more complexity, but is faster for performance since there is only one comparison instead of 8.
///
byte m_activeNodes = 0;
///
/// The minumum size for enclosing region is a 1x1x1 cube.
///
const int MIN_SIZE = 1;
///
/// this is how many frames we'll wait before deleting an empty tree branch. Note that this is not a constant. The maximum lifespan doubles
/// every time a node is reused, until it hits a hard coded constant of 64
///
int m_maxLifespan = 8; //
int m_curLife = -1; //this is a countdown time showing how much time we have left to live
///
/// A reference to the parent node is nice to have when we're trying to do a tree update.
///
OctTree _parent;
static bool m_treeReady = false; //the tree has a few objects which need to be inserted before it is complete
static bool m_treeBuilt = false; //there is no pre-existing tree yet.
}
Initializing the enclosing region
The first step in building an octree is to define the enclosing region for the entire tree. This will be the bounding box for the root node of the tree which initially contains all objects in the game world. Before we go about initializing this bounding volume, we have a few design decisions we need to make:
- What should happen if an object moves outside of the bounding volume of the root node? Do we want to resize the entire octree so that all objects are enclosed? If we do, we'll have to completely rebuild the octree from scratch. If we don't, we'll need to have some way to either handle out of bounds objects or ensure that objects never go out of bounds.
- How do we want to create the enclosing region for our octree? Do we want to use a preset dimension, such as a 200x400x200 (X,Y,Z) rectangle? Or do we want to use a cubic dimension which is a power of 2? What should be the smallest allowable enclosing region which cannot be subdivided?
Personally, I decided that I would use a cubic enclosing region with dimensions which are a power of 2, and sufficiently large to completely enclose my world. The smallest allowable cube is a 1x1x1 unit region. With this, I know that I can always cleanly subdivide my world and get integer numbers (even though the Vector3 uses floats). I also decided that my enclosing region would enclose the entire game world, so if an object leaves this region, it should be quietly destroyed. At the smallest octant, I will have to run a brute force collision check against all other objects, but I don't realistically expect more than 3 objects to occupy that small of an area at a time, so the performance costs of O(N^2) are completely acceptable. So, I normally just initialize my octree with a constructor which takes a region size and a list of items to insert into the tree. I feel it's barely worth showing this part of the code since it's so elementary, but I'll include it for completeness. Here are my constructors:
/*Note: we want to avoid allocating memory for as long as possible since there can be lots of nodes.*/
///
/// Creates an oct tree which encloses the given region and contains the provided objects.
///
///The bounding region for the oct tree.
///The list of objects contained within the bounding region
private OctTree(BoundingBox region, List objList)
{
m_region = region;
m_objects = objList;
m_curLife = -1;
}
public OctTree()
{
m_objects = new List();
m_region = new BoundingBox(Vector3.Zero, Vector3.Zero);
m_curLife = -1;
}
///
/// Creates an octTree with a suggestion for the bounding region containing the items.
///
///The suggested dimensions for the bounding region.
///Note: if items are outside this region, the region will be automatically resized.
public OctTree(BoundingBox region)
{
m_region = region;
m_objects = new List();
m_curLife = -1;
} Building an initial octree
I'm a big fan of lazy initialization. I try to avoid allocating memory or doing work until I absolutely have to. In the case of my octree, I avoid building the data structure as long as possible. We'll accept a user's request to insert an object into the data structure, but we don't actually have to build the tree until someone runs a query against it.
What does this do for us? Well, let's assume that the process of constructing and traversing our tree is somewhat computationally expensive. If a user wants to give us 1,000 objects to insert into the tree, does it make sense to recompute every subsequent enclosing area a thousand times? Or, can we save some time and do a bulk blast? I created a "pending" queue of items and a few flags to indicate the build state of the tree. All of the inserted items get put into the pending queue and when a query is made, those pending requests get flushed and injected into the tree. This is especially handy during a game loading sequence since you'll most likely be inserting thousands of objects at once. After the game world has been loaded, the number of objects injected into the tree is orders of magnitude fewer. My lazy initialization routine is contained within my UpdateTree() method. It checks to see if the tree has been built, and builds the data structure if it doesn't exist and has pending objects.
///
/// Processes all pending insertions by inserting them into the tree.
///
/// Consider deprecating this?
private void UpdateTree() //complete & tested
{
if (!m_treeBuilt)
{
while (m_pendingInsertion.Count != 0)
m_objects.Add(m_pendingInsertion.Dequeue());
BuildTree();
}
else
{
while (m_pendingInsertion.Count != 0)
Insert(m_pendingInsertion.Dequeue());
}
m_treeReady = true;
} As for building the tree itself, this can be done recursively. So for each recursive iteration, I start off with a list of objects contained within the bounding region. I check my termination rules, and if we pass, we create eight subdivided bounding areas which are perfectly contained within our enclosed region. Then, I go through every object in my given list and test to see if any of them will fit perfectly within any of my octants. If they do fit, I insert them into a corresponding list for that octant. At the very end, I check the counts on my corresponding octant lists and create new octrees and attach them to our current node, and mark my bitmask to indicate that those child octants are actively being used. All of the leftover objects have been pushed down to us from our parent, but can't be pushed down to any children, so logically, this must be the smallest octant which can contain the object.
///
/// Naively builds an oct tree from scratch.
///
private void BuildTree() //complete & tested
{
//terminate the recursion if we're a leaf node
if (m_objects.Count <= 1)
return;
Vector3 dimensions = m_region.Max - m_region.Min;
if (dimensions == Vector3.Zero)
{
FindEnclosingCube();
dimensions = m_region.Max - m_region.Min;
}
//Check to see if the dimensions of the box are greater than the minimum dimensions
if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE)
{
return;
}
Vector3 half = dimensions / 2.0f;
Vector3 center = m_region.Min + half;
//Create subdivided regions for each octant
BoundingBox[] octant = new BoundingBox[8];
octant[0] = new BoundingBox(m_region.Min, center);
octant[1] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z));
octant[2] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z));
octant[3] = new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z));
octant[4] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z));
octant[5] = new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z));
octant[6] = new BoundingBox(center, m_region.Max);
octant[7] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z));
//This will contain all of our objects which fit within each respective octant.
List[] octList = new List[8];
for (int i = 0; i < 8; i++)
octList = new List();
//this list contains all of the objects which got moved down the tree and can be delisted from this node.
List delist = new List();
foreach (Physical obj in m_objects)
{
if (obj.BoundingBox.Min != obj.BoundingBox.Max)
{
for (int a = 0; a < 8; a++)
{
if (octant[a].Contains(obj.BoundingBox) == ContainmentType.Contains)
{
octList[a].Add(obj);
delist.Add(obj);
break;
}
}
}
else if (obj.BoundingSphere.Radius != 0)
{
for (int a = 0; a < 8; a++)
{
if (octant[a].Contains(obj.BoundingSphere) == ContainmentType.Contains)
{
octList[a].Add(obj);
delist.Add(obj);
break;
}
}
}
}
//delist every moved object from this node.
foreach (Physical obj in delist)
m_objects.Remove(obj);
//Create child nodes where there are items contained in the bounding region
for (int a = 0; a < 8; a++)
{
if (octList[a].Count != 0)
{
m_childNode[a] = CreateNode(octant[a], octList[a]);
m_activeNodes |= (byte)(1 << a);
m_childNode[a].BuildTree();
}
}
m_treeBuilt = true;
m_treeReady = true;
}
private OctTree CreateNode(BoundingBox region, List objList) //complete & tested
{
if (objList.Count == 0)
return null;
OctTree ret = new OctTree(region, objList);
ret._parent = this;
return ret;
}
private OctTree CreateNode(BoundingBox region, Physical Item)
{
List objList = new List(1); //sacrifice potential CPU time for a smaller memory footprint
objList.Add(Item);
OctTree ret = new OctTree(region, objList);
ret._parent = this;
return ret;
}Updating a tree
Let's imagine that our tree has a lot of moving objects in it. If any object moves, there is a good chance that the object has moved outside of its enclosing octant. How do we handle changes in object position while maintaining the integrity of our tree structure?
Technique 1: Keep it super simple, trash & rebuild everything.
Some implementations of an Octree will completely rebuild the entire tree every frame and discard the old one. This is super simple and it works, and if this is all you need, then prefer the simple technique. The general consensus is that the upfront CPU cost of rebuilding the tree every frame is much cheaper than running a brute force collision check, and programmer time is too valuable to be spent on an unnecessary optimization. For those of us who like challenges and to over-engineer things, the "trash & rebuild" technique comes with a few small problems:
- You're constantly allocating and deallocating memory each time you rebuild your tree. Allocating new memory comes at a small cost. If possible, you want to minimize the amount of memory being allocated and reallocated over time by reusing memory you've already got.
- Most of the tree is unchanging, so it's a waste of CPU time to rebuild the same branches over and over again.
Technique 2: Keep the existing tree, update the changed branches
I noticed that most branches of a tree don't need to be updated. They just contain stationary objects. Wouldn't it be nice if, instead of rebuilding the entire tree every frame, we just updated the parts of the tree which needed an update? This technique keeps the existing tree and updates only the branches which had an object which moved. It's a bit more complex to implement, but it's a lot more fun too, so let's really get into that!
During my first attempt at this, I mistakenly thought that an object in a child node could only go up or down one traversal of the tree. This is wrong. If an object in a child node reaches the edge of that node, and that edge also happens to be an edge for the enclosing parent node, then that object needs to be inserted above its parent, and possibly up even further. So, the bottom line is that we don't know how far up an object needs to be pushed up the tree. Just as well, an object can move such that it can be neatly enclosed in a child node, or that child's child node. We don't know how far down the tree we can go.
Fortunately, since we include a reference to each node's parent, we can easily solve this problem recursively with minimal computation! The general idea behind the update algorithm is to first let all objects in the tree update themselves. Some may move or change in size. We want to get a list of every object which moved, so the object update method should return to us a boolean value indicating if its bounding area changed. Once we've got a list of all of our moved objects, we want to start at our current node and try to traverse up the tree until we find a node which completely encloses the moved object (most of the time, the current node still encloses the object). If the object isn't completely enclosed by the current node, we keep moving it up to its next parent node. In the worst case, our root node will be guaranteed to contain the object.
After we've moved our object as far up the tree as possible, we'll try to move it as far down the tree as we can. Most of the time, if we moved the object up, we won't be able to move it back down. But, if the object moved so that a child node of the current node could contain it, we have the chance to push it back down the tree. It's important to be able to move objects down the tree as well, or else all moving objects would eventually migrate to the top and we'd start getting some performance problems during collision detection routines.
Branch Removal
In some cases, an object will move out of a node and that node will no longer have any objects contained within it, nor have any children which contain objects. If this happens, we have an empty branch and we need to mark it as such and prune this dead branch off the tree.
There is an interesting question hiding here: When do you want to prune the dead branches off a tree? Allocating new memory costs time, so if we're just going to reuse this same region in a few cycles, why not keep it around for a bit? How long can we keep it around before it becomes more expensive to maintain the dead branch? I decided to give each of my nodes a countdown timer which activates when the branch is dead. If an object moves into this nodes octant while the death timer is active, I double the lifespan and reset the death timer. This ensures that octants which are frequently used are hot and stick around, and nodes which are infrequently used are removed before they start to cost more than they're worth.
A practical example of this usefulness would be apparent when you have a machine gun shooting a stream of bullets. Those bullets follow in close succession of each other, so it'd be a shame to immediately delete a node as soon as the first bullet leaves it, only to recreate it a fraction of a second later as the second bullet re-enters it. And if there's a lot of bullets, we can probably keep these octants around for a little while. If a child branch is empty and hasn't been used in a while, it's safe to prune it out of our tree.
Anyways, let's look at the code which does all of this magic. First up, we have the Update() method. This is a method which is recursively called on all child trees. It moves all objects around, does some housekeeping work for the data structure, and then moves each moved object into its correct node (parent or child).
public void Update(coreTime time)
{
if (m_treeBuilt == true && m_treeReady == true)
{
//Start a count down death timer for any leaf nodes which don't have objects or children.
//when the timer reaches zero, we delete the leaf. If the node is reused before death, we double its lifespan.
//this gives us a "frequency" usage score and lets us avoid allocating and deallocating memory unnecessarily
if (m_objects.Count == 0)
{
if (HasChildren == false)
{
if (m_curLife == -1)
m_curLife = m_maxLifespan;
else if (m_curLife > 0)
{
m_curLife--;
}
}
}
else
{
if (m_curLife != -1)
{
if (m_maxLifespan <= 64)
m_maxLifespan *= 2;
m_curLife = -1;
}
}
List<Physical> movedObjects = new List<Physical>(m_objects.Count);
//go through and update every object in the current tree node
foreach (Physical gameObj in m_objects)
{
//we should figure out if an object actually moved so that we know whether we need to update this node in the tree.
if (gameObj.Update(time) == 1)
{
movedObjects.Add(gameObj);
}
}
//prune any dead objects from the tree.
int listSize = m_objects.Count;
for (int a = 0; a < listSize; a++)
{
if (!m_objects[a].Alive)
{
if (movedObjects.Contains(m_objects[a]))
movedObjects.Remove(m_objects[a]);
m_objects.RemoveAt(a--);
listSize--;
}
}
//prune out any dead branches in the tree
for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++)
if ((flags & 1) == 1 && m_childNode[index].m_curLife == 0)
{
if (m_childNode[index].m_objects.Count > 0)
{
//throw new Exception("Tried to delete a used branch!");
m_childNode[index].m_curLife = -1;
}
else
{
m_childNode[index] = null;
m_activeNodes ^= (byte)(1 << index); //remove the node from the active nodes flag list
}
}
//recursively update any child nodes.
for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++)
{
if ((flags & 1) == 1)
{
if(m_childNode!=null && m_childNode[index] != null)
m_childNode[index].Update(time);
}
}
//If an object moved, we can insert it into the parent and that will insert it into the correct tree node.
//note that we have to do this last so that we don't accidentally update the same object more than once per frame.
foreach (Physical movedObj in movedObjects)
{
OctTree current = this;
//figure out how far up the tree we need to go to reinsert our moved object
//we are either using a bounding rect or a bounding sphere
//try to move the object into an enclosing parent node until we've got full containment
if (movedObj.EnclosingBox.Max != movedObj.EnclosingBox.Min)
{
while (current.m_region.Contains(movedObj.EnclosingBox) != ContainmentType.Contains)
if (current._parent != null) current = current._parent;
else
{
break; //prevent infinite loops when we go out of bounds of the root node region
}
}
else
{
ContainmentType ct = current.m_region.Contains(movedObj.EnclosingSphere);
while (ct != ContainmentType.Contains)//we must be using a bounding sphere, so check for its containment.
{
if (current._parent != null)
{
current = current._parent;
}
else
{
//the root region cannot contain the object, so we need to completely rebuild the whole tree.
//The rarity of this event is rare enough where we can afford to take all objects out of the existing tree and rebuild the entire thing.
List<Physical> tmp = m_root.AllObjects();
m_root.UnloadContent();
Enqueue(tmp);//add to pending queue
return;
}
ct = current.m_region.Contains(movedObj.EnclosingSphere);
}
}
//now, remove the object from the current node and insert it into the current containing node.
m_objects.Remove(movedObj);
current.Insert(movedObj); //this will try to insert the object as deep into the tree as we can go.
}
//now that all objects have moved and they've been placed into their correct nodes in the octree, we can look for collisions.
if (IsRoot == true)
{
//This will recursively gather up all collisions and create a list of them.
//this is simply a matter of comparing all objects in the current root node with all objects in all child nodes.
//note: we can assume that every collision will only be between objects which have moved.
//note 2: An explosion can be centered on a point but grow in size over time. In this case, you'll have to override the update method for the explosion.
List<IntersectionRecord> irList = GetIntersection(new List<Physical>());
foreach (IntersectionRecord ir in irList)
{
if (ir.PhysicalObject != null)
ir.PhysicalObject.HandleIntersection(ir);
if (ir.OtherPhysicalObject != null)
ir.OtherPhysicalObject.HandleIntersection(ir);
}
}
}//end if tree built
else
{
if (m_pendingInsertion.Count > 0)
{
ProcessPendingItems();
Update(time); //try this again...
}
}
}Note that we call an Insert() method for moved objects. The insertion of objects into the tree is very similar to the method used to build the initial tree. Insert() will try to push objects as far down the tree as possible. Notice that I also try to avoid creating new bounding areas if I can use an existing one from a child node.
/// <summary>
/// A tree has already been created, so we're going to try to insert an item into the tree without rebuilding the whole thing
/// </summary>
/// <typeparam name="T">A physical object</typeparam>
/// <param name="Item">The physical object to insert into the tree</param>
private bool Insert<T>(T Item) where T : Physical
{
/*if the current node is an empty leaf node, just insert and leave it.*/
//if (m_objects.Count == 0 && m_activeNodes == 0)
if(AllTreeObjects.Count == 0)
{
m_objects.Add(Item);
return true;
}
//Check to see if the dimensions of the box are greater than the minimum dimensions.
//If we're at the smallest size, just insert the item here. We can't go any lower!
Vector3 dimensions = m_region.Max - m_region.Min;
if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE)
{
m_objects.Add(Item);
return true;
}
//The object won't fit into the current region, so it won't fit into any child regions.
//therefore, try to push it up the tree. If we're at the root node, we need to resize the whole tree.
if (m_region.Contains(Item.EnclosingSphere) != ContainmentType.Contains)
{
if (this._parent != null)
return this._parent.Insert(Item);
else
return false;
}
//At this point, we at least know this region can contain the object but there are child nodes. Let's try to see if the object will fit
//within a subregion of this region.
Vector3 half = dimensions / 2.0f;
Vector3 center = m_region.Min + half;
//Find or create subdivided regions for each octant in the current region
BoundingBox[] childOctant = new BoundingBox[8];
childOctant[0] = (m_childNode[0] != null) ? m_childNode[0].m_region : new BoundingBox(m_region.Min, center);
childOctant[1] = (m_childNode[1] != null) ? m_childNode[1].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z));
childOctant[2] = (m_childNode[2] != null) ? m_childNode[2].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z));
childOctant[3] = (m_childNode[3] != null) ? m_childNode[3].m_region : new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z));
childOctant[4] = (m_childNode[4] != null) ? m_childNode[4].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z));
childOctant[5] = (m_childNode[5] != null) ? m_childNode[5].m_region : new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z));
childOctant[6] = (m_childNode[6] != null) ? m_childNode[6].m_region : new BoundingBox(center, m_region.Max);
childOctant[7] = (m_childNode[7] != null) ? m_childNode[7].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z));
//First, is the item completely contained within the root bounding box?
//note2: I shouldn't actually have to compensate for this. If an object is out of our predefined bounds, then we have a problem/error.
// Wrong. Our initial bounding box for the terrain is constricting its height to the highest peak. Flying units will be above that.
// Fix: I resized the enclosing box to 256x256x256. This should be sufficient.
if (Item.EnclosingBox.Max != Item.EnclosingBox.Min && m_region.Contains(Item.EnclosingBox) == ContainmentType.Contains)
{
bool found = false;
//we will try to place the object into a child node. If we can't fit it in a child node, then we insert it into the current node object list.
for(int a=0;a<8;a++)
{
//is the object fully contained within a quadrant?
if (childOctant[a].Contains(Item.EnclosingBox) == ContainmentType.Contains)
{
if (m_childNode[a] != null)
{
return m_childNode[a].Insert(Item); //Add the item into that tree and let the child tree figure out what to do with it
}
else
{
m_childNode[a] = CreateNode(childOctant[a], Item); //create a new tree node with the item
m_activeNodes |= (byte)(1 << a);
}
found = true;
}
}
//we couldn't fit the item into a smaller box, so we'll have to insert it in this region
if (!found)
{
m_objects.Add(Item);
return true;
}
}
else if (Item.EnclosingSphere.Radius != 0 && m_region.Contains(Item.EnclosingSphere) == ContainmentType.Contains)
{
bool found = false;
//we will try to place the object into a child node. If we can't fit it in a child node, then we insert it into the current node object list.
for (int a = 0; a < 8; a++)
{
//is the object contained within a child quadrant?
if (childOctant[a].Contains(Item.EnclosingSphere) == ContainmentType.Contains)
{
if (m_childNode[a] != null)
{
return m_childNode[a].Insert(Item); //Add the item into that tree and let the child tree figure out what to do with it
}
else
{
m_childNode[a] = CreateNode(childOctant[a], Item); //create a new tree node with the item
m_activeNodes |= (byte)(1 << a);
}
found = true;
}
}
//we couldn't fit the item into a smaller box, so we'll have to insert it in this region
if (!found)
{
m_objects.Add(Item);
return true;
}
}
//either the item lies outside of the enclosed bounding box or it is intersecting it. Either way, we need to rebuild
//the entire tree by enlarging the containing bounding box
return false;
}
Collision Detection
Finally, our octree has been built and everything is as it should be. How do we perform collision detection against it? First, let's list out the different ways we want to look for collisions:
- Frustum intersections. We may have a frustum which intersects with a region of the world. We only want the objects which intersect with the given frustum. This is particularly useful for culling regions outside of the camera view space, and for figuring out what objects are within a mouse selection area.
- Ray intersections. We may want to shoot a directional ray from any given point and want to know either the nearest intersecting object or get a list of all objects which intersect that ray (like a rail gun). This is very useful for mouse picking. If the user clicks on the screen, we want to draw a ray into the world and figure out what they clicked on.
- Bounding Box intersections. We want to know which objects in the world are intersecting a given bounding box. This is most useful for "box" shaped game objects (houses, cars, etc).
- Bounding Sphere Intersections. We want to know which objects are intersecting with a given bounding sphere. Most objects will probably be using a bounding sphere for coarse collision detection since the mathematics is computationally the least expensive and somewhat easy.
The main idea behind recursive collision detection processing for an octree is that you start at the root/current node and test for intersection with all objects in that node against the intersector. Then, you do a bounding box intersection test against all active child nodes with the intersector. If a child node fails this intersection test, you can completely ignore the rest of that child's tree. If a child node passes the intersection test, you recursively traverse down the tree and repeat. Each node should pass a list of intersection records up to its caller, which appends those intersections to its own list of intersections. When the recursion finishes, the original caller will get a list of every intersection for the given intersector. The beauty of this is that it takes very little code to implement and performance is very fast. In a lot of these collisions, we're probably going to be getting a lot of results. We're also going to want to have some way of responding to each collision, depending on what objects are colliding.
For example, a player hero should pick up a floating bonus item (quad damage!), but a rocket shouldn't explode if it hits said bonus item. I created a new class to contain information about each intersection. This class contains references to the intersecting objects, the point of intersection, the normal at the point of intersection, etc. These intersection records become quite useful when you pass them to an object and tell them to handle it. For completeness and clarity, here is my intersection record class:
public class IntersectionRecord
{
readonly Vector3 m_position, m_normal;
readonly Ray m_ray;
readonly Physical m_intersectedObject1, m_intersectedObject2;
readonly double m_distance;
public class Builder
{
public Vector3 Position, Normal;
public Physical Object1, Object2;
public Ray hitRay;
public double Distance;
public Builder()
{
Distance = double.MaxValue;
}
public Builder(IntersectionRecord copy)
{
Position = copy.m_position;
Normal = copy.m_normal;
Object1 = copy.m_intersectedObject1;
Object2 = copy.m_intersectedObject2;
hitRay = copy.m_ray;
Distance = copy.m_distance;
}
public IntersectionRecord Build()
{
return new IntersectionRecord(Position, Normal, Object1, Object2, hitRay, Distance);
}
}
#region Constructors
IntersectionRecord(Vector3 pos, Vector3 normal, Physical obj1, Physical obj2, Ray r, double dist)
{
m_position = pos;
m_normal = normal;
m_intersectedObject1 = obj1;
m_intersectedObject2 = obj2;
m_ray = r;
m_distance = dist;
}
#endregion
#region Accessors
/// <summary>
/// This is the exact point in 3D space which has an intersection.
/// </summary>
public Vector3 Position { get { return m_position; } }
/// <summary>
/// This is the normal of the surface at the point of intersection
/// </summary>
public Vector3 Normal { get { return m_normal; } }
/// <summary>
/// This is the ray which caused the intersection
/// </summary>
public Ray Ray { get { return m_ray; } }
/// <summary>
/// This is the object which is being intersected
/// </summary>
public Physical PhysicalObject
{
get { return m_intersectedObject1; }
}
/// <summary>
/// This is the other object being intersected (may be null, as in the case of a ray-object intersection)
/// </summary>
public Physical OtherPhysicalObject
{
get { return m_intersectedObject2; }
}
/// <summary>
/// This is the distance from the ray to the intersection point.
/// You'll usually want to use the nearest collision point if you get multiple intersections.
/// </summary>
public double Distance { get { return m_distance; } }
#endregion
#region Overrides
public override string ToString()
{
return "Hit: " + m_intersectedObject1.ToString();
}
public override int GetHashCode()
{
return base.GetHashCode();
}
/// <summary>
/// check the object identities between the two intersection records. If they match in either order, we have a duplicate.
/// </summary>
/// <param name="otherRecord">the other record to compare against</param>
/// <returns>true if the records are an intersection for the same pair of objects, false otherwise.</returns>
public override bool Equals(object otherRecord)
{
IntersectionRecord o = (IntersectionRecord)otherRecord;
//
//return (m_intersectedObject1 != null && m_intersectedObject2 != null && m_intersectedObject1.ID == m_intersectedObject2.ID);
if (otherRecord == null)
return false;
if (o.m_intersectedObject1.ID == m_intersectedObject1.ID && o.m_intersectedObject2.ID == m_intersectedObject2.ID)
return true;
if (o.m_intersectedObject1.ID == m_intersectedObject2.ID && o.m_intersectedObject2.ID == m_intersectedObject1.ID)
return true;
return false;
}
#endregion
}Intersection with a Bounding Frustum
/// <summary>
/// Gives you a list of all intersection records which intersect or are contained within the given frustum area
/// </summary>
/// <param name="frustum">The containing frustum to check for intersection/containment with</param>
/// <returns>A list of intersection records with collisions</returns>
private List<IntersectionRecord> GetIntersection(BoundingFrustum frustum, PhysicalType type = PhysicalType.ALL)
{
if (!m_treeBuilt) return new List<IntersectionRecord>();
if (m_objects.Count == 0 && HasChildren == false) //terminator for any recursion
return null;
List<IntersectionRecord> ret = new List<IntersectionRecord>();
//test each object in the list for intersection
foreach (Physical obj in m_objects)
{
//skip any objects which don't meet our type criteria
if ((int)((int)type & (int)obj.Type) == 0)
continue;
//test for intersection
IntersectionRecord ir = obj.Intersects(frustum);
if (ir != null)
ret.Add(ir);
}
//test each object in the list for intersection
for (int a = 0; a < 8; a++)
{
if (m_childNode[a] != null && (frustum.Contains(m_childNode[a].m_region) == ContainmentType.Intersects || frustum.Contains(m_childNode[a].m_region) == ContainmentType.Contains))
{
List<IntersectionRecord> hitList = m_childNode[a].GetIntersection(frustum, type);
if (hitList != null) ret.AddRange(hitList);
}
}
return ret;
}The bounding frustum intersection list can be used to only render objects which are visible to the current camera view. I use a scene database to figure out how to render all objects in the game world. Here is a snippet of code from my rendering function which uses the bounding frustum of the active camera:
///
/// This renders every active object in the scene database ///
///
public int Render()
{
int triangles = 0;
//Renders all visible objects by iterating through the oct tree recursively and testing for intersection
//with the current camera view frustum
foreach (IntersectionRecord ir in m_octTree.AllIntersections(m_cameras[m_activeCamera].Frustum))
{
ir.PhysicalObject.SetDirectionalLight(m_globalLight[0].Direction, m_globalLight[0].Color);
ir.PhysicalObject.View = m_cameras[m_activeCamera].View;
ir.PhysicalObject.Projection = m_cameras[m_activeCamera].Projection;
ir.PhysicalObject.UpdateLOD(m_cameras[m_activeCamera]);
triangles += ir.PhysicalObject.Render(m_cameras[m_activeCamera]);
}
return triangles;
} Intersection with a Ray
/// <summary>
/// Gives you a list of intersection records for all objects which intersect with the given ray
/// </summary>
/// <param name="intersectRay">The ray to intersect objects against</param>
/// <returns>A list of all intersections</returns>
private List<IntersectionRecord> GetIntersection(Ray intersectRay, PhysicalType type = PhysicalType.ALL)
{
if (!m_treeBuilt) return new List<IntersectionRecord>();
if (m_objects.Count == 0 && HasChildren == false) //terminator for any recursion
return null;
List<IntersectionRecord> ret = new List<IntersectionRecord>();
//the ray is intersecting this region, so we have to check for intersection with all of our contained objects and child regions.
//test each object in the list for intersection
foreach (Physical obj in m_objects)
{
//skip any objects which don't meet our type criteria
if ((int)((int)type & (int)obj.Type) == 0)
continue;
IntersectionRecord ir = obj.Intersects(intersectRay);
if (ir != null)
ret.Add(ir);
}
// test each child octant for intersection
for (int a = 0; a < 8; a++)
{
if (m_childNode[a] != null && m_childNode[a].m_region.Intersects(intersectRay) != null)
{
m_lineColor = Color.Red;
List<IntersectionRecord> hits = m_childNode[a].GetIntersection(intersectRay, type);
if (hits != null && hits.Count > 0)
{
ret.AddRange(hits);
}
}
}
return ret;
}Intersection with a list of objects
This is a particularly useful recursive method for determining if a list of objects in the current node intersects with any objects in any child nodes (See: Update() method for usage). It's the method which will be used most frequently, so it's good to get this right and efficient. What we want to do is start at the root node of the tree. We compare all objects in the current node against all other objects in the current node for collision. We gather up any of those collisions as intersection records and insert them into a list. We then pass our list of tested objects down to our child nodes. The child nodes will then test their objects against themselves, then against the objects we passed down to them. The child nodes will capture any collisions in a list, and return that list to its parent. The parent then takes the collision list received from its child nodes and appends it to its own list of collisions, finally returning it to its caller.
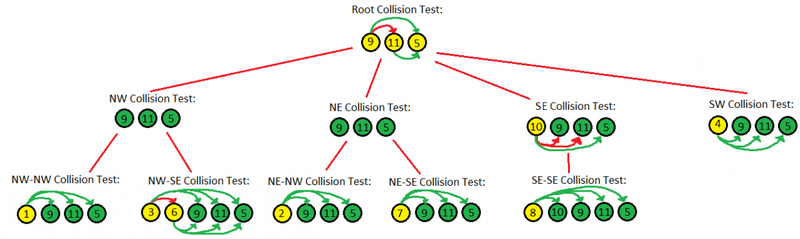
If you count out the number of collision tests in the illustration above, you can see that we conducted 29 hit tests and received 4 hits. This is much better than [11*11 = 121] hit tests.
private List<IntersectionRecord> GetIntersection(List<Physical> parentObjs, PhysicalType type = PhysicalType.ALL)
{
List<IntersectionRecord> intersections = new List<IntersectionRecord>();
//assume all parent objects have already been processed for collisions against each other.
//check all parent objects against all objects in our local node
foreach (Physical pObj in parentObjs)
{
foreach (Physical lObj in m_objects)
{
//We let the two objects check for collision against each other. They can figure out how to do the coarse and granular checks.
//all we're concerned about is whether or not a collision actually happened.
IntersectionRecord ir = pObj.Intersects(lObj);
if (ir != null)
{
//ir.m_treeNode = this;
intersections.Add(ir);
}
}
}
//now, check all our local objects against all other local objects in the node
if (m_objects != null && m_objects.Count > 1)
{
#region self-congratulation
/*
* This is a rather brilliant section of code. Normally, you'd just have two foreach loops, like so:
* foreach(Physical lObj1 in m_objects)
* {
* foreach(Physical lObj2 in m_objects)
* {
* //intersection check code
* }
* }
*
* The problem is that this runs in O(N*N) time and that we're checking for collisions with objects which have already been checked.
* Imagine you have a set of four items: {1,2,3,4}
* You'd first check: {1} vs {1,2,3,4}
* Next, you'd check {2} vs {1,2,3,4}
* but we already checked {1} vs {2}, so it's a waste to check {2} vs. {1}. What if we could skip this check by removing {1}?
* We'd have a total of 4+3+2+1 collision checks, which equates to O(N(N+1)/2) time. If N is 10, we are already doing half as many collision checks as necessary.
* Now, we can't just remove an item at the end of the 2nd for loop since that would break the iterator in the first foreach loop, so we'd have to use a
* regular for(int i=0;i<size;i++) style loop for the first loop and reduce size each iteration. This works...but look at the for loop: we're allocating memory for
* two additional variables: i and size. What if we could figure out some way to eliminate those variables?
* So, who says that we have to start from the front of a list? We can start from the back end and still get the same end results. With this in mind,
* we can completely get rid of a for loop and use a while loop which has a conditional on the capacity of a temporary list being greater than 0.
* since we can poll the list capacity for free, we can use the capacity as an indexer into the list items. Now we don't have to increment an indexer either!
* The result is below.
*/
#endregion
List<Physical> tmp = new List<Physical>(m_objects.Count);
tmp.AddRange(m_objects);
while (tmp.Count > 0)
{
foreach (Physical lObj2 in tmp)
{
if (tmp[tmp.Count - 1] == lObj2 || (tmp[tmp.Count - 1].IsStationary && lObj2.IsStationary))
continue;
IntersectionRecord ir = tmp[tmp.Count - 1].Intersects(lObj2);
if (ir != null)
{
//ir.m_treeNode = this;
intersections.Add(ir);
}
}
//remove this object from the temp list so that we can run in O(N(N+1)/2) time instead of O(N*N)
tmp.RemoveAt(tmp.Count-1);
}
}
//now, merge our local objects list with the parent objects list, then pass it down to all children.
foreach (Physical lObj in m_objects)
if (lObj.IsStationary == false)
parentObjs.Add(lObj);
//parentObjs.AddRange(m_objects);
//each child node will give us a list of intersection records, which we then merge with our own intersection records.
for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++)
{
if ((flags & 1) == 1)
{
if(m_childNode != null && m_childNode[index] != null)
intersections.AddRange(m_childNode[index].GetIntersection(parentObjs, type));
}
}
return intersections;
}Screenshot Demos
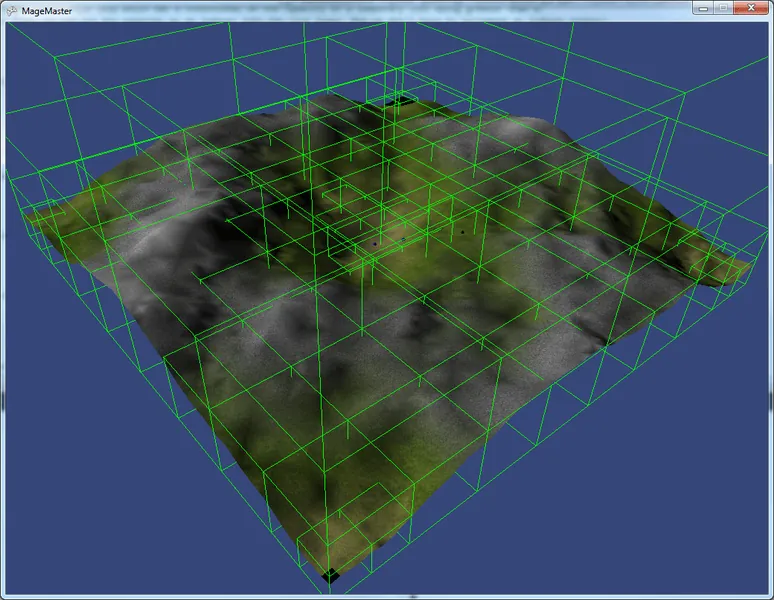 This is a view of the game world from a distance showing the outlines for each bounding volume for the octree.
This is a view of the game world from a distance showing the outlines for each bounding volume for the octree. 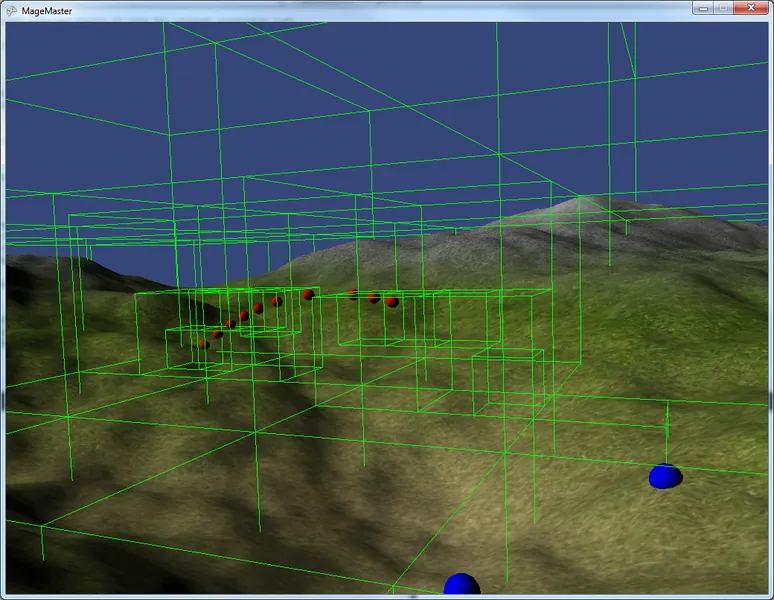 This view shows a bunch of successive projectiles moving through the game world with the frequently-used nodes being preserved instead of deleted.
This view shows a bunch of successive projectiles moving through the game world with the frequently-used nodes being preserved instead of deleted.
Complete Code Sample
I've attached a complete code sample of the octree class, the intersection record class, and my generic physical object class. I don't guarantee that they're all bug-free since it's all a work in progress and hasn't been rigorously tested yet.









Im not a fan of quadtree or octree, but must admit that article its one of the best...