Hi, hopefully I've got the right forum for this question. I'm more of a DSP maths person, so 3D maths isn't something I'm all that familiar with. Please bear with me if I'm missing obvious things.
I'm working on a project that uses a pre-rendered background of a 3D space, combined with a 3D mesh that a player can move on. The implementation of the walkmesh I'm using is very simple, as I don't need anything complicated, and works exclusively on the xz plane (z = forward/back), with the final y position just being calculated once movement has finished. I can't just use an off-the-shelf library, because this is running on a very limited platform, on which I don't think I've seen any open-source tools for this (Nintendo GBA).
Implementation notes:
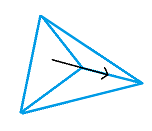
- Every entity gets assigned to a triangle in the walk mesh when spawned.
- To traverse the mesh, I take in the entity's current world position + associated triangle, and a walk vector (eg. {0,0,1} = Move 1.0 units along the triangle's yz plane).
Implementation steps:
- Project the move vector onto the triangle's plane (ie. vDisplace = vWalk - (vWalk.TriNormal)*TriNormal) and displace the current entity position by vDisplace. This is to make it appear as though the entity is traversing that distance on the mesh rather than just the world axes.
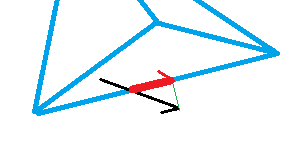
- Do a simple edge test against all sides of the current triangle to se if the new position lies outside the current triangle.
- If the new position is inside the triangle, then everything's fine; exit by going to step 7.
- If the new position is outside the triangle, then use the result of the edge tests to clip to the triangle's edges (eg. if the point is outside v1v2, clip against v1v2, and so on for v2v3 and v3v1).
- Subtract the movement to the clipped position from the original intended movement (vWalk *= 1.0 - Length(vNewPos-vOldPos)/Length(vWalk)).
- Use the edge tests combined with the triangle's edge connectivity to determine a new triangle to traverse to (eg. if v1v2 was crossed and a triangle exists across it, then select that). If a triangle exists, then restart at step 1 using that triangle and the current position + walk vectors.
- Either we hit a dead-end edge, or the entity is inside the current triangle (came here from step 4). Either way, store the current y position and finish.
While this seems to be working fine, there's two things I want to add:
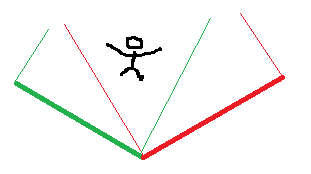
- Say an entity is moving by vWalk={0.7,0,0.7}, but is colliding with a wall on the x axis. Using the current system, the entity just gets "stuck" because it collides with a wall in the current direction and gets clipped. I would like to see instead a 'slide' against a wall. I've tried setting vWalk = vEdge * Length(vWalk)/Length(vEdge), but this seems to glitch out (probably from some precision issues, to be honest; all the maths needs to be done using fixed-point integers), and there's issues regarding which direction I'm moving in relative to the edge direction, anyway (ie. whether I used v1-v2 or v2-v1).
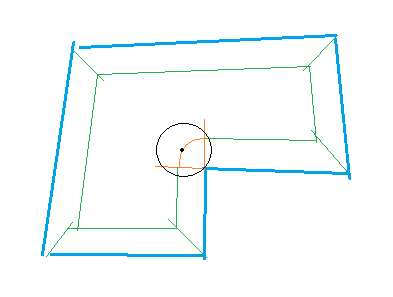
- While point collisions are a good place to start, ideally I'd have a sphere collision against edges (or rather, a circle collision, since I'm only actually referencing the xz planes). I really have no idea where to start on this, though.
A major point about the implementation is that it can't just use wild expressions everywhere, due to lack of CPU resources (eg. dot products are great, cross products are ok, but square roots and divisions should be as rare as possible; it's to the point where I'm calculating Sqrt[a/b] as 1/Sqrt[b/a] because I have fast routines for approximate reciprocals and approximate inverse square roots, which are faster than calculating divisions and square roots directly).
Does anyone know of any resources I could read up on to help with what I'm trying to do? From the looks of things, walkmesh implementations are mostly a thing of the past, with basically everything now just using physics engines directly, so I've been having a really hard time finding anything, and built my current implementation mostly based on intuition, with occasional maths-related searches.