P.P.S. I need a number library that lets you specify the number of exponent bits and mantissa bits. Ttmath uses 64-bits for each by default when compiling for x64.

Aha. It looks like Boost::Multiprecision lets you specify the number of bits.

In fwd.hpp:

    using cpp_complex_single = cpp_complex<24, backends::digit_base_2, void, std::int16_t, -126, 127>;
    using cpp_complex_double = cpp_complex<53, backends::digit_base_2, void, std::int16_t, -1022, 1023>;
    using cpp_complex_extended = cpp_complex<64, backends::digit_base_2, void, std::int16_t, -16382, 16383>;
    using cpp_complex_quad = cpp_complex<113, backends::digit_base_2, void, std::int16_t, -16382, 16383>;
    using cpp_complex_oct = cpp_complex<237, backends::digit_base_2, void, std::int32_t, -262142, 262143>;

so what kind of number should we use next? I mean, we know that for the single precision float that it works the way we want it. Should we try something like 30 mantissa bits?

taby said:
The effect here is grossly exaggerated.

Ah ok. I was already assuming that the ellipse trajectory is rotating over time, so you get an angle.
But with the current setup, even after dozens of orbits the effect isn't noticeable?
You need data for Planet 9, or some other solar system with more action going on.

taby said:
It's a very tiny amount, yes, but at the macroscopic scale it all turns out to be pretty much exactly what is observed (47 versus 43 arcseconds per Earth century).

That's more than a view dozens, i see.
But still i do not accept it as confirmation that reducing precision could be in a physics equation.
No, no, and no. It's just random coincidence. God does not use a buggy Pentium.

But well, that's just me. Ignore it, and keep hunting the precision ghost. ; )

taby said:
Note that 43 arcseconds is like 0.0002 radian… a macrosliver… made up of even tinier microslivers (that is, 88 Earth days / 0.01 seconds = 760320000 microslivers in total). For all of the values possible, it just happens to luck out? No, it's a systemic property, I used google to do these arithmetic. :)

With values so tiny, i doubt scientists can be sure their given numbers are precise at all. How could they know Mercurys mass and trajectory so exactly?
Instead messing with precision, you should tweak those initial parameters to get the correct result, if at all.
And even then, adding the other planets would again change everything i guess.

taby said:
Note that the symplectic and Euler integration give roughly the same amount. Using Euler is not a weakness – it serves as a reference.

But reducing precision does not serve as reference.

I would just stick at double precision and trust in that.

JoeJ said:
God does not use a buggy Pentium.

Um, maybe the Simulation Theory is right? And they thought float is good enough to handle gravity?

Then you could be right. :D

There's no possible way you are getting a more accurate result with single precision than double precision, as doubles are inherently a superset of single precision and will always be at least as accurate. Any better “accuracy” with single precision is just a coincidence. You should be able to use doubles or even higher precision and in the limit of infinite precision your calculations will be mathematically exact. If you aren't getting the expected result with a high precision number type then you have other sources of error (e.g. in the algorithm itself). Throwing more (or less) bits at it won't help in that case.

I'll repost Frob's link from the second page: What Every Computer Scientist Should Know About Floating Point.

Most of this thread is just nonsense.

Aressera said:

There's no possible way you are getting a more accurate result with single precision than double precision,

You imply that the answer is strictly monotonically decreasing, based on the numher of bits. What will you say when it doesn't turn out to be that way?

Thanks for your input yet again, JoeJ!

I have added measurement of angles using complex numbers, which should be better than acos.
But seems to confirm your former results:

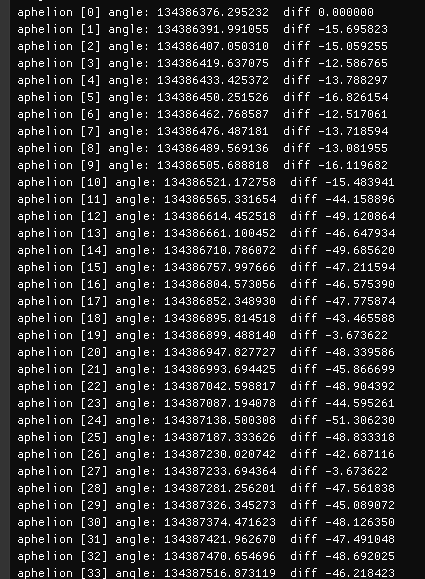
Orbits 0-10 use doubles, the rest uses cast to float.

Modifications on the code:

static std::vector<vector_3> aphelions;
...
if (mercury_pos.length() < last_pos.length())
					{
						// hit aphelion
						SystemTools::Log("[%i] hit aphelion\n", frame_count);

						aphelions.push_back(mercury_pos);

						orbit_count++;
...
std::complex<double> prev_aph; 
				for (size_t i=0; i<aphelions.size(); i++)
				{
					std::complex<double> aph (aphelions[i].x, aphelions[i].y);
					double angle = std::arg(aph);
					double angleDiff = 0;
					if (i > 0) angleDiff = std::arg(prev_aph / aph);
					prev_aph = aph;

					vec a (aphelions[i].x*scale, aphelions[i].y*scale, aphelions[i].z*scale);
					float t = float(i) / float(aphelions.size()) * 0.66f;
					RenderPoint (a, RainbowR(t), RainbowG(t), RainbowB(t)); 

					ImGui::Text("aphelion [%i] angle: %f  diff %f", i, 
						angle * num_orbits_per_earth_century * to_arcseconds, 
						angleDiff * num_orbits_per_earth_century * to_arcseconds);
				}

Finally some results using the bit mask:

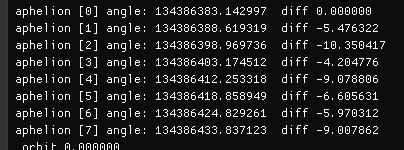
Problem with the measurement is that i still measure difference between steps, so very small angles.
Taking angles to a global reference and using that might be better, assuming trig functions have problems with tiny angles.

But looking at the current numbers i have little hope this would bring some enlightenment.

The casting mystery remains upright. : /

taby said:
You imply that the answer is strictly monotonically decreasing, based on the numher of bits. What will you say when it doesn't turn out to be that way?

I'll say that it's a fluke and a coincidence, which it will be. Doubles have more precision than floats. There's no possible way for floats to be any more accurate. Any value that can be represented in floats can be exactly represented in doubles. This is by design. If you used 128-bit floats, they would be more accurate than doubles. Adding more exponent/mantissa bits adds more precision because it allows representation of values with finer resolution.

An analogy to your argument is that because sometimes integer calculations can produce the same value as floats (1+2 == 3 == 1.0f + 2.0f), that integers are more accurate in the general case. This is nonsensical. “float” is a better representation of real numbers than “int”, and “double” is better than “float”. “long double” can be better than “double”, depending on the platform and implementation.

As I stated at least twice, if you aren't getting the expected result with a complex calculation in double precision, it's far more likely to be the result of an imperfect algorithm (e.g. how you time step the simulation), than it is to be the result of numerical precision, unless you are doing something dumb like adding a tiny number to a big number. In any case, numerical error should vanish to 0 as you add more precision. This is the whole reason why high precision libraries exist, so that calculations with huge range of values can be implemented with more accuracy.