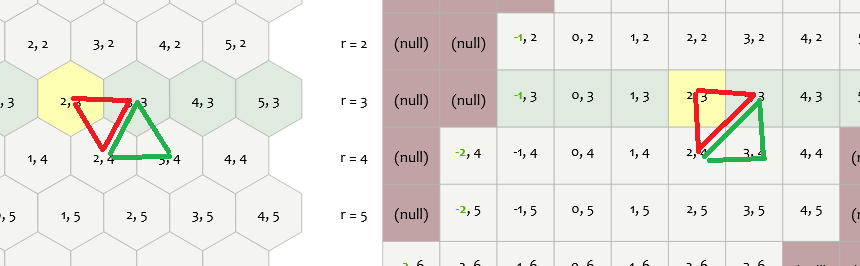
I have a pointy topped hex grid based on cube coordinates, created by following this great guide from Red Blob Games: https://www.redblobgames.com/grids/hexagons/.
I know that the dual graph of a hex grid, a triangle grid, can be formed by treating the center of each hexagon as a vertex of a triangle. I want to use this fact to draw a terrain on the triangular grid, based on the hex grid, as explained in this fantastic talk by Oskar Stålberg (at 7:00):
However, I'm struggling with how to “access” the dual grid. More specifically, how can I iterate over every triangle in the dual grid and also get the 3 hexagons it is formed by, without visiting the same triangles multiple times?
Do I create and store the two grids as separate data structures in code, or do I derive the dual grid from the hex grid?
A naive way would be to iterate over all hexagon, and get each hexagon's 6 cartesian corner coordinates, which is also the center position of each triangle face. Then based on the face position find the cube coordinates of the 3 closest hexagons. But that means it will visit every triangle 3 times, which seems unnecessary.