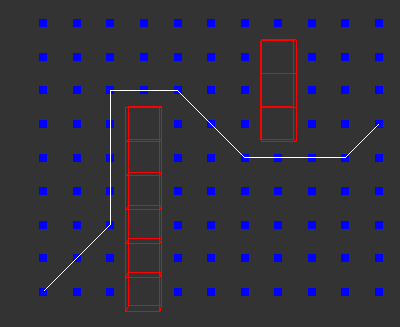
I wrote some basic A* code without any effort to optimize performance. It should be fairly easy to read.
In the worst case (when the goal is surrounded by obstacles and there is no path, but the algorithm needs to explore the entire map to conclude that) it takes about 6-9 milliseconds on my [fast] computer for a 256x256 map. Easy cases take about 0.6 milliseconds. This is quite a bit worse than I was hoping for. For an old computer this would be intolerable. If I have a bit of time I might try to optimize the code, for my own entertainment. I can think of at least one large performance improvement available, but it's not straight forward to implement.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <chrono>
struct Map {
int height, width;
std::vector<int> data;
Map(int height, int width, int initial_value) : height(height), width(width), data(height * width, initial_value) {
}
Map(int height, int width) : height(height), width(width), data(height * width) {
}
int &operator[](int x) {
return data[x];
}
int operator[] (int x) const {
return data[x];
}
int &operator()(int x, int y) {
return data[y * width + x];
}
int operator() (int x, int y) const {
return data[y * width + x];
}
};
int heuristic_cost(int a_x, int a_y, int b_x, int b_y) {
int delta_x = std::abs(a_x - b_x);
int delta_y = std::abs(a_y - b_y);
int minimum = std::min(delta_x, delta_y);
int maximum = std::max(delta_x, delta_y);
return 10 * maximum + 4 * minimum;
}
std::vector<int> reconstructed_path(Map const &came_from, int node) {
std::vector<int> result;
while (1) {
result.push_back(node);
int previous = came_from[node];
if (previous == node)
break;
node = previous;
}
std::reverse(result.begin(), result.end());
return result;
}
std::vector<int> a_star(Map const &obstacles, int start_x, int start_y, int goal_x, int goal_y) {
int height = obstacles.height;
int width = obstacles.width;
int start = width * start_y + start_x;
int goal = width * goal_y + goal_x;
// Initialize distance to every node to infinity except for the start
Map distance_to_start(height, width, 1000000000);
distance_to_start[start] = 0;
Map came_from(height, width);
came_from[start] = start;
// In the open list, we use the lowest 32 bits for the position and the highest 32 bits for the cost, so the order works out
std::priority_queue<long long, std::vector<long long>, std::greater<long long>> open_list;
// Initialize open list to contain only the starting node
open_list.push(start);
while (!open_list.empty()) {
int node = open_list.top() & 0x7fffffffll;
int node_x = node % width;
int node_y = node / width;
open_list.pop();
if (distance_to_start[node] < 0) // Ignore closed nodes
continue;
if (node == goal)
return reconstructed_path(came_from, goal);
// Loop over the neighbors
for (int y_neighbor = std::max(0, node_y - 1), y_neighbor_last = std::min(height - 1, node_y + 1); y_neighbor <= y_neighbor_last; ++y_neighbor) {
for (int x_neighbor = std::max(0, node_x - 1), x_neighbor_last = std::min(width - 1, node_x + 1); x_neighbor <= x_neighbor_last; ++x_neighbor) {
if (y_neighbor == 0 && x_neighbor == 0)
continue;
if (obstacles(x_neighbor, y_neighbor) != 0 || obstacles(node_x, y_neighbor) != 0 || obstacles(x_neighbor, node_y) != 0)
continue;
int next = width * y_neighbor + x_neighbor;
int cost = heuristic_cost(node_x, node_y, x_neighbor, y_neighbor);
if (distance_to_start[next] > distance_to_start[node] + cost) {
distance_to_start[next] = distance_to_start[node] + cost;
came_from[next] = node;
open_list.push((distance_to_start[next] + heuristic_cost(x_neighbor, y_neighbor, goal_x, goal_y)) * 0x100000000ll + next);
}
}
}
distance_to_start[node] = -1; // Mark node as closed
}
return std::vector<int>(); // Failed to find path
}
int main() {
Map obstacles(256, 256);
obstacles(3, 0) = 1;
obstacles(3, 1) = 1;
obstacles(3, 2) = 1;
obstacles(3, 3) = 1;
obstacles(3, 4) = 1;
obstacles(3, 5) = 1;
obstacles(7, 5) = 1;
obstacles(7, 6) = 1;
obstacles(7, 7) = 1;
auto begin_time = std::chrono::system_clock::now();
std::vector<int> path = a_star(obstacles, 0, 0, 10, 5);
auto end_time = std::chrono::system_clock::now();
for (int x : path)
std::cout << '(' << (x%256) << ',' << x/256 << ')' << '\n';
std::cout << "Computation took " << std::chrono::duration_cast<std::chrono::microseconds>(end_time-begin_time).count() << " microseconds" << std::endl;
}