hi,
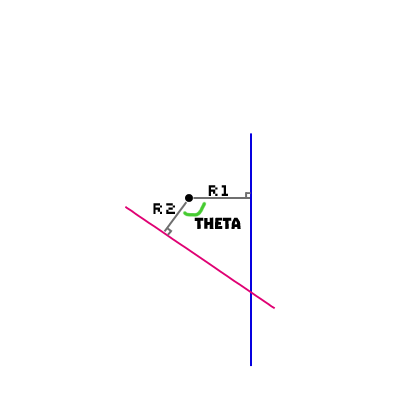
Apologies for the crude diagram; I'm trying to find the point where two lines intersect. I know how to solve this in general, given the line geometry (eg 2 points on either line), but I'd like to avoid having to convert the problem to Cartesian coordinates and back.
Currently I'm working with halfspaces described as: normal direction (in radians) and offset (distance from the origin to a point on the line, moving along the normal).
ie I'd like a function where I plug in the delta angle between normals (will never be >180deg, theta in the diagram) and the two offsets (r1 and r2 in the diagram) and get the intersection point.
Ideally this shouldn't use any transcendental functions, however I suspect a single cos() or sin() is going to be needed.
I don't need the results as cartesian coordinates, for example it might be more natural to express the intersection point as a direction to move along the tangent of the first plane (ie as theta increases from 0 to 180deg, the solution distance would increase from 0 to infinity; when theta is 90deg, the solution would be r2).
I'd like to find a solution which uses this data directly rather than converting the lines to some other form to solve the problem. If needed, I could use unit normal direction instead of angle, so that the halfspaces are described in the more natural “ABC" format.
Please let me know if I'm confused about something, or if this doesn't make sense. I don't want to work directly with vectors since I have convex shapes described as a sorted-by-angle ordered list of [angle,offset] halfspaces.