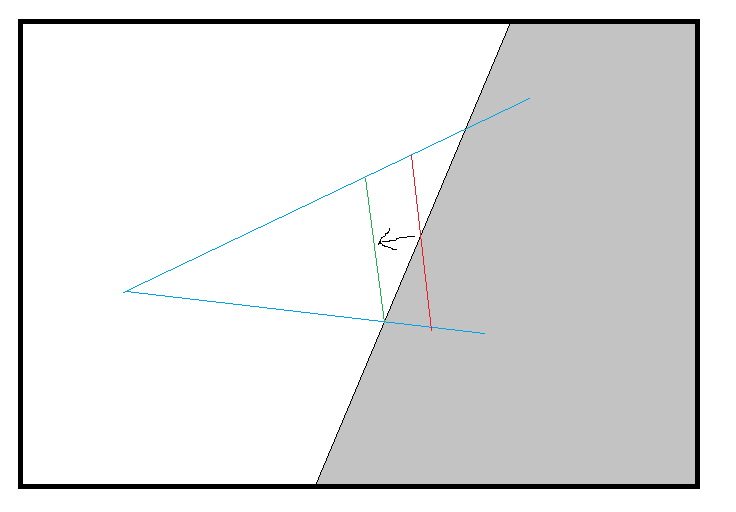
I'd like to come up with a precise formula for shadow map biases. It should be possible to do based on the resolution of the shadow map, area over which it is distributed, and surface normal. The only thing I have a problem with is the non-linear depth value. I don't know how much bias is required to ensure the next discrete value is used.

How can I calculate the discrete values that will be stored in the depth buffer, and then round off to the next lowest?

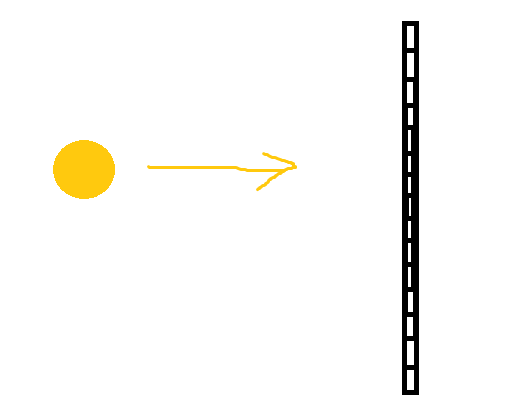
You can see here, as the surface gets closer to the light source, the depth precision increases and acne starts appearing:

There must be an equation that gives us the precise bias value needed to counteract this.

Josh Klint said:
How can I calculate the discrete values that will be stored in the depth buffer, and then round off to the next lowest?

I just tried this and it seems to work:

			float value = 0.7f;
			int32_t casted = *((int32_t*)&value);
			casted--;
			float smallerValue = *((float*)&casted);
			SystemTools::Log("value: %.16f  smaller value: %.16f  proof: %.16f\n", 
				value, smallerValue, std::nextafter(value, value-1.f));

output:

value: 0.6999999880790710 smaller value: 0.6999999284744263 proof: 0.6999999284744263

Or you could lookup the implementation of std::nextafter. Maybe there are some further caveats beyond my basic idea.

I use such integer casting on GPU to find a smallest float using atomicMin, because standard atomic ops do not support floating point numbers. This works.
But i don't know if depth buffer is backed by floats or integers, and how this depends on things like using stencil buffer as well or not.
However, iirc many years back somebody who knows said all recent modern GPUs use 32 bit floats for Z internally.

BTW, i remember a paper. They assumed flat surfaces and used the normal to intersect a patch of surface with the frustum of the shadow map texel. Then they reduced the depth value (from the center of the frustum) to the closest point of intersection.
This resolved artifacts for their example low poly scenes. Math was just two lines maybe, did not really model an accurate frustum. I can draw in image:

Blue is the texel frustum, and they pulled the red line to the green line.
I guess that's similar to what you try to do.

Promising i think - let us know how it works out : )

Josh Klint said:
There must be an equation that gives us the precise bias value needed to counteract this.

Nah, sadly not. They would have found it already. :D
I think the above idea is all we can do, but it builds on the assumption each texel covers just one flat surface patch.
If SM resolution is small and geometric detail is high this won't hold true. There might be bumps and valleys in the signal, first showing near edges.
But in practice it should work quite well i guess.

It's not just a rounding issue with discretizing the depth value that's stored in the depth/shadow map. You also get issues because there is not a 1:1 mapping between screen pixels and shadow map texels due to projective aliasing, and so the surface point that you're shading in your pixel shader will generally not be the same point that was rasterized in the shadow map. To handle this you need to determine the projected footprint of the shadow map texel(s) that you're sampling, and determine the closest point on your shading surface to the shadow casting light source (since anything but the closest point might have a greater depth, and this end up with false self-shadowing). One way to do this is to assume the shading surface is planar, and reconstruct the plane using pixel shader quad derivatives. This provides you with a fairly conservative (although not perfect) bias value, however the planar assumption means that the bias value grows quite large as your PCF kernel grows larger. Using pixel shader derivatives is also prone to discontinuities and precision issues. GPUs actually have a hardware feature that uses similar rationale to actually pre-bias the depth map itself, called slope-scaled depth bias. This uses the slope of the triangle with respect to the shadow caster to increase the bias for surfaces whose normal faces away from the light source, which is the same basic principle being applied for the quad derivative approach applied to the shading surface. Normal offset shadows are another simple approach that push the receiver position out based on the dot product between the surface normal and the shadow caster, which can give a smoother result since shading normals usually have less discontinuities.

I would recommend checking out this paper, which has a good overview of the subject and its own particular solution to the problem.

JoeJ said:
However, iirc many years back somebody who knows said all recent modern GPUs use 32 bit floats for Z internally.

They will store the depth buffer according to whatever format you used for creating the texture. In many cases the texture can consume more storage space than what's implied by the format (for instance, by storing 24-bit depth in a 32-bit texel and storing stencil separately) but that won't change the actual precision of the stored depth values.

@MJP Have you by any chance used a receiver plane depth bias in production code and worked around the discontinuity artifacting somehow?

I wonder if it would be any improvement (i.e. not introducing significant other artifacts) to use quad swaps and use the smallest receiver plane bias within a quad (or maybe separated vertically/horizontally) if the derivatives reach a certain threshold (fixed, or somehow adaptive threshold?).

@agleed I have no not. The last 4 games I shipped all used either EVSM or MSM. I think if I were to try though I would probably try to do something based on the vertex normal instead since that would avoid most of the discontinuity issues.

Variance shadow maps are the only thing I have found that can potentially solve this issue without a big performance compromise. Otherwise, I can only expose a linear and multiplicative offset per-shadow that has to be adjusted by the end user. I have not found any reliable formula that does what I want. Kind of strange that a linear depth buffer hasn't been implemented on hardware.

Linear depth doesn't isn't straightforward to interpolate. It also doesn't compress well: most desktop GPUs will take advantage of the fact that the gradients of z are constant over a triangle in order to reduce bandwidth.