Guess the links don't work, forum editor got stuck once more. But easy to find. However, i also found his implementation for some DCC plug in, and as mentioned in paper they do some taylor series stuff to approximate form factor, although they also store surfel data from which we can get this precisely without storing extra coefficients and processing them. So my method is simpler and faster.

If you only need one point, given code is likely fast enough, but if you need many points like for solid voxelization, this is how to speed it up:

1. Make acceleration structure for mesh triangles (I use simple BVH, but octree etc. would work as well)
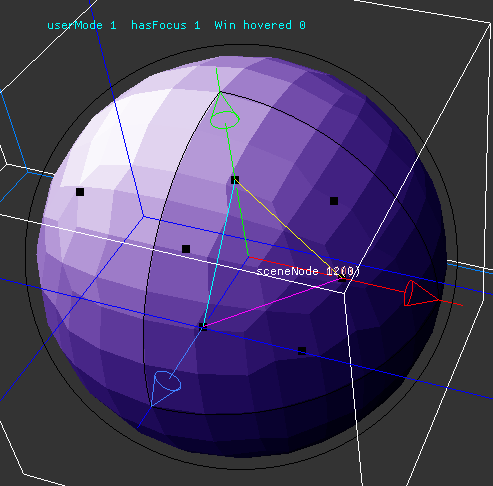
2. Calculate surfel for each triangle (using triangle area and normal)
3. Make a hierarchy bottom up: So each internal node becomes a surfel as well by summing up area and averaging normal from the surfels of all child nodes. (Exactly like here: https://developer.nvidia.com/gpugems/gpugems3/part-ii-light-and-shadows/chapter-12-high-quality-ambient-occlusion)​​​ EDIT - no, meant this earlier one: https://developer.nvidia.com/gpugems/gpugems2/part-ii-shading-lighting-and-shadows/chapter-14-dynamic-ambient-occlusion-and​
4. Finally, when traversing the surface for the query point, for distant surface patches it is good enough to stop at some internal node, also like proposed in Bunnels article above, to get O(log n). Axact triangle test is only necessary if very close to it - otherwise surfels are fine. If geometry resolution is high and uniform (like marching cubes output), exact triangle test might not be necessary at all.

Notice the speedup vs. RT approach, where you need to traverse BVH for each of maybe hundrets of rays. Surface integration is also more robust to issues like holes and imperfections, degenerate cases, non manifolds, etc.

To make it even faster, traversal stack can be shared across a query volume of points using hierarchical top down processing if we have that (not just a single point). But that's complicated so i'd do this only if you really have to. My final performance is voxelizing 20 models at 2k^3 resolution in 30 minutes IIRC.
Ofc. rasterizing + depth peeling would be much faster still, but this only works for proper manifold input (rarely the case for game models, but usually is for extracted iso surface).

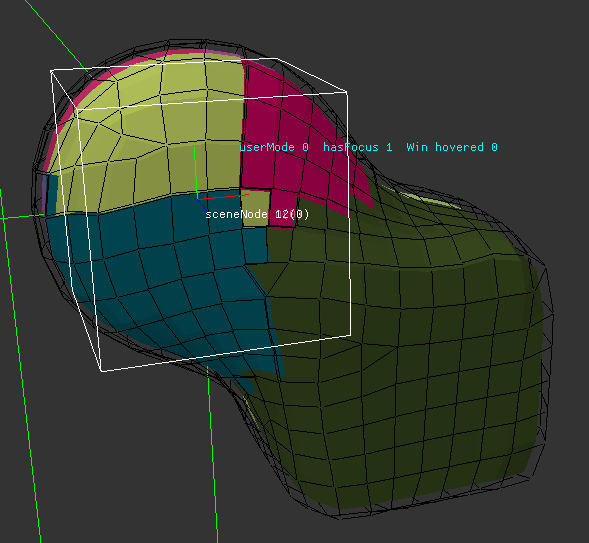
Limitations: You must know the surface normal for your input surface. If the surface points inwards or outwards.
Unfortunately this is not always given in practice. Imagine an architecture model like Sponza. The artist models a flat floor, then puts uncapped cylinders on top to get columns. Now imagine to go inside the column. You see back faces from the column which is fine, but you also see front facing floor triangles when looking down. So you do not really know if you are inside or outside. In such cases i get bulbs of empty space inside the columns near the floor. I filter them out with some heuristics, but do not remember precisely how.
This problem would appear also with RT or the winding number approach.

I was having a blond moment… Any location where the quaternion magnitude is less than 4.0 is inside the mesh. No mesh required really. Thanks for the help though guys!

taby said:
I was having a blond moment… Any location where the quaternion magnitude is less than 4.0 is inside the mesh.

: ) hihi! I was wondering what you would need this for.

btw, distance for fractals seems not that difficult. Will give it a try soon… http://www.fractalforums.com/3d-fractal-generation/a-mandelbox-distance-estimate-formula/

Pardon my ignorance, but how does distance work? Is it just for ray-tracing?

Also, it is found that any trajectory that escapes never lands within the isosurface. So it's like a black hole, with an event horizon, in a way.

Pardon my ignorance, but how does distance work? Is it just for ray-tracing?

No, i use it also for iso surface extraction, and most interestingly for geometry blending.

For example, meshing the SDF function of a sphere is quite accurate even at low res (using gizmo circle as proof):

I use the distance value to estimate density per voxel. Isosurface extraction works like minecraft mesh, then calculating density gradient and projecting vertices to resulting surface. (IDK how marching cubes does this, but probably somewhat similar working on edges.)

Distance based blending enables effects like this, adding a cube:

Pretty much like metaballs, but i can do this also with meshes. Works the same we we know from demoscene works, Inigo Quilez has it all on his webpage.

Also CSG modeling is easy once working with volumes instead surface representations.

Though, Isosurface extraction gives bad quality because aligned to worldspace grid instead local curvature. Thus i remesh it to a quaddominant mesh: 

Looks similar in this case because the models were aligned to worldspace already before, but makes big difference if they were rotated.

My initial reason to work on this is to generate good probe locations for realtime GI, but now having it i'll explore how useful this is for procedural generation. Actually working on Terrain simulations, later maybe some procedural architecture. Still need to solve texturing, rendering and compression…

Also, it is found that any trajectory that escapes never lands within the isosurface. So it's like a black hole, with an event horizon, in a way.

Not surprising to me. My own work on farctals was (as usual) to find a 3D mandelbrot.

If you plot the complex numbers for a single pixel and its iterations, at some points you get those typical spirals:

With the escape distance of 2 (iirc) shown as white circle. That's the event horizon as you say, i guess.

We talked about that, and some time later i had the idea to use spherical coordinates to project that on a sphere. It worked, and i got more interesting shapes than spirals:

(left side shows projection on a sphere)

Looks cool, but the resulting images were just the usual stretched bullshit everybody gets if messing with mandelbrot.

Then i've leraned the Mandelbulb also uses the idea of spherical coords, just slightly different. In the best case, i was close to reinventing a wheel.

So i had some fun, but i give up on it. We'll never ever find a real 3D fractal, or will we? :D
 

To be honest, I’ve never looked into Mandelbulb. I think that you’re right that there are no so-called 3D fractals, unlike the 2D, 4D, and 8D brethren.

P.S. So the isovalue is 0.0?

4D, and 8D brethren.

You mean Quaternion / Octonion based fractals? Problem is they can not compete 2D Mandelbrot either. If they would, slicing them to 3D would give us what we expect.

I'm optimistic we'll see more awesome fractals in the future, and what we have now is pretty great too. But it's not artist friendly, and any trial to change this gives a contradiction with the ideal of it being pure and elegant math. I can surely use Mandelbox to get some low efford high detail for some SciFi content, or even procedural cities. But it's no longer a fractal then. A solution could be to parametrize fractals, so we can grow then on manually designed shapes, maybe.

Maybe we just scratching on the surface of something hidden on wonderful, maybe fractals are just useless. Who knows :D

I must admit that I’ve never tried to make a quaternion Mandelbrot set, but what about the quaternion Julia sets for Z = Z^2 + C or like Z = sin(Z) + C sin(Z)? ? The quaternion fractals are so much cooler to look at than their 2D counterparts.

P.S. I found my standard quaternion Julia set code: https://github.com/sjhalayka/basic_fractals/blob/master/4d.cpp​

P.P.S. Here is the working quaternion Mandelbrot set: https://github.com/sjhalayka/basic_fractals/blob/master/mandelbrot.cpp​

..............................
..............**..............
.............****.............
............******............
............******............
............******............
............******............
...........********...........
..........**********..........
........**************........
........**************........
........**************........
......******************......
....**********************....
.....********************.....
.......****************.......
........**************........
.........************.........
........**************........
...........*......*...........
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................

taby said:
I must admit that I’ve never tried to make a quaternion Mandelbrot set, but what about the quaternion Julia sets for Z = Z^2 + C or like Z = sin(Z) + C sin(Z)? ? The quaternion fractals are so much cooler to look at than their 2D counterparts.

Quaternion Julia Set lacks the property to reveal new details if zooming in. Plotting iteration at one spot gives the same spirals as the 2D original, just with a constant rotation (axis of rotation remains constant due to the addition of a constant) and a sheer. This explains why the result looks like a revolved version of the 2D original.

I think we could get real details if the formula would generate those spirals at different 3D locations and orientations, not sharing them all the same plane, as it happens when replacing complex number with quaternion. I want it similar to real world galaxies.
To get there, i tried to calculate the centers of spirals, but did not find any working solution. Found some paper about those ‘points of convergence’, but did not work or i did it wrong.

Really interesting is real world architecture utilizing complex symmetries, like this in Iran:

Or Sagrada in Barcelona:

I'd love to see such things in games, and one could think it should be easier to make with the help of computers.

Fffff…. those are some deadly photos! Nice. ?

When you say quaternion Julia sets, in regard to the lack of small-scale detail, are you also talking about sets like Z = sin(Z) + C sin(Z)?