2D point is only for the example. In Minkowski Sum it is a point that is tested for collision(against volumes, not lines). So nothing bad with using a point.

If the point is perfectly lying on a line, you can arbitrarely decide what to do further. Treat it as a collision or a miss, it doesn't matter too much.

If you solved Minkowski Sum in 2D it is a matter of coding hours to solve it in 3D. No big mysteries.

Edit: extruding the walls of the shape into volumes works for both convex and concave shapes.

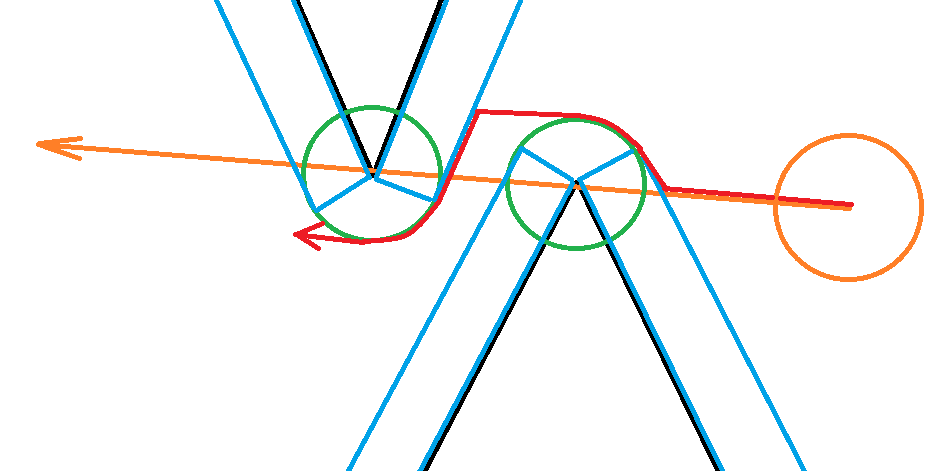
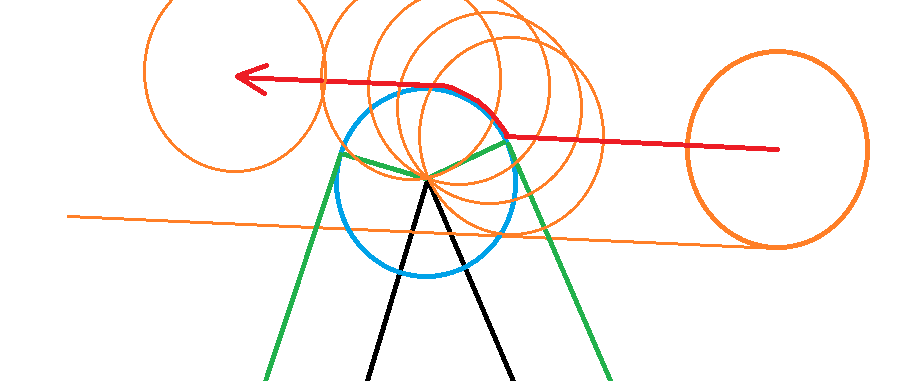
hi,

Here is some example code you might find helpful – I'm pretty confident there are no bugs since it's based on code I use, however I might have made some transcription errors.

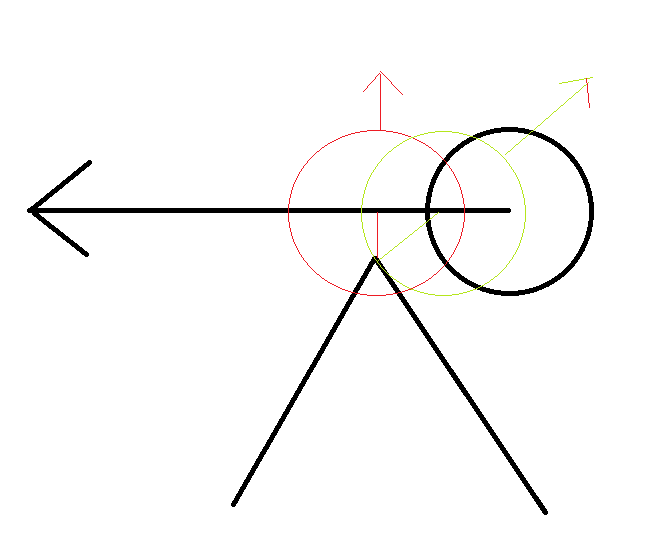
The basic method (calculate the distance to the closest point on the lineseg, then push the circle away from the lineseg, cancelling inwards velocity) is definitely correct though.

//basic collision detection+response for point-vs-lineseg: 
//	point(/circle) position p and velocity v
//	lineseg(/capsule) positions a,b
//	combined circle+capsule radius r (this needs to be >0 !)
//
//based on: //https://iquilezles.org/www/articles/distfunctions2d/distfunctions2d.htm
//
//NOTE: the exact same math should work in 3d, just swap vec2 with vec3
function DepenetrateAndSlide(p:vec2, v:vec2, a:vec2, b:vec2, r:float)
{
	vec2 pa = p-a;//delta vector from lineseg start to query point
	vec2 ba = b-a;//lineseg vector
	
	//"dot(pa,ba)/dot(ba,ba)" projects p onto the line containing ab, 
	//ie it's the distance from a to p, measured along the line containing ab,
	//in units "length of ab".
	//this means that if we clamp this parametric position to within [0,1]
	//we get a point on the lineseg -- h is the parametric position of the
	//closest point on the lineseg to p
	float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
	
	//note: the position of the closest-point-on-lineseg-to-p in
	//worldspace (ie nonparametric) is (a + ba*h)
	//(but we don't need that for our purposes)
	//
	//delta is the vector from the closest point on ab to p
	vec2 delta = pa - ba*h;
	
	float dlen = length(delta);
	float pen = dlen - r;
	if(pen < 0)
	{	
		//if we reached here, p is closer to ab than r
		//this means the circle is penetrating the capsule by -pen


		//n is the surface normal pointing outward from the lineseg
		vec2 n = delta/dlen;	
		
		//RESOLVE POSITION ERROR
		//push p along the normal, onto the outer surface of the capsule
		p -= n*pen;				
		
		float vn = dot(v,n);
		if(vn < 0)	
		{	
			//if we reached here, the circle's velocity is moving 
			//inward into the collision
		
			float bounce = 0;//0 is totally inelastic, 1 is totally elastic
			
			//RESOLVE VELOCITY ERROR
			//cancel the component of v that points along n
			v -= n*vn*(1+bounce);	
		}
	}
}

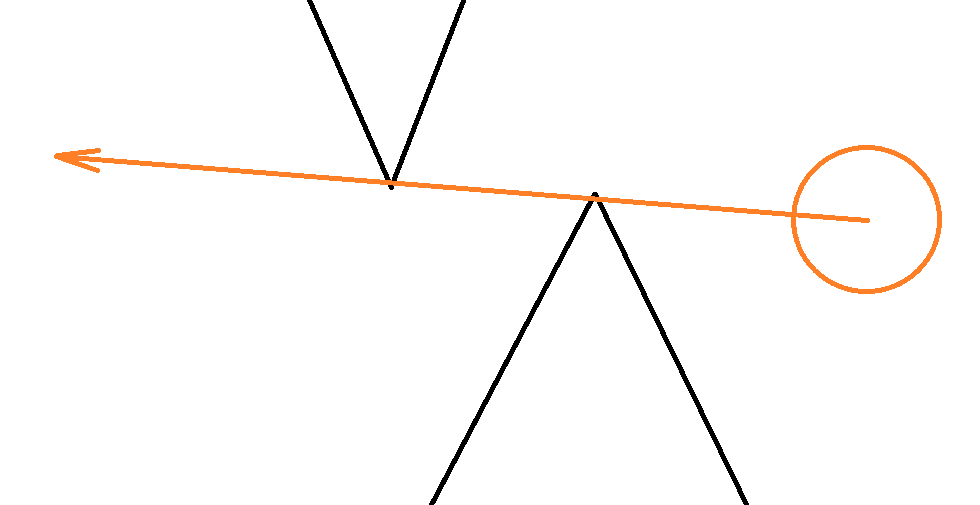
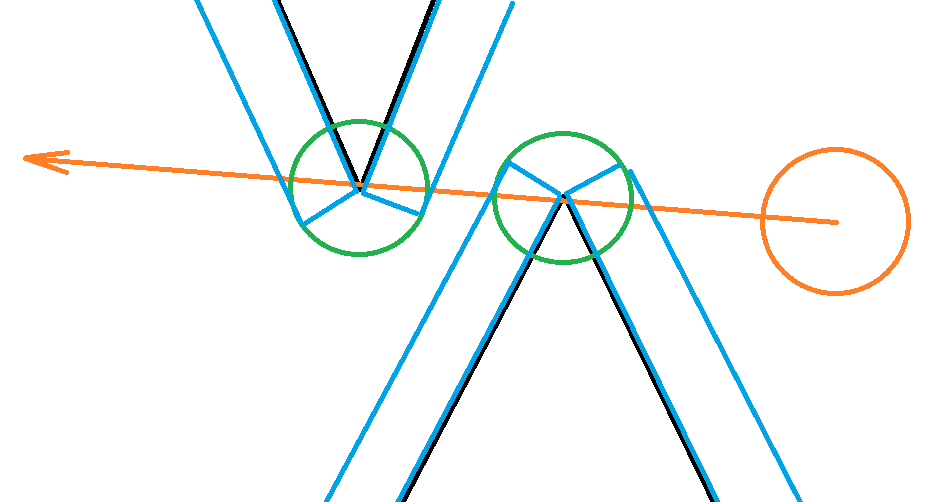
Hopefully this gives you some ideas. If the circle is colliding with multiple linesegs, it's not so trivial to resolve – one solution I've used in the past is:

1. record the circle's position
2. calculate the penetration for all colliding linesegs
3. push the circle out of the closest lineseg (ie correct the position error vs the lineseg with the most-negative pen value)
4. go to (2) unless we're not colliding with anything anymore
5. the vector from (1) to the circle's current position is an approximate normal; project the velocity onto this normal to cancel inward velocity.

(you could also skip (1) and (5) and instead correct the velocity error during (3), this works too, each process just gives slightly different results in cases with multiple collisions)

Good luck! : )

Raigan

This is my approach -

I checked my code now, i use no bias at no place never. Although the dilation is a kind of bias to be honest. It worked perfectly for any crazy shape i gave it, the bad thing is i have to parse the mesh. This is more work to do.

The same approach should work regardless of the shape, all you need is a way to determine the vector from the query point to the closest point on the surface of the shape, which lets you calculate the distance and the surface normal (which is what you need to de-penetrate and correct the velocity).

Possibly this won't apply to what you are doing but when I written systems to handle particle vs geometry collisions I introduced a sliding motion when the particles reached lower speed than a certain limit and then just applied friction for how it goes to a stop or slide/roll down an inclination.

What about moving sphere vertex collision ? How would i compute new sphere pos cause my actual code produces stuck jittering and once it pentrates it doesnt get out.

vec3 wd = FPP_CAM->pos + FPP_CAM->vel*dt;
vec3 pdst = ClosestPointOnLine(FPP_CAM->pos, wd, vec3(0.0, 0.0, 0.0));
float dst = n3ddistance(vec3(0.0, 0.0, 0.0), pdst);

if (dst <= scaled_radius)
{
float a = sqrt((scaled_radius*scaled_radius)-(dst*dst));
	FPP_CAM->pos = vec3(0.0, 0.0, 0.0)-normalize(vectorAB(FPP_CAM->pos, wd)*a*1.01;
} else 
FPP_CAM->pos = wd;

Its quite unreasonable for me:

Whenever collision occurs find closest point on movement line to vec(0,0,0) = pdst

Compute new sphere pos by basic trigonometry func aa+bb = cc

Where a = what we search for we move from pdst point towards FPP_CAM→pos start position) by this factor

b is diatance between vec3(0,0,0) and pdst

c is sphere radius

So it should move it away but i ifrwn get stuck inside what the hell??

I assume the problem is caused by making a line from velocity and limiting collision response to be tangent to that line. So you do the red approach in this picture:

But in fact the collision happens much earlier, causing a very different reaction force shown in green. (I've drawn it badly because the green collision falls into the edge region eventually, not the vertex region. But could happen for vertex region too.)
Notice in your approach the reaction depends on velocity which likely can cause jitter and issues. What if velocity is zero? What if velocity is normal to the plane of contact? In both cases there is no solution at all.

Coarsely speaking, there are two way to handle collisions:

1. The accurate one (similar to yours): Predict collisions, sort by time, integrate system to that first collision and resolve it, recalculate potential collisions and continue until given time step has been done. This can become very expensive with multiple dynamic bodies that collide with each other.

2. The gamey one: Integrate timestep, resolve collisions and done. There is no ordering and the time step is treated as a single moment with all collision events happening simultaneously.

The second option is easier to do, faster and more practical for realtime. It works as long as objects move slowly enough so they do not tunnel through other objects and missing the collision. To avoid this, either use smaller time steps or add a Continuous Collision Detection system (which i would not care about until needed).
So you could try that second approach and see if you like it more. Notice a sliding vector is not necessary to resolve penetration (but useful to model friction). In the above picture we would indeed miss the collision if the ball moves the whole black arrow so is very fast.

This paper shows a very simple physics solution: https://www.cs.cmu.edu/afs/cs/academic/class/15462-s13/www/lec_slides/Jakobsen.pdf​
Ignoring the verlet integration but paying attention to this image:

You can imagine how you get correct sliding behavior only from resolving penetration, without involving velocity or sliding vector calculations at all.

EDIT: From the age of my linked papers you see i may be a bit out of date ; ) There were people on the forum that know much better and could provide better help, but maybe they are all absent currently.

Just to clarify look at this drawing you made red line is pdst, green line is sphere_radius (scaled radius)

Now i move from pdst towards sphere start position to find point at which black and green line cross.

However this seems not working like expected. New velocity vector is projected onto green line normal

Theres also an issue when destination point can lay closer than sphere radius to vertex, rendering this aa + bb = cc useless

However i just wonder about thia jittering lets assume i alwyas go from right to left and colide with this vertex.. ok after first collision i move sphere out by its radius*1.01 this would give me a space (additionally if vel vector us big enough afternl projecting new vel it would move sphere slightly top-left) maybe thia causes jittering - maybe 1.01 is too big number etc etc.

Delta is fixed?

With dilation, the "game approach" works perfectly fine.

So if this is the case -

This is what happens under the hood -

There are tests for intersection of line with rectangle and line with circle(for 2D). Now it is much harder for it to tunnel through.

The red path is the solved one. It happened in a single time frame. No matter how far you attempt to go inside a single frame, it will compute it.

Sorry, i see now, my drawings are not quite the same case, but I will leave them there anyways. 
Here is a more similar case -

As i understand it, the OP attempts to make a player solve obstacles. Dilation works great for that, as the amount to dilate is the radius of the bounding circle of the player, and it usually is pretty big. Much bigger than the values people usually use as a bias.

(for 3D it is the same, just more codding. Lines/edges become cylinders, rectangle volumes become parallelepipeds, and point-corners become spheres. With the huge minus inherited - meshes/map need to be parsed. Once for static meshes, every time it changes for dynamic meshes.)