OK, so from the normal that we define as its x axis, we can find its y and z axis.
Now, with these 3 axis, how do we make rotations ?

we can find its y and z axes.

We can do this, but the result would be our arbitrary choice. So usually, what ever data you have already defines the full rotations, and there should be no need to ‘find’ anything.
E.g. you load transformation matrices per object from disk, or there are Euler angles which you convert to matrix on load.

ellenature said:
Now, with these 3 axes, how do we make rotations ?

float a = 0.3f; // some angle

vec3 quadOrn[3] = {
	(sin(a),cos(a),0),
	(-cos(a),sin(a),0),
	(0,0,1)
}; // our 3x3 matrix - quad is rotated by angle in z, but could have any other orientation

vec3 d (1,0,0); // some direction

vec3 d1 (quadOrn[0].dot(d), quadOrn[1].dot(d), quadOrn[2].dot(d)); // rotate our direction from global space into local space of our quad

vec3 d2 = d[0]*quadOrn[0] + d[1]*quadOrn[1] + d[2]*quadOrn[2]; // rotate direction from local space of quad into global space

I use array indices 0,1,2 to address x,y,z components for vectors.

Thank you for your help. I'll look into it.

If a rotation is applied to the object, do its three axis rotate with it or do they remain as they were at the beginning ?

They rotate (and also translate) with it.

I'm sorry, I'm still confused. How to get all three axis to rotate. Would you be okay with a voice call?

ellenature said:
How to get all three axis to rotate.

Because axis are just directions, you apply the same rotation to all 3 of them. (This is also what a matrix multiplication does.)

What you need is visualization, so you can do a bit trial and error and check the results.
Do you have this in your framework? Something to draw points, lines, triangles, usually done using OpenGL or DirectX?
With visual feedback everything about graphics and geometry becomes much easier. It's worth the time to set it up.

Voice call would become very expensive because i have no smart phone, but you can send PM if that helps.

Thank you very much for your help.
I will detail again the steps I take.
My square has a position in the world space and a direction (its normal).
I make the intersection with the ray and then I display the image.

t_bool	intersect_square(t_ray ray, t_square *square, t_intersection *inter)
{
	t_plane			plane;
	t_intersection	tmp_inter;
	int				ret;
	t_vec3			up;
	t_vec3			right;
	float			half_size;
	t_vec3			C1;
	t_vec3			C2;
	t_vec3			C3;
	float			X;
	float			Y;
	t_vec3			p;
	t_vec3			normal;

	normal = get_normalised(square->vec);
	plane.coord = square->coord;
	plane.vec = normal;
	ret = intersect_plane(ray, &plane, &tmp_inter);
	if (ret == FALSE)
		return (FALSE);

	right = vec_cross(normal, up);
	normalize(&right);
	up = vec_cross(right, normal);
	normalize(&up);
	half_size = square->side_size / 2;
	
	// calculation of 3 corners of the square
	C1 = vec_add(square->coord, vec_add(vec_mult(half_size, right), vec_mult(half_size, up)));
	C2 = vec_add(square->coord, vec_sub(vec_mult(half_size, right), vec_mult(half_size, up)));
	C3 = vec_sub(square->coord, vec_sub(vec_mult(half_size, right), vec_mult(half_size, up)));

	p = vec_add(ray.coord, vec_mult(tmp_inter.t, ray.dir));
	X = vec_dot(vec_sub(p, C1), vec_sub(C2, C1)) / get_norm_2(vec_sub(C2, C1));
	Y = vec_dot(vec_sub(p, C1), vec_sub(C3, C1)) / get_norm_2(vec_sub(C3, C1));
	if (X >= 0 &amp;&amp; X <= 1 &amp;&amp; Y >= 0 &amp;&amp; Y <= 1)
	{
		inter->t = tmp_inter.t;
		inter->normal = check_normal(ray, normal);
		inter->square = square;
		return (TRUE);
	}
	return (FALSE);
}

I press a key, this applies the rotation to the direction.

void		move_square(void *obj, int key)
{
	//t_vec3 up;
	float a = 0.3f;
	t_vec3	quadOrn[3] = {
		(sin(a),cos(a),0),
		(-cos(a),sin(a),0),
		(0,0,1)
	};
	
	if (key == KEY_L)
	{
		// I don't quite understand how to use d1.
		t_vec3 d1 = (t_vec3){vec_dot(quadOrn[0], ((t_square*)obj)->vec), vec_dot(quadOrn[1], ((t_square*)obj)->vec), vec_dot(quadOrn[2], ((t_square*)obj)->vec)};
		
		t_vec3 d2 = vec_add(vec_add(vec_mult(((t_square*)obj)->vec.x, quadOrn[0]), vec_mult(((t_square*)obj)->vec.y, quadOrn[1])), vec_mult(((t_square*)obj)->vec.z, quadOrn[2]));
		((t_square*)obj)->vec = d2;
	}

I apply the rotation to the director vector (normal of the square). Is that the problem ?
I don't think I'm using rotations well ?
And what about the rotation axis we talk about ?

I recalculate the intersection and display the image.

ellenature said:
My visual feedback

That's the raytraced framebuffer but no ‘debug visualization' like i mean.

Here's how it looks for me when i made raytracer for learning:

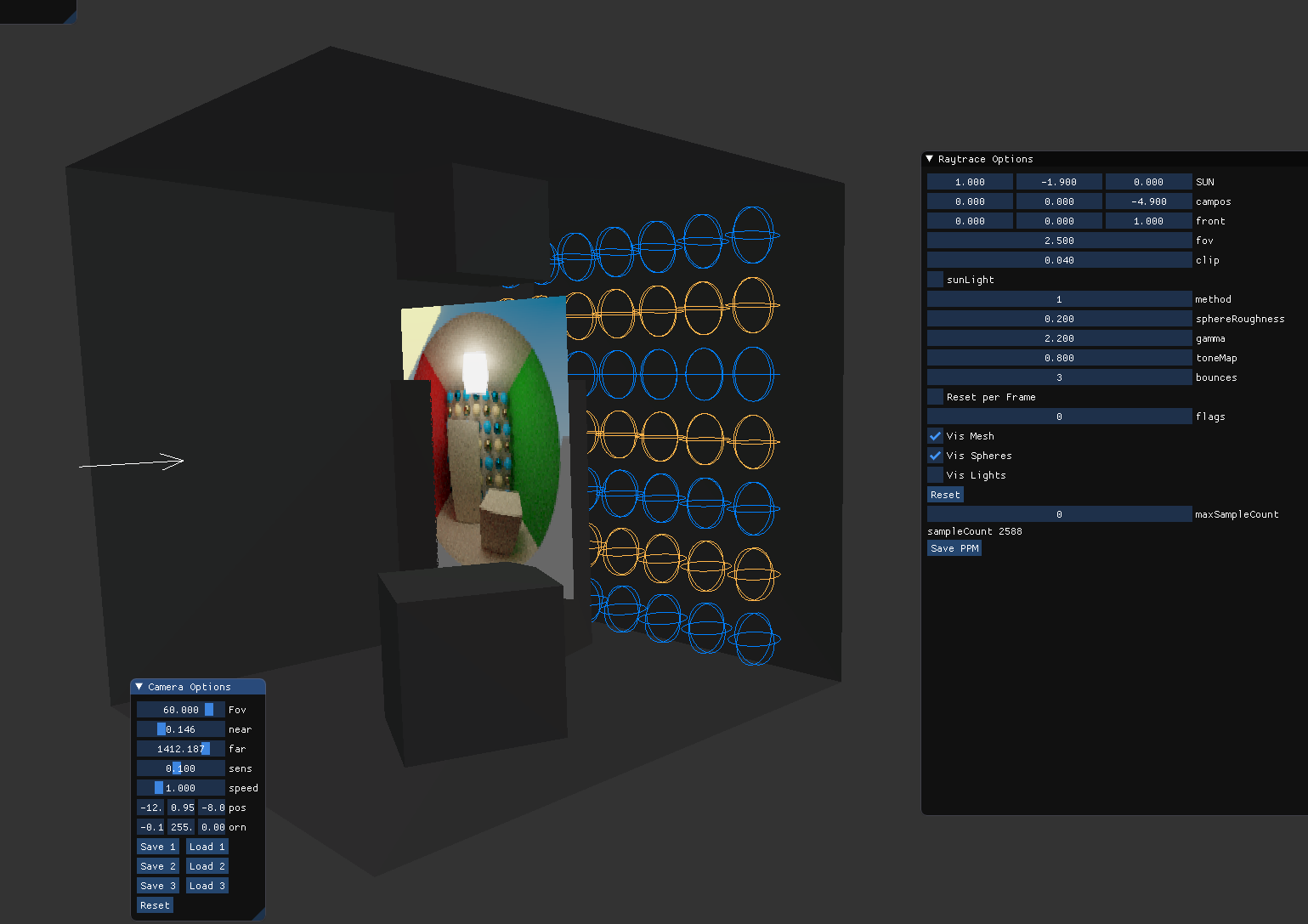
You see the RT framebuffer (spherical projection), white arrow is camera, then i have grey triangles for the Cornell box scene and colored circles showing the analytical spheres that i have added.

I can fly through the scene like in a video game, using WASD and mouse in realtime, while the raytracer is doing it's thing improving the image over time. I can also change various settings or variables using the GUI.

And i use this functionality for many things, e.g. i could visualize intersection calculations if i added a rectangle primitive, or i can show a single path from the raytracer. Seeing such things in 3D with ability to look at it from any angle is very helpful to proof things are where they should be, or to see what's wrong.

For me, this ‘realtime visual debugging’ became the most important debugging method, much more helpful than stepping through code or logging in most cases. And it's not much work to set it up, especially when using something like ImGui for the interface.

You would see very quickly how your rotation stuff works or not, what it is doing, and often that's enough to realize what the mistake is. Now you won't stop all work ind add this to your project right now, but just keep it in mind and consider to add such things at some time.

---

I see you construct the quad orientation using plane direction and up vector. That's fine, but you know that this causes flipping cases as the normal changes? And in case normal == upvector it would fail. To make this less likely happining, i propose to use a smaller angle than 0.3:

void		move_square(void *obj, int key)
{
	//t_vec3 up;
	float a = 0.01f;
	t_vec3	quadOrn[3] = {
		(cos(a),sin(a),0),
		(-sin(a),cos(a),0),
		(0,0,1)
	};
	
	if (key == KEY_L)
	{
		t_vec3 d = (t_square*)obj)->vec;
		t_vec3 rotatedD0 = vec_mult(d.x, quadOrn[0]);
		t_vec3 rotatedD1 = vec_mult(d.y, quadOrn[1]);
		t_vec3 rotatedD2 = vec_mult(d.z, quadOrn[2]);
		vec_add(rotatedD0, rotatedD1);
		vec_add(rotatedD0, rotatedD2);
		((t_square*)obj)->vec = rotatedD0;
	}

I think now it should rotate just a bit on each key press?

Notice i have also swapped cos and sin so the rotation matrix gives identity (doing nothing) if angle would be zero.

Problem with C alike vector math functions is that it becomes very hard to read with growing complexity. I did not try to understand what you did and have just rewritten it.

I tried with a vector (0,0,1) but my square disappears.
The calculation returns a vector (0,0,0)