Hello guys! I was tasked to do a morphing animation of a ring/torus 3D mesh for a webgl application. The shapes that it needs to go over are predefined by my client and it's going to be switching randomly between one and the others. At first I thought it was going to be a trivial task, but all the things I tried didn't really work out and now I'm out of ideas, so I came here to ask the experienced people for advice.

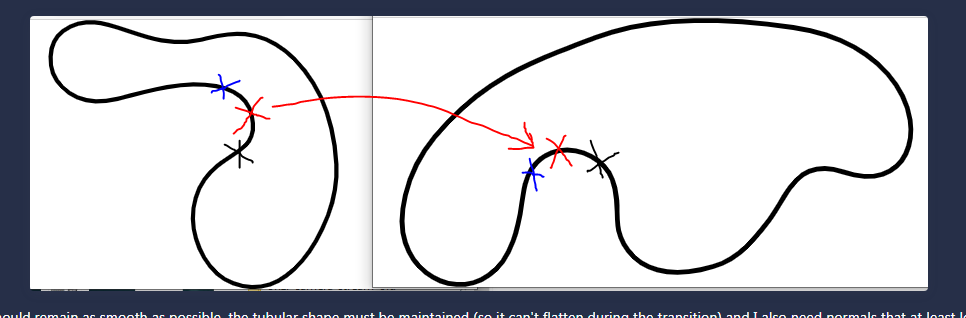
Below I describe the things that I tried and the problems I had, but before that, here are some 2D screenshots of the kind of shapes I'm working with:

A few things to keep in mind that are important, when morphing the shapes should remain as smooth as possible, the tubular shape must be maintained (so it can't flatten during the transition) and I also need normals that at least look correct (because I need to apply lighting to it)

Now, the things I've tried:

1- GPU Blendshapes: this was the very first thing I tried, I just made the 3D shapes in maya with the same amount of vertices, and interpolated between them in the vertex shader, and quickly this exposed all of the problems that I would end up having with all remaining solutions.

The “length” of the shapes wasn't the same, so a lot of stretching was visible, and also because the start of the shape wasn't in the same place as the other, the vertices would fly all over the screen, losing the tubular shape. I tried fixing this by creating both shapes from the ‘almost’ same starting point and similar length, but the tubular shape was always lost in some places more than others. I ended up discarding this solution.

2- On the fly mesh generation: Since this is the only thing the app will be doing, I decided to try and generate the geometry of the shape every frame. I used an array of points representing each curve, interpolated these points, and using the resulting points to generate a smooth curve with a catmull-rom spline, and then feeding the spline to a 3D extrusion algorithm that generates the 3D shape.

This presented most of the same problems than the previous technique, but gave better results since now the stretching wasn't as noticeable, and the shape was ‘almost’ maintained during the transition. But I had additional problems with normals not being smooth enough, thus the lighting made it obvious that there were a lot of discontinuities and sharp turns (even though the catmul rom should have smooothed out most of it). I think the extrusion algorithm couldn't handle well the sharp turns, and unfortunately the library I'm using only provides catmull-rom splines (I tried searching for other libraries but none of them were well documented).

3- Bone based animation: this one seemed promising but it failed pretty quick. I set up a torus with 20-30 bones and tried to deform them with a keyframe animation. It was extremely difficult avoiding the stretching when moving the bones, although maybe I was doing it wrong and there is another way, since I'm not too experienced with these tools (I used maya).

I can, of course, put constraints on the kind of shapes that we should doif that is needed for this to work (like all shapes being the same length, which I'm sure it must be essential at this point). If you have any other ideas (or think I could improve on the ones I used) please let me know!

Cheers

There is a lot of research about morphing one shape to another.

The usual steps are to make a bijective mapping between them and build a topologically equivalent parametrization for both.
What this means is to have a mapping from each point of one shape to a point on the other shape, and adjacent points on the first point are also adjacent with the corresponding points on the other shape in the same order.

For your case (which i assume is just closed 2D curves), such mapping would look like this:

Red points are shown with the mapping to the other shape, and adjacent points (blue and black) are direct neighbors of the red point, with consistent clockwise order.

It's somewhat obvious, but exactly what you need, and terms might help to look for some papers…

What i would do now is something like this:

1. Subdivide both curves to the same number or vertices and edges, to get a discretization of the smooth curves.
2. Calculate curvature for each vertex from its direct neighbors, smooth it to a periodic low frequency signal, and match resulting minimas or maximas to get the ‘most important’ corresponding points on the other shape. (Would give us the red points as above because they are the strongest bumps.)
3. We can now morph the loops to each other. Extrude the edge loops to get a torus like mesh.

The problem to optimize morphing animation so it minimizes energy to look natural reminds me on this blog post: http://kirilllykov.github.io/blog/2014/01/17/curvature-flow-in-curvature-space/​​

Good luck, surely no easy problem : )

Thanks a lot! I will do some research