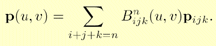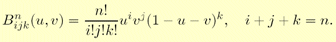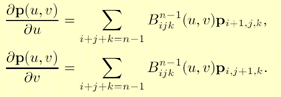Hi there, everyone!
I am programing a tessellation shader in OpenGL which computes the quartic Walton-Meek's Gregory patch. I am searching for a local G1 method with good shading/visual results. So I am trying this patch. I didn't get good (visual/shading) results with PN-Triangles.
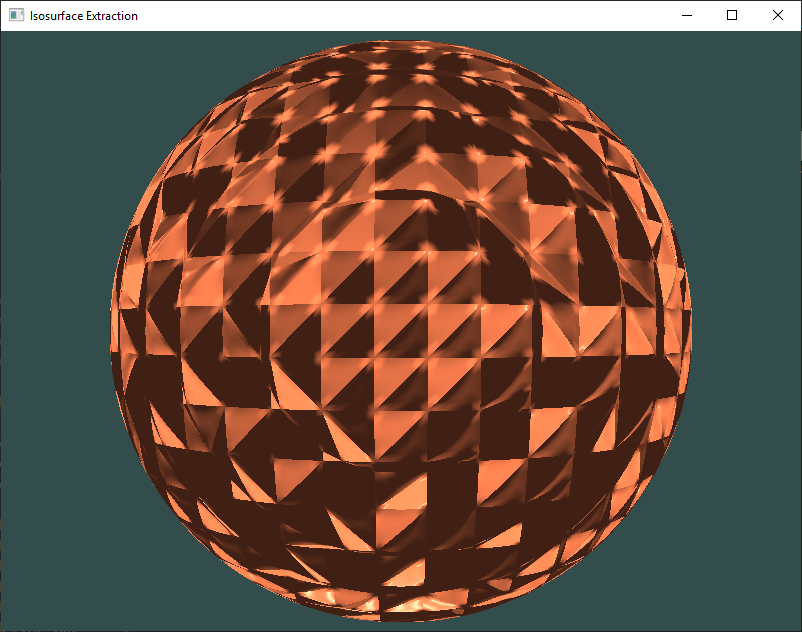
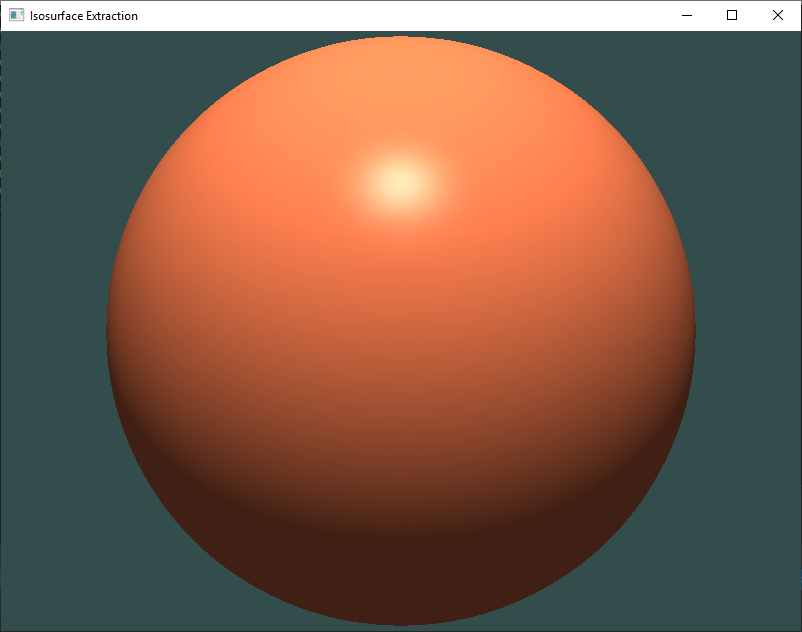
I've just had my first result with this WM patch, which isn't good as well. Perhaps the normal I am calculating is wrong. I will attach the equations I am using to compute the normal. Please, take a look there as I couldn't write in TeX here (I don't know why). Basically, they are the Bernstein polynomial, Bernstein-Bezier triangle and its derivatives. Then, I actually compute it through normalizing the cross product between the derivatives.
If you want to take a look at the shader code, here it is (the first one is the tessellation control shader and the second one is the tessellation evaluation shader):
#version 430 core
layout (vertices = 3) out;
in VertOut
{
vec3 normal;
} vertOut[];
out TescOut
{
vec3 p0;
vec3 p1;
vec3 p2;
vec3 p3;
vec3 g0;
vec3 g1;
vec3 n;
} tescOut[];
void main()
{
const float kTessLevel = 12.0;
gl_TessLevelOuter[gl_InvocationID] = kTessLevel;
gl_TessLevelInner[0] = kTessLevel;
vec3 p0 = tescOut[gl_InvocationID].p0 = gl_in[gl_InvocationID].gl_Position.xyz;
vec3 n = tescOut[gl_InvocationID].n = vertOut[gl_InvocationID].normal;
const int nextInvID = gl_InvocationID < 2 ? gl_InvocationID + 1 : 0;
vec3 edge = gl_in[nextInvID].gl_Position.xyz - p0;
vec3 nNext = vertOut[nextInvID].normal;
float d = length(edge), a = dot(n, nNext);
vec3 gama = edge / d;
float a0 = dot(n, gama), a1 = dot(nNext, gama);
float ro = 6.0 * (2.0 * a0 + a * a1)/(4.0 - a * a);
float sigma = 6.0 * (2.0 * a1 + a * a0)/(4.0 - a * a);
vec3 v[4] = vec3[4]
(
p0,
p0 + (d / 18.0) * (6.0 * gama - 2.0 * ro * n + sigma * nNext),
gl_in[nextInvID].gl_Position.xyz - (d / 18.0) * (6.0 * gama + ro * n - 2.0 * sigma * nNext),
edge = gl_in[nextInvID].gl_Position.xyz
);
vec3 w[3] = vec3[3]
(
v[1] - v[0],
v[2] - v[1],
v[3] - v[2]
);
vec3 A[3] = vec3[3]
(
cross(n, normalize(w[0])),
vec3(0.0),
cross(nNext, normalize(w[2]))
);
A[1] = normalize(A[0] + A[2]);
vec3 l[5] = vec3[5]
(
v[0],
0.25 * (v[0] + 3.0 * v[1]),
0.25 * (2.0 * v[1] + 2.0 * v[2]),
0.25 * (3.0 * v[2] + v[3]),
v[3]
);
vec3 p1 = tescOut[gl_InvocationID].p1 = l[1];
vec3 p2 = tescOut[gl_InvocationID].p2 = l[2];
vec3 p3 = tescOut[gl_InvocationID].p3 = l[3];
barrier();
const int previousInvID = gl_InvocationID > 0 ? gl_InvocationID - 1 : 2;
vec3 D[4] = vec3[4]
(
tescOut[previousInvID].p3 - 0.5 * (p0 + p1),
vec3(0.0),
vec3(0.0),
tescOut[nextInvID].p1 - 0.5 * (p3 + tescOut[nextInvID].p0)
);
float mi[2] = float[2](dot(D[0], A[0]), dot(D[3], A[2]));
float lambda[2] = float[2](dot(D[0], w[0])/dot(w[0], w[0]), dot(D[3], w[2])/dot(w[2], w[2]));
tescOut[gl_InvocationID].g0 = 0.5 * (l[1] + l[2]) + (2.0/3.0) * (lambda[0] * w[1] + mi[0] * A[1]) + (1.0/3.0) * (lambda[1] * w[0] + mi[1] * A[0]);
tescOut[gl_InvocationID].g1 = 0.5 * (l[2] + l[3]) + (1.0/3.0) * (lambda[0] * w[2] + mi[1] * A[2]) + (2.0/3.0) * (lambda[1] * w[1] + mi[1] * A[1]);
}
#version 430 core
layout(triangles, equal_spacing, ccw) in;
in TescOut
{
vec3 p0;
vec3 p1;
vec3 p2;
vec3 p3;
vec3 g0;
vec3 g1;
vec3 n;
} tescOut[];
out TeseOut
{
vec3 normal;
vec3 viewPosition;
} teseOut;
uniform mat4 mvp;
uniform mat4 modelView;
uniform mat4 normalMatrix;
uniform bool isNormalLinearlyInterpolated;
#define uvw gl_TessCoord
const float u = uvw.x, u2 = u * u, u3 = u2 * u, u4 = u2 * u2;
const float v = uvw.y, v2 = v * v, v3 = v2 * v, v4 = v2 * v2;
const float w = uvw.z, w2 = w * w, w3 = w2 * w, w4 = w2 * w2;
#define p400 tescOut[0].p0
#define p310 tescOut[0].p1
#define p220 tescOut[0].p2
#define p130 tescOut[0].p3
#define G01 tescOut[0].g0
#define G02 tescOut[0].g1
#define p040 tescOut[1].p0
#define p031 tescOut[1].p1
#define p022 tescOut[1].p2
#define p013 tescOut[1].p3
#define G11 tescOut[1].g0
#define G12 tescOut[1].g1
#define p004 tescOut[2].p0
#define p103 tescOut[2].p1
#define p202 tescOut[2].p2
#define p301 tescOut[2].p3
#define G21 tescOut[2].g0
#define G22 tescOut[2].g1
#define B400 u4
#define B040 v4
#define B004 w4
#define B310 (4.0 * u3 * v)
#define B031 (4.0 * v3 * w)
#define B103 (4.0 * u * w3)
#define B220 (6.0 * u2 * v2)
#define B022 (6.0 * v2 * w2)
#define B202 (6.0 * u2 * w2)
#define B130 (4.0 * u * v3)
#define B013 (4.0 * v * w3)
#define B301 (4.0 * u3 * w)
#define B211 (12.0 * u2 * v * w)
#define B121 (12.0 * u * v2 * w)
#define B112 (12.0 * u * v * w2)
#define B300 u3
#define B030 v3
#define B003 w3
#define B210 (3.0 * u2 * v)
#define B021 (3.0 * v2 * w)
#define B102 (3.0 * w2 * u)
#define B120 (3.0 * u * v2)
#define B012 (3.0 * v * w2)
#define B201 (3.0 * w * u2)
#define B111 (6.0 * u * v * w)
vec3 interpolate3D(vec3 p0, vec3 p1, vec3 p2)
{
return gl_TessCoord.x * p0 + gl_TessCoord.y * p1 + gl_TessCoord.z * p2;
}
void main()
{
vec4 pos = vec4(interpolate3D(tescOut[0].p0, tescOut[1].p0, tescOut[2].p0), 1.0);
vec3 normal = normalize(interpolate3D(tescOut[0].n, tescOut[1].n, tescOut[2].n));
if (u != 1.0 && v != 1.0 && w != 1.0)
{
vec3 p211 = (v * G12 + w * G21)/(v + w);
vec3 p121 = (w * G02 + u * G11)/(w + u);
vec3 p112 = (u * G22 + v * G01)/(u + v);
vec3 barPos = p400 * B400 +
p040 * B040 +
p004 * B004 +
p310 * B310 +
p031 * B031 +
p103 * B103 +
p220 * B220 +
p022 * B022 +
p202 * B202 +
p130 * B130 +
p013 * B013 +
p301 * B301 +
p211 * B211 +
p121 * B121 +
p112 * B112;
pos = vec4(barPos, 1.0);
vec3 dpdu = p400 * B300 +
p130 * B030 +
p103 * B003 +
p310 * B210 +
p121 * B021 +
p202 * B102 +
p220 * B120 +
p112 * B012 +
p301 * B201 +
p211 * B111 ;
vec3 dpdv = p310 * B300 +
p040 * B030 +
p013 * B003 +
p220 * B210 +
p031 * B021 +
p112 * B102 +
p130 * B120 +
p022 * B012 +
p211 * B201 +
p121 * B111 ;
normal = normalize(cross(dpdu, dpdv));
}
gl_Position = mvp * pos;
pos = modelView * pos;
teseOut.viewPosition = pos.xyz / pos.w;
teseOut.normal = (normalMatrix * vec4(normal, 0.0)).xyz;
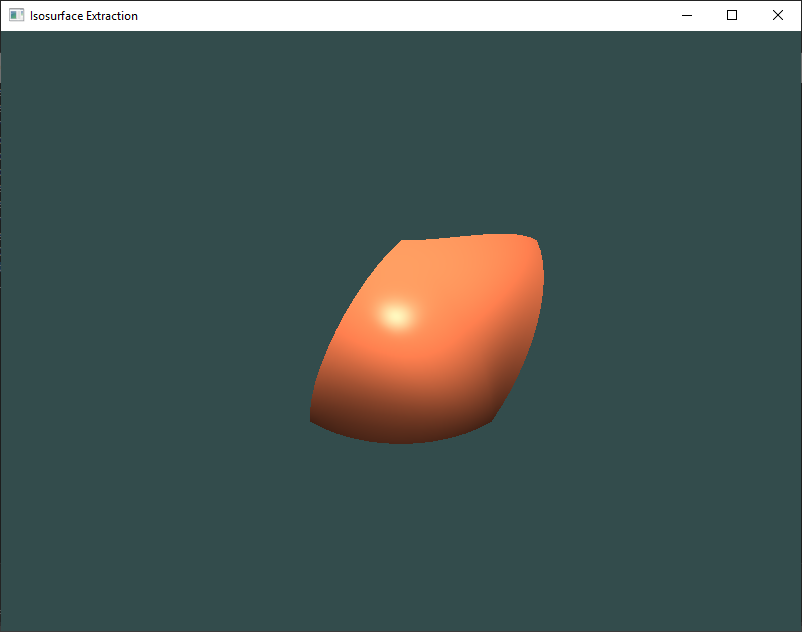
}There are also some screenshots attached of my current results. Please, take a look. In the "good ones" images, the normals are computed by linear interpolation, while in the bad ones the normals are computed through the equations I said previously and are shown in the code.
So, how can I correctly compute the normals? Thanks in advance!