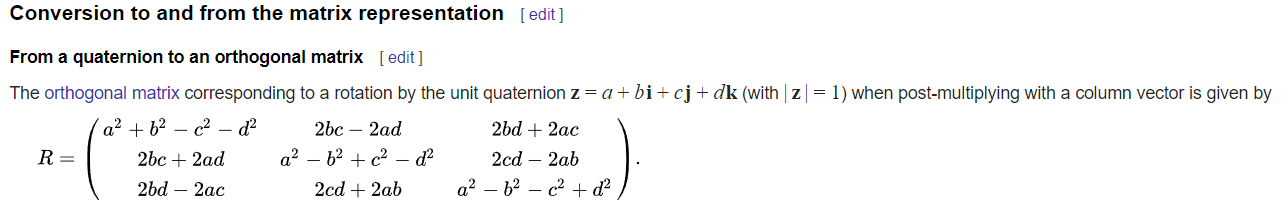I don't understand why calculating the world space inverse inertia tensor with R*I*R^T doesn't work. It has the same effect as using only I. The only way I can get it to work is to transpose all my quaternion derived matrices, including the ones used for rendering, but then all rotations are negated. Otherwise I have to use R*I.
I've checked all functions involved in the calculation countless times. Maybe my coordinate system handedness is inconsistent, but I don't know where. My intention is to use a right-handed coordinate system, with x pointing to the right, y down and z away from the user. Matrices are row-major.
Some relevant functions:
Matrix3x3 Matrix3x3::Rotate(const Quaternion& quaternion)
{
Matrix3x3 result;
float xx = quaternion.X * quaternion.X;
float yy = quaternion.Y * quaternion.Y;
float zz = quaternion.Z * quaternion.Z;
float xy = quaternion.X * quaternion.Y;
float wz = quaternion.Z * quaternion.W;
float xz = quaternion.Z * quaternion.X;
float wy = quaternion.Y * quaternion.W;
float yz = quaternion.Y * quaternion.Z;
float wx = quaternion.X * quaternion.W;
result.M11 = 1.f - 2.f * (yy + zz);
result.M12 = 2.f * (xy + wz);
result.M13 = 2.f * (xz - wy);
result.M21 = 2.f * (xy - wz);
result.M22 = 1.f - 2.f * (zz + xx);
result.M23 = 2.f * (yz + wx);
result.M31 = 2.f * (xz + wy);
result.M32 = 2.f * (yz - wx);
result.M33 = 1.f - 2.f * (yy + xx);
return result;
}
Matrix3x3 Matrix3x3::Scale(const Vector3& v)
{
return Matrix3x3(
v.X, 0.f, 0.f,
0.f, v.Y, 0.f,
0.f, 0.f, v.Z);
}
Vector3 operator *(const Matrix3x3& m, const Vector3& v)
{
return Vector3(
Vector3::Dot(m.Row(0), v),
Vector3::Dot(m.Row(1), v),
Vector3::Dot(m.Row(2), v));
}
I also checked qu3e a bit more thoroughly than the first time, but couldn't find any relevant differences in the calculations. The ones I found didn't make a difference.