Space partition data structures are used in different fields such as collision detections, ray casting, and to perform efficient spatial queries. There are different data structures to partition the space, each one with cons and pros (QuadTrees, BSP, k-d trees, Bounding Volume hierarchy, grid, etc). In this case we propose a new type of grid space partition, where we can recursively divide the cells into new grids. The main objective of this data structure is to optimize the performance and memory usage in comparison with the normal grid space partitions.
Flat grids
Flat grids data structure are a very easy to implement and very fast when performing different queries. The main problem with this data structure is that it's good only when the elements are uniformly distributed in space. Suppose the next example:

Where each box represent an object and the grid (cells numbered from 0 to 15) represents the game world (where the entities can move for example). In this particular case a flat grid will be fine since all the entities can move around all the world space. But, there are some cases where the level is not fully available for the entities, there are some parts of the world where the entities cannot move around (a big river, buildings, forests, etc). We represent these things with red-cells in the next image:
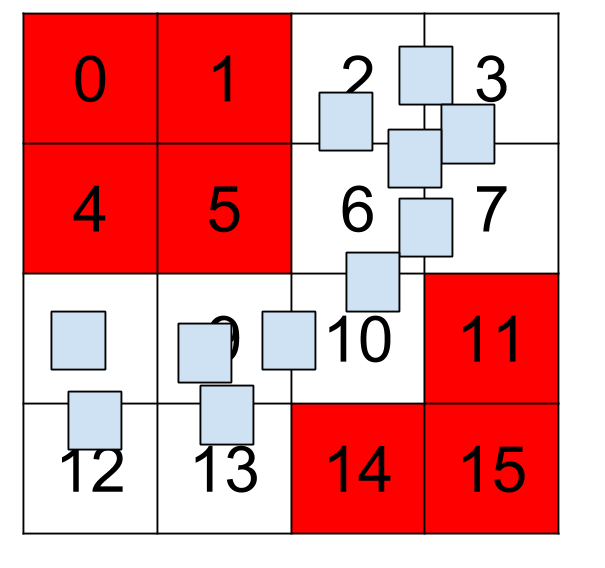
In such cases we are wasting memory since those cells will be never used.
Multilevel grid
To improve these situations we propose a multi-level grid space partition. The concept is simple, and we will show it with images. For the example shown above, we can first divide the matrix into four cells:
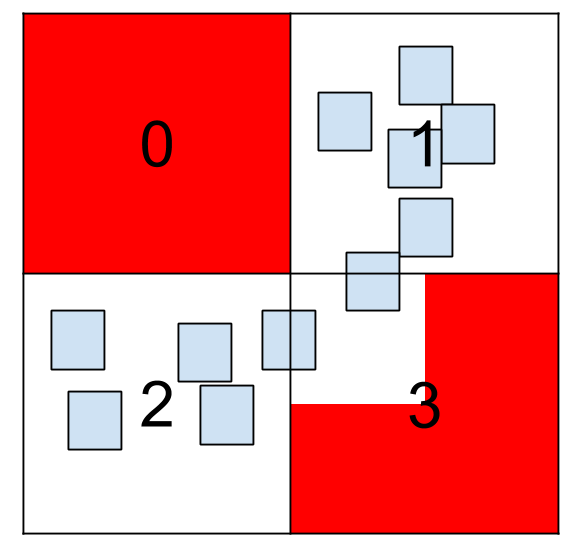
We can see that for cell 0 nothing will be never inside of it, so basically this cell is discarded for further subdivisions. Also, entities will be able to move on cell 3 only around the "white" space, so the real "valid space" of that cell is 1/4 of cell 3 size (assuming we discretize the space in Bounding Boxes). We can check also that cell 1 and 2 are the most used by the entities. For those cases we want to subdivide into more cells again. We can do it in different ways, the next image is one example of all those possibilities:
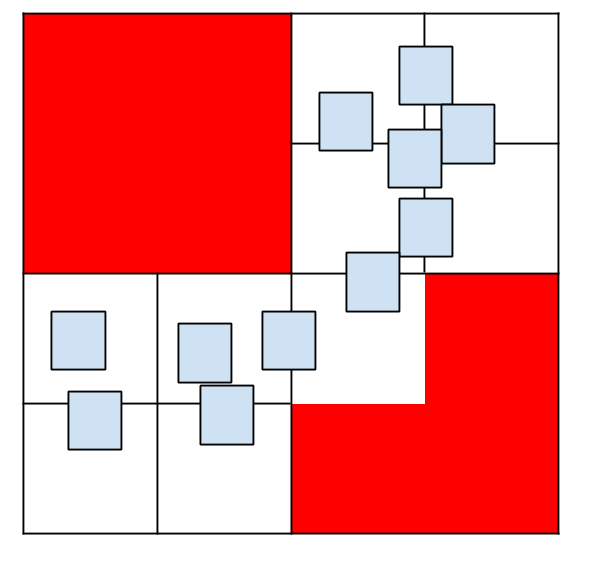
In this case what we did was: Subdivide the cells 1 and 2 (of first divisions image) into 4 cells and leave cells 0 and 3 as they were. For this case we have a total of 12 cells (4 cells in the first division and 8 cells in the second subdivision). Note that we are free to subdivide each cell as we want, it is not necessary to divide each cell with the same amount of rows and columns. We can think of each cell as a new "world" and then work on them recursively. In this example we save a total of 4 cells, having the same performance in Big O notation (we can access a cell in constant time with a factor of 2 instead of 1). Note that the factor will be associated with the number of subdivisions (deep in the hierarchy). In almost all the cases the number of subdivisions will be small (if we subdivide cells into 4 - 2 rows x 2 columns - recursively we will end up with performance similar to a Quadtree). Someone can think that this is waste of time and we are complexifying a problem too much for a very poor memory gain, for sure that for this particular example it isn't worth it, but for big scenarios these multi-level subdivisions can guide us to improve a lot in memory and time space.
Conclusion
In this short article we present an idea to optimize particular cases of the normal flat grid space partition, where using the same amount of memory we can increase substantially the performance of the "spatial queries". One interesting point about this data structure is that it could be automatically generated without big complications. From a list of entities sizes (bounding boxes) and static objects / unavailable parts of the level, we can calculate a good space division. Obviously for an optimum one we need to provide more information like a simulation of entities movement around the world. But this is another topic and something that should be analyzed in another article :). In https://github.com/agudpp/MGSP you can find the source code for this data structure (under development!).






I don't think it's helpful at all to have an article this short without any data to back it up. How fast is this compared to having fixed-depth quadtree? How much memory does this save? How do you efficiently flatten and expand each node when objects are added/removed/moved?