My approach to this problem is to design a way of reducing this explosion in memory requirements and still get decent speed and graphics while using hard disks (since it is cheaper per megabyte) for storing the majority of the graphics. I'm also interested in making the algorithm so that game designers can use a more dynamic set of tiles (in size and type) and still be safely within the memory constraints of their consumer's system.
[size="5"]How would this be done?
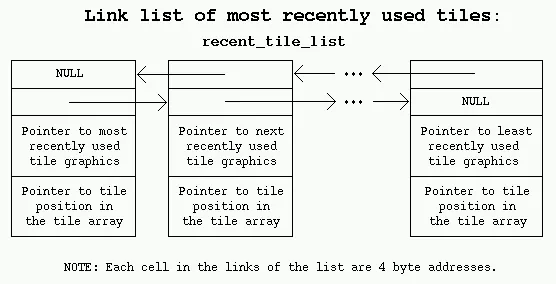
I propose using a combination of two common data storage types: an array (for fast random access), and a bi-directional linked list (for quickly determining the tile used in the most distant past). Variables are also used to store the number of tiles loaded, and the addresses at the beginning and end of the linked list. (For memory usage, I'm assuming a 32bit word size with 32bit addressing.)
The array is used as a quick reference for grabbing the tiles. Each tile is given a location in the array. When the tile needs to be accessed, the tile's position in the array is checked. If the position stores a NULL pointer, then the tile's graphics need to be loaded from the hard disk into the memory cache. If the position stores a pointer to a node in the linked list, then that node has the cached graphic, so it doesn't need to be reloaded from the hard disk.
The linked list is used to store the graphics in order of most recently to least recently used (LRU) tiles in the cache. This order helps to keep tiles that are used often or are more likely to be used in the future since they were used recently. Those tiles which were not used recently are replaced with the tiles that need to be cached.
The nodes have pointers to the previous and next nodes so that they can be quickly removed from the list (we have a pointer to the previous node, so we can make it point to the node after the current node; and we have a pointer to the next node, so we can make it point to the node before the current node). They also have pointers to the position they hold in the array, so if they are removed from the list (normally when they are the last element and are discarded for adding a new tile), the corresponding location in the array can be given a NULL pointer immediately. The pointer to the graphic points to the information necessary for drawing the tile (or you can put the graphic information directly in that place if you want to save the time needed to redirect the pointer).
Whenever a tile is used, the graphic is accessed through the linked list. If it's not in the linked list, it must be added. If a new tile is added to the list, the least recently used tile's array location is set to NULL, and it is removed from the list. The newly created node becomes the most recently used node, is loaded with the graphic's data, and has it's address added to the tile's location in the array. If a graphic is already in the linked list, it's node is just moved from it's current position to the recently used node position in the list.
You must be careful to correctly update the most recently used and the least recently used tile pointers correctly. Whenever something is moved to the top of the list, the most recently used pointer must be updated. Whenever a node's pointer to the next node is made NULL, the least recently used pointer must point to that node.
[size="5"] What does this technique give us?
Assuming that each element in the array is about 4 bytes (maybe 8 bytes if we need some extra information for loading the graphics off the hard disk), we would have (4 * number_of_tiles) bytes used by the array. This becomes our only value dependent on the number of tiles, so assuming that we would normally have stored all of the tiles in memory ahead of time (each tile is probably bigger than 16 bytes), we're saving a great deal of memory! The rest of the memory can be used for the cache which only holds those tiles currently in use. This means our usage of memory will also be more efficient (less waste). Each node only takes up about (4 * 4 bytes) = (16 bytes) plus the memory required to store the graphic. Notice that the amount of memory used by the node is minuscule in comparison to the memory used by a graphic, so it can be generally neglected.
[size="5"] Need more speed!
The downfall of this technique is the number of pointers that need to be manipulated and copied. It's not an unreasonable amount of pointers to deal with, but there are ways to reduce the number of times we have to move a node in the linked list. There are many cases where a group of tiles naturally follow each other in close proximity. By making each node contain multiple tiles (making them point to the most recently used tile set), we can avoid moving nodes if the tile being drawn is followed by another tile in its own set (this is because it would be in the most recently used node which doesn't need to be moved, it's already in the correct position).
Another idea would be to give each node a dirty bit (flag). When you move the node to the most recent position, you set the dirty bit (on), and know not to move it again until the dirty bit is reset (off). Before a period of getting tiles, you first clear all of the dirty bits (which will only be in the nodes at the beginning of the list, so you don't have to go through the entire list), then start accessing the tiles. This means each node will only move once per session and you will avoid redundantly moving nodes.