taby said:
The more fractional the dimension, the less fractal the curve
A book with that sound title will sell more copies than General Jists. : )
Me, imagining 2.5D before reading the book:

…after reading the book:

taby said:
The more fractional the dimension, the less fractal the curve
A book with that sound title will sell more copies than General Jists. : )
Me, imagining 2.5D before reading the book:

…after reading the book:

LOL!
No seriously, these count as vacuum solutions. Now, to model a galaxy, which is not a vacuum. :)
Oh yes, I forgot to mention that I found fractal behaviour when analyzing the data.
The paper is at: https://github.com/sjhalayka/papers/blob/main/review/bezier_escape.pdf
The next three images show how fractal behaviour is found when multiplying the intersection count (e.g. field strength) by the inverse falloff. These are the last three figures in the paper.
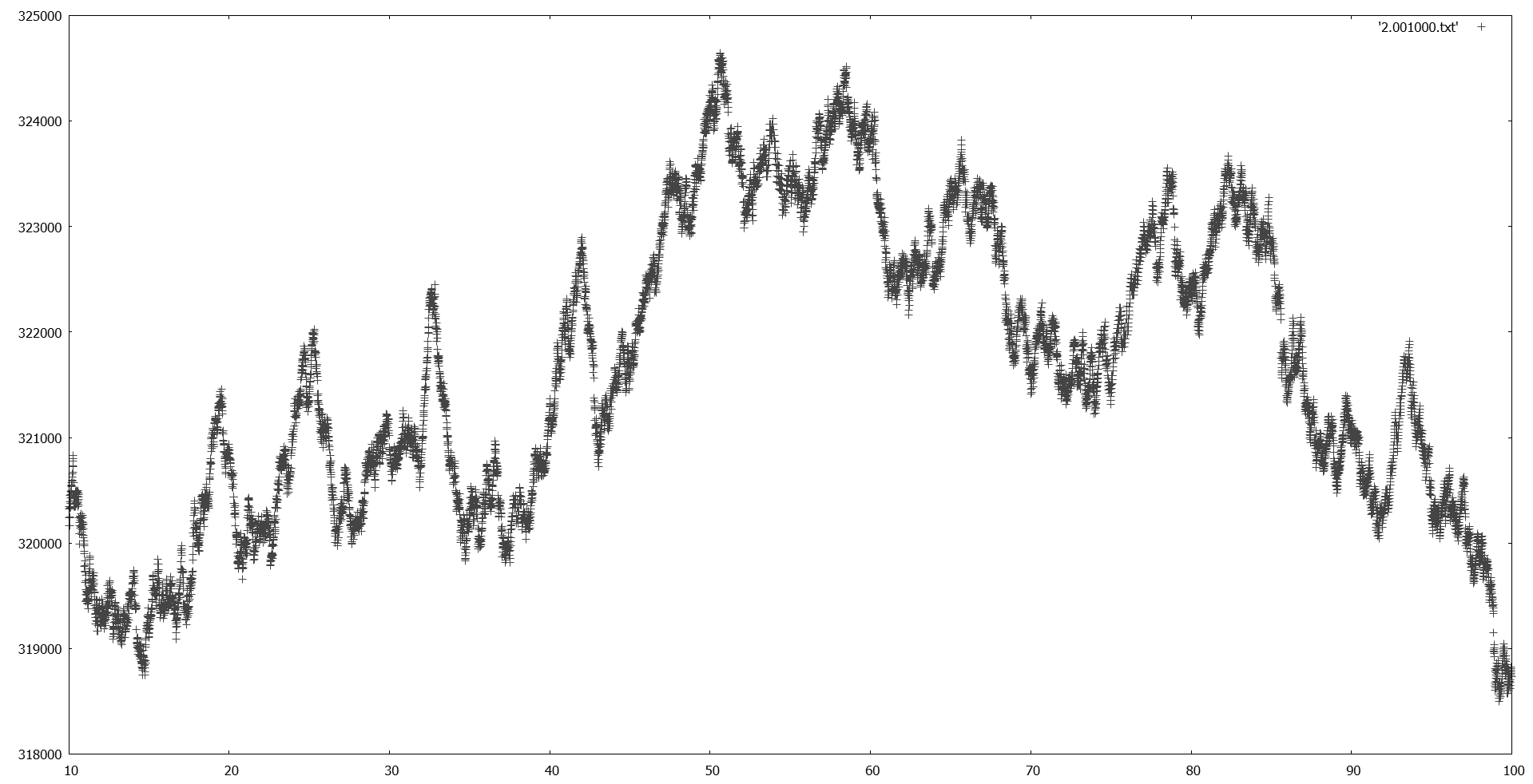
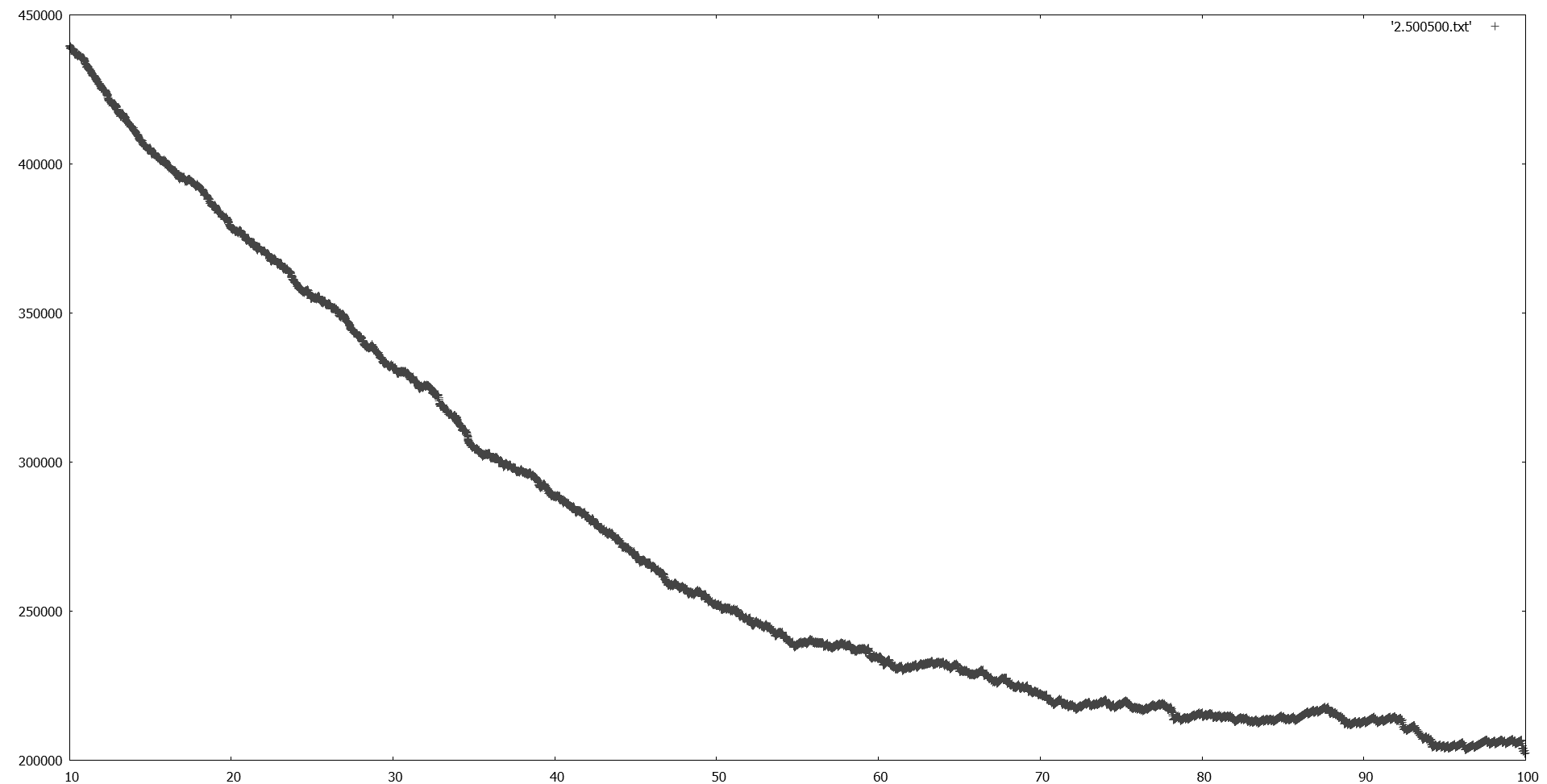
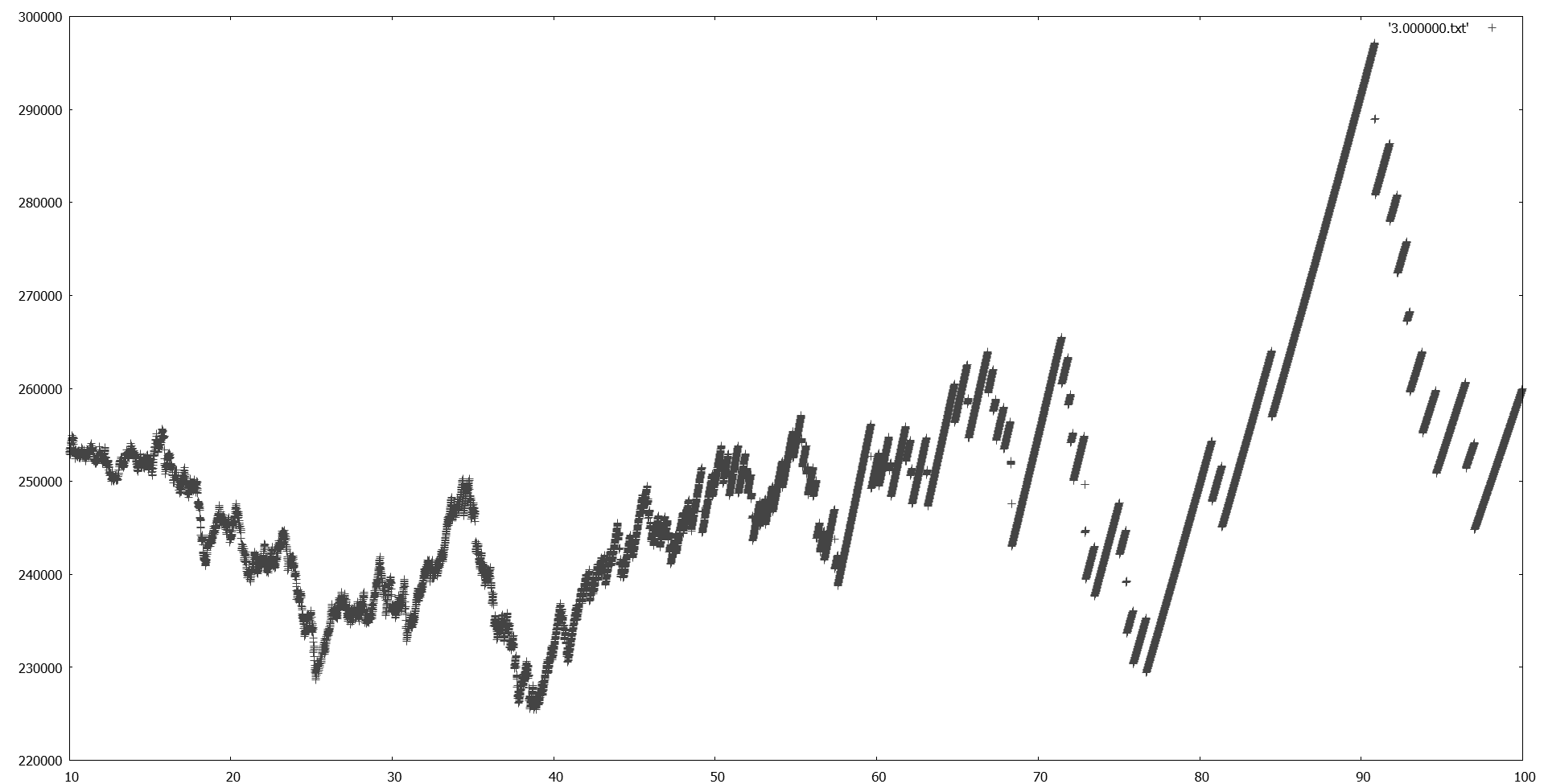
That last plot looks like Minecraft Farlands or Z-fighting artifacts.
Is it fractal, or is it floating point precision limits? : )
Yes good idea. I tried using long doubles but there is no visible difference.
For fun, I also ran the data through R, and it produces the same plot as gnuplot. So it’s definitely inherent to the data.
Edit: Looks non-fractal in the end. :)
OK, so I've got it working now! It's a bit hectic, but it basically goes to show that G*M is a constant.
@undefined You made a diagram which makes it clear that you are looking for the distance from a point to the surface of an ellipse (or ellipsoid) in N dimensions.
This is a hard problem! Even in 2D, it doesn’t have an analytical solution.
Your best option is to write an algorithm which makes a guess and then refines it for as many iterations as you can spare.
Your initial guess can be the nearest point on the sphere, in a space which has been scaled to turn the ellipsoid surface into a sphere.
You can then transform that point back into a point on the surface of the ellipse, and see how much you miss the original point by when you trace out along the normal at that point.
Measuring this orthogonal error can be used to add a shift to update your guess, after which you can repeat the whole process again.
After your iteration has converged enough for your purposes, you can use the distance between the final guess and your query point to calculate whatever kind of falloff you want.
Thanks for your comment.
I'm not quite sure what you mean, for the most part. I don't need to space the points out evenly using repulsion, where n ≥ 10000000 or whatever, because they come out evenly spaced in the long run.
I calculate the ray-sphere intersections. I use these to get the gradient at some distance r, which I multiply by r^D, where D is the dimension of the gravitational field.