In a previous article, the problem of hitting a target with a fixed velocity was discussed and a solution described. In that case, the shooter had the ability to launch the projectile immediately at the direction where the target would eventually intercept it. While this is true for many cases, it is also true that the effect of having an AI turn and shoot at a moving target, and hit it, is more realistic and just plain awesome. It raises the bar significantly above "shoot at stuff" to "I can pick which target I want to hit, turn to shoot at it before it knows what's going on, and move on to the next target with ease." As you would expect, this does raise the bar a bit in the algorithm area.

Approaching the Problem

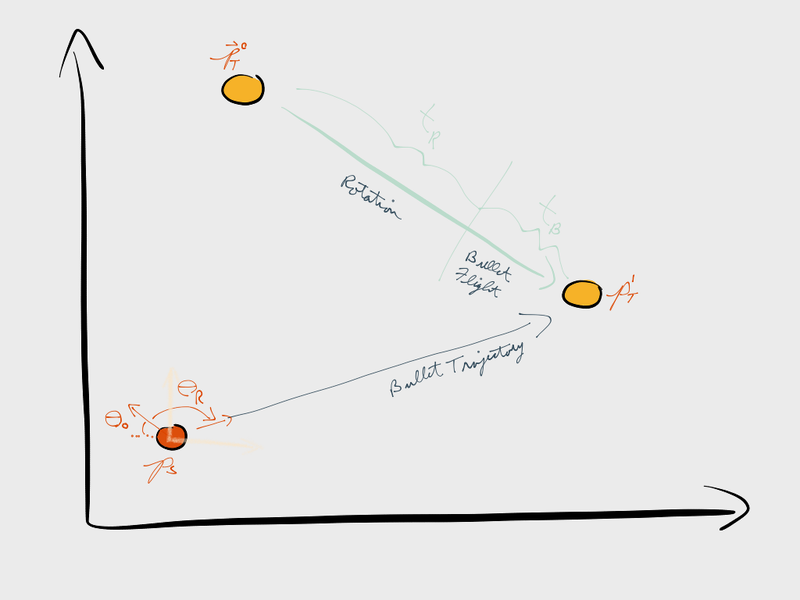
Looking at the picture below, it can be seen that the dynamics of the problem are very similar to the case from before. The equations derived in the previous article still describe the situation: (1) \(\vec{P_T^1} = \vec{P_T^0} + \vec{v_T} *(t_B+t_R)\) (2) \((P_{Tx}^1 - P_{Sx})^2 +(P_{Ty}^1 - P_{Sy})^2 = S_b^2 * (t_B+t_R)^2\) However, now instead of the time being just \(t_B\), the term includes \(t_R\), which is the amount of time needed to rotate through \(\theta_R\) radians. Defining a few new variables:

1. The unit vector for the "facing" direction of the shooter when the calculation begins: \(\hat{P_{ST}^0}\)
2. The unit vector for the "facing" direction of the shooter when the shot is fired; this points towards \(\vec{P_T^1}\): \(\hat{P_{ST}^1}\)
3. The rate at which the shooter rotates its body: \(\omega_R\)

When the body rotates at a rate of \(\omega_R\) for \(t_R\) seconds, it rotates through \(\theta_R\) radians. \(\omega_R * t_R =\theta_R\) Given the unit vectors defined above and using the definition of the dot product: (3) \(\omega_R * t_R = acos(\hat{P_{ST}^0}\cdot\hat{P_{ST}^1})\) In the previous case, the situation was "static". You fire the projectile and it heads towards a location. The only thing you need to know is the time of flight. But now you need to know how long you have to wait before you can shoot. But the longer you wait, the further your target will have traveled. So the solution "moves" as the rotation time increases. That is a fairly "ugly" set of equations to try and solve. The static case's quadratic solution and evaluation of its descriminant gave us a good picture of the number of solutions possible. In this case, because of the quadratic/transcendental nature of the formuals, there may or may not be a closed form solution to it. So what do we do? Instead of asking ourselves how can we find the answer directly, ask ourselves how we would know if we found an answer that worked at all.

Pick A Number Between...

If we were to pick a random number for the total time, \(t_{impact} = t_R + t_B\), we could calculate the intercept position because that is how far the target would have traveled in that time, equation (1). Since we know the final position, we can calculate how far the projectile must have traveled to hit the target and also the time to rotate to that position from (2) and (3). If the value we chose for \(t_{impact}\) is a solution, then: \(t_{impact} = t_R + t_B\) But, if it is not, then \(t_{impact}\) will either be greater than or less than the sum. Using this, we can propose an answer, test it, and decide if that answer lies to the "left" or "right" of the proposed solution. Then propose (read: guess) again, using the answer we just got to get a little closer. Using this approach, we can iterate towards a solution in a (hopefully) bounded number of steps. Not as clean as a simple "plug and chug" formula, but very serviceable.

Binary Search

It is tempting to use a fast-converging numerical technique like Newton's Method to try and solve this. But the shape of the space that the solution lies in is unknown. We haven't even proven that the "left" or "right" decision process won't stick us in some thorny cyclic patch of non-convergence. Shooting off towards infinity on a small derivative estimate is also something that would be undesirable and hard to bound. We want this to be executed in an AI for a game that is running out in the field, not in a lab. So, we're going to trade something that *might* converge faster for a search algorithm that will guarantee cutting the search space in half each time, the binary search. Here is how it will work:

1. Define the minimum value, \(t_{min}\) that will be the smallest value for \(t_{impact}\) that will be allowed.
2. Define the maximum value, \(t_{max}\) that will be the largest value for \(t_{impact}\) that will be allowed.
3. Start with the value that is between the minimum and maximum as the first proposed value.
4. Loop:
   1. Calculate the final impact location.
   2. Calculate the rotation time necessary to face the impact location, \(t_{rot}\).
   3. Calculate the flight time from the shooter to the final impact location, \(t_{flight}\).
   4. \(t_{shot} = t_{impact} - (t_{rot} + t_{flight})\)
   5. if \(t_{shot} > 0\), then set the upper limit to the proposed value and propose a new value between the upper and lower limits.
   6. if \(t_{shot} < 0\), then set the lower limit to the proposed value and propose a new value between the upper and lower limits.
   7. If the value of value of \(t_{impact}\) is changing within less than a specified tolerance, the algorithm has converged.
   8. If the number of loops gets too high, fail.
5. Return success and the final position or failure.

The Code

The following function calculates whether or not the target can be hit and then returns the result. If the target could not be hit, the return value is "false". If it could, the return value is "true" and the solution, the position vector of the impact. /* Calculate the future position of a moving target so that * a turret can turn to face the position and fire a projectile. * * This algorithm works by "guessing" an intial time of impact * for the projectile 0.5*(tMin + tMax). It then calculates * the position of the target at that time and computes what the * time for the turret to rotate to that position (tRot0) and * the flight time of the projectile (tFlight). The algorithms * drives the difference between tImpact and (tFlight + tRot) to * zero using a binary search. * * The "solution" returned by the algorithm is the impact * location. The shooter should rotate towards this * position and fire immediately. * * The algorithm will fail (and return false) under the * following conditions: * 1. The target is out of range. It is possible that the * target is out of range only for a short time but in * range the rest of the time, but this seems like an * unnecessary edge case. The turret is assumed to * "react" by checking range first, then plot to shoot. * 2. The target is heading away from the shooter too fast * for the projectile to reach it before tMax. * 3. The solution cannot be reached in the number of steps * allocated to the algorithm. This seems very unlikely * since the default value is 40 steps. * * This algorithm uses a call to sqrt and atan2, so it * should NOT be run continuously. * * On the other hand, nominal runs show convergence usually * in about 7 steps, so this may be a good 'do a step per * frame' calculation target. * */ bool CalculateInterceptShotPosition(const Vec2& pShooter, const Vec2& vShooter, const Vec2& pSFacing0, const Vec2& pTarget0, const Vec2& vTarget, float64 sProjectile, float64 wShooter, float64 maxDist, Vec2& solution, float64 tMax = 4.0, float64 tMin = 0.0 ) { cout << "----------------------------------------------" << endl; cout << " Starting Calculation [" << tMin << "," << tMax << "]" << endl; cout << "----------------------------------------------" << endl; float64 tImpact = (tMin + tMax)/2; float64 tImpactLast = tImpact; // Tolerance in seconds float64 SOLUTION_TOLERANCE_SECONDS = 0.01; const int MAX_STEPS = 40; for(int idx = 0; idx < MAX_STEPS; idx++) { // Calculate the position of the target at time tImpact. Vec2 pTarget = pTarget0 + tImpact*vTarget; // Calulate the angle between the shooter and the target // when the impact occurs. Vec2 toTarget = pTarget - pShooter; float64 dist = toTarget.Length(); Vec2 pSFacing = (pTarget - pShooter); float64 pShootRots = pSFacing.AngleRads(); float64 tRot = fabs(pShootRots)/wShooter; float64 tFlight = dist/sProjectile; float64 tShot = tImpact - (tRot + tFlight); cout << "Iteration: " << idx << " tMin: " << tMin << " tMax: " << tMax << " tShot: " << tShot << " tImpact: " << tImpact << " tRot: " << tRot << " tFlight: " << tFlight << " Impact: " << pTarget.ToString() << endl; if(dist >= maxDist) { cout << "FAIL: TARGET OUT OF RANGE (" << dist << "m >= " << maxDist << "m)" << endl; return false; } tImpactLast = tImpact; if(tShot > 0.0) { tMax = tImpact; tImpact = (tMin + tMax)/2; } else { tMin = tImpact; tImpact = (tMin + tMax)/2; } if(fabs(tImpact - tImpactLast) < SOLUTION_TOLERANCE_SECONDS) { // WE HAVE A WINNER!!! solution = pTarget; return true; } } return false; }

The algorithm takes not only the position of the shooter, but its velocity as well. This is provision for a small modification where the shooter could be moving. In development of Star Crossing thus far, it has not been necessary to put in this modification. Feel free to let us know via feedback if you work it in (and it works for you).

The Video

Instead of cooking up a video just to demonstrate the basic use of the algorithm, it is going to be more effective to let you see it in action. The video below is a clip from a game we are actively working on called Star Crossing. In the clip, the ship pulls the Defense Drone behind it like a tail gunner. The Defense Drone turns to shoot at the Snakes as the ship drags it around. Go about a minute into the video and you'll see it.

This game is in work and the art is all drawn by hand to have something to look at while the mechanics are worked out. It looks pretty...well...crayolaish...that's not even a word but it probably has the right feel. If you would like to help the project with some art skill, feel free to contact us.

The Demo

I put together a small console application as a test bed to develop the algorithm initially. The simulation allows you to tinker with the parameters and see the running of the algorithm. You can download the source code for it using the link below. It is written in C++ and should compile on any modern compiler. We used XCode on a Macbook Pro, but the code has no graphics or special libraries associated with it.

The (Rest of the) Code

Get the Source Code for this article hosted on GitHub by clicking here.

Interesting Points

• While there is a bound on the algorithm, it usually converges in less than 10 steps in our testing.
• (Proposed...not proven) Knowing your turn rate in radians/sec, you can modify the SOLUTION_TOLERANCE_SECONDS value so that it converges to a resoluion in terms of arc seconds from the target. That is to say, you don't have to shoot dead at the target positiion to hit it, you just have to be really close. This gives you a good way to set your tolerance and save some loops. You could change the algorithm to take a tolerance in degrees or radians to set the convergence limit.
• You need to handle the case where the target is heading right at you. We use the dot product for this and just "fire now". This is done before the algorithm is even called.
• Our initial algorithm shot at the location of the target instead of leading it. When we put the new algorithm into effect at first, it was not too exciting, but much better. When we put in the "shoot if it is in front of you" addition, the combo pack was devastating and we had to turn down the Defense Drone weapon power to stop it from decimating the snakes too fast. Be careful what you wish for.
• While I haven't tried it, it seems reasonable you could pick a "better" start value for \(t_{impact}\) by using the non-rotating solution plus a little slop time (maybe the amount of time to rotate to face that position). This has the right "feel" for an initial estimate and seems worth exploring in the future.

Conclusion

This article presented an approach for predicting the future position of a moving target based on having to rotate to shoot it. A simulation of using the algorithm was also created for you to tinker with. The solution appears to work well for our current needs.

Article Update Log

30 October 2014: Initial release