- Non-Rotating Shooter
- Rotating Shooter
- The position of the shooter when the projectile will be launched: \(\vec{P_s}\)
- The position of the target when the shooter will launch the projectile (i.e. now): \(\vec{P_T^0}\)
- The speed at which your projectiles travel: \(S_b\)
- The velocity of the target, \(\vec{v_T}\)
The Problem Space
Consider the image below: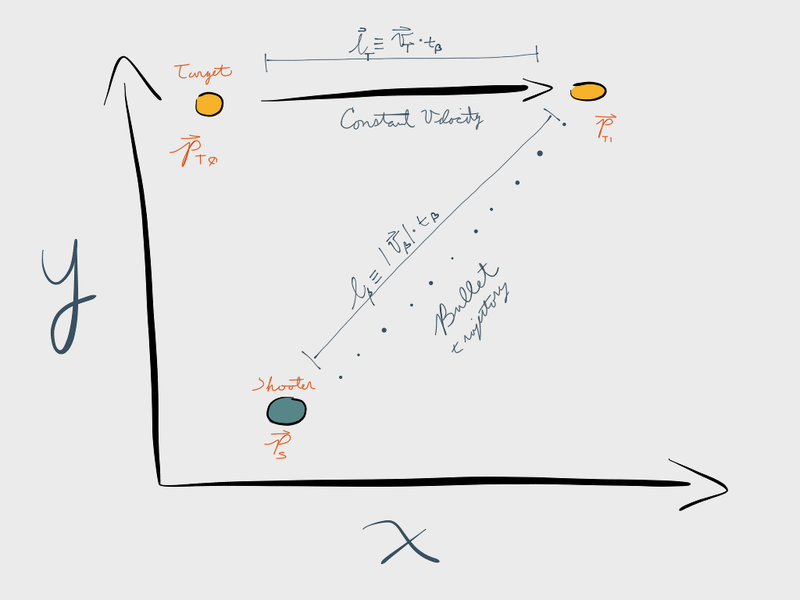
This image shows the situation for the shooter. The target is moving with some constant velocity and the intercept position for the projectile, when launched, is unknown until the calculation is done. When the projectile is launched, it will intercept the target after \(t_B\) seconds. The projectile is launched with a constant speed. We don't know its direction yet, but we know the magnitude of its velocity, its speed will be \(S_b\).
If the target is at position \(\vec{P_T^0}\) now, it will be at position \(\vec{P_T^1}\), given by:
(1) \(\vec{P_T^1} = \vec{P_T^0} + \vec{v_T} * t_B\)
Since the projectile will have traveled for the same amount of time, it will have moved from \(\vec{P_s}\) to \(\vec{P_T^1}\) as well. In that time, it will have moved a distance of \(S_B x t_B\). Since we are talking about vector quantities here, we can write this as:
\(\mid\vec{P_T^1}-\vec{P_s}\mid = S_b * t_B\)
If we square both sides and break it into components to get rid of the absolute value:
(2) \((P_{Tx}^1 - P_{Sx})^2 +(P_{Ty}^1 - P_{Sy})^2 = S_b^2 * t_B^2\)
Breaking (1) into components as well and substituting back into (2) for the value of \(P_{Tx}^1\) and \(P_{Ty}^1\), we get the following:
\((P_{T0x} - P_{Sx} + v_{Tx}t_B)^2 + (P_{T0y} - P_{Sy} + v_{Ty}t_B)^2 = S_b^2 * t_B^2\)
For the sake of simplicity, we going to redefine:
\(P_T^0 - P_s = R \)(this is a constant)
After some algebra, this gives us the final equation:
\(t_B^2(v_{Tx}^2 + v_{Ty}^2-S_B^2) + t_B(2*R_x*v_{Tx} + 2*R_y*v_{Ty}) + (R_x^2 + R_y^2) = 0\)
This is a quadratic in \(t_B\):
\(t_b = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
where:\( a =v_{Tx}^2 + v_y^2-S_B^2\)
\( b =2(R_x*v_{Tx} + R_y*v_{Ty})\)
\( c = R_x^2 + R_y^2\)
You can test the discriminant, \(b^2-4ac\):
< 0 \(\Rightarrow\) No Solution.
= 0 \(\Rightarrow\) One solution.
> 0 \(\Rightarrow\) Two solutions, pick the lowest positive value of \(t_B\).
Once you have solved the quadratic for \(t_B\), you can then substitute it back into (1) and calculate the intercept position, \(\vec{P_T^1}\).
The Code
Putting this together and covering some edge cases:
/* Calculate the future position of a moving target so that
* a projectile launched immediately can intercept (collide)
* with it.
*
* Some situations where this might be useful for an AI to
* make this calculation.
*
* 1. Shooting a projectile at a moving target.
* 2. Launching a football or soccer ball to a player.
* 3. Figuring out the best position to jump towards in
* a platform game.
*
*
* The output value, solution, is the position that the
* intercept will occur at and the location that the
* projectile should be launched towards.
*
* The function will return false if a solution cannot
* be found. Consider the case of a target moving away
* from the shooter faster than the speed of the
* projectile and you will see at least one case where
* this calculation may fail.
*/
bool CalculateInterceptShotPosition(const Vec2& pShooter,
const Vec2& pTarget0,
const Vec2& vTarget,
float64 sProjectile,
Vec2& solution
)
{
// This formulation uses the quadratic equation to solve
// the intercept position.
Vec2 R = pTarget0 - pShooter;
float64 a = vTarget.x*vTarget.x + vTarget.y*vTarget.y - sProjectile*sProjectile;
float64 b = 2*(R.x*vTarget.x + R.y*vTarget.y);
float64 c = R.x*R.x + R.y*R.y;
float64 tBullet = 0;
// If the target and the shooter have already collided, don't bother.
if(R.LengthSquared() < 2*DBL_MIN)
{
return false;
}
// If the squared velocity of the target and the bullet are the same, the equation
// collapses to tBullet*b = -c. If they are REALLY close to each other (float tol),
// you could get some weirdness here. Do some "is it close" checking?
if(fabs(a) < 2*DBL_MIN)
{
// If the b value is 0, we can't get a solution.
if(fabs(b) < 2*DBL_MIN)
{
return false;
}
tBullet = -c/b;
}
else
{
// Calculate the discriminant to figure out how many solutions there are.
float64 discriminant = b*b - 4 * a * c;
if(discriminant < 0)
{ // All solutions are complex.
return false;
}
if (discriminant > 0)
{ // Two solutions. Pick the smaller one.
// Calculate the quadratic.
float64 quad = sqrt(discriminant);
float64 tBullet1 = (-b + quad)/(2*a);
float64 tBullet2 = (-b - quad)/(2*a);
if((tBullet1 < 0) && (tBullet2 < 0))
{ // This would be really odd.
// Both times are negative.
return false;
}
else if(tBullet2 < 0 && tBullet1 >= 0)
{ // One negative, one positive.
tBullet = tBullet1;
}
else if(tBullet1 < 0 && tBullet2 >= 0)
{ // One negative, one positive.
tBullet = tBullet2;
}
else if(tBullet1 < tBullet2)
{ // First less than second
tBullet = tBullet1;
}
else
{ // Only choice left
tBullet = tBullet2;
}
}
else
{
tBullet = -b / (2*a);
}
}
// If the time is negative, we can't get there from here.
if(tBullet < 0)
{
return false;
}
// Calculate the intercept position.
solution = pTarget0 + tBullet*vTarget;
return true;
}
I have posted a working solution, with a simulation of using the above function and which you can tinker with, on github.
I would not have guesses that it will be so complicated, but it is really useful, thanks!