I have a code to calculate inverse square falloff, but it's not working as I had hoped. Any big ideas? For instance, where dimension == 3, the falloff should be proportional to 1/r^2.
vector_3 get_random_point_in_ellipse(double radius_a, double radius_b)
{
double rho = static_cast<double>(rand() % RAND_MAX) / static_cast<double>(RAND_MAX);
double phi = 2.0 * pi * static_cast<double>(rand() % RAND_MAX) / static_cast<double>(RAND_MAX);
vector_3 point;
point.x = sqrt(rho) * cos(phi);
point.y = sqrt(rho) * sin(phi);
point.x = point.x * radius_a;
point.y = point.y * radius_b;
return point;
}
double get_antiparallelity_from_unnormalized_vectors(vector<vector_3> vectors)
{
double antiparallelity = 0;
size_t count = 0;
for (size_t i = 0; i < vectors.size(); i++)
vectors[i].normalize();
for (size_t i = 0; i < vectors.size() - 1; i++)
{
for (size_t j = (i + 1); j < vectors.size(); j++)
{
// antiparallelity
const double d = 1.0 - abs(vectors[i].dot(vectors[j]));
antiparallelity += d;
count++;
}
}
//cout << count << " " << vectors.size() * (vectors.size() - 1) / 2.0 << endl;
antiparallelity /= count;
return antiparallelity;
}
double antiparallelity_from_ellipse(const double x_radius, const double emitter_distance, const double dimension)
{
ellipse_points.clear();
for (size_t i = 0; i < n; i++)
{
const double dimension_diff = 1.0 - (3.0 - dimension);
double x_radius = 1.0;
ellipse_points.push_back(get_random_point_in_ellipse(x_radius, dimension_diff * x_radius));
}
for (size_t i = 0; i < ellipse_points.size(); i++)
ellipse_points[i].z = -emitter_distance;
return get_antiparallelity_from_unnormalized_vectors(ellipse_points);
}
int main(int argc, char** argv)
{
cout << setprecision(20) << endl;
srand(static_cast<unsigned int>(time(0)));
double dimension = 2.0; // between 2 and 3
for (double i = 1; i < 1e10; i += 1e2)
{
const double exponent = dimension - 1.0;
cout << i << " " << antiparallelity_from_ellipse(1.0, i, dimension) / pow(i, exponent) << endl;
}
...
return 0;
}

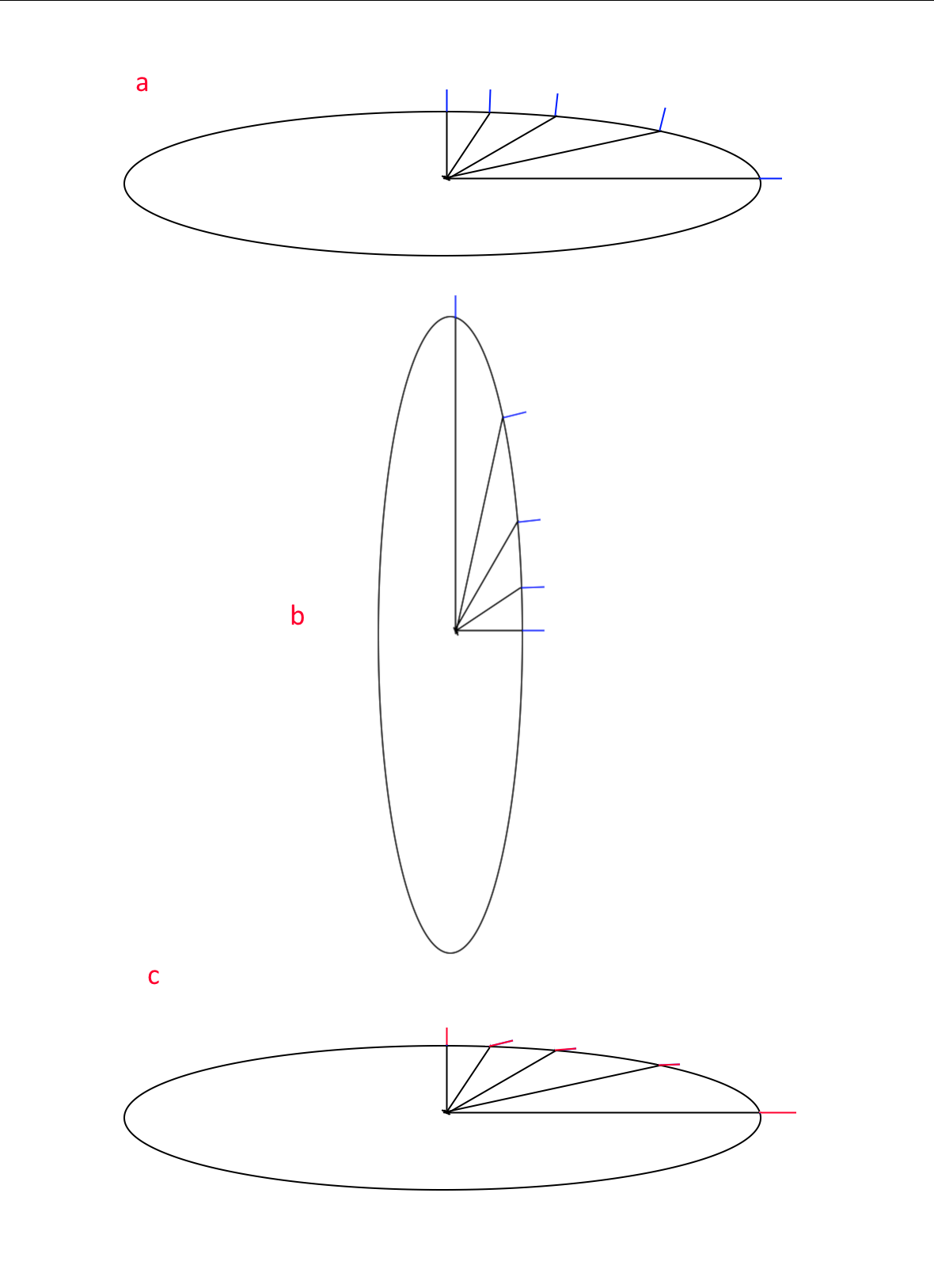 Oblate ellipsoid A with normals at collision position.
Oblate ellipsoid A with normals at collision position.


