This is a follow up to my previous thread: Realistic Emissive Color Rendering for Stars. I'd have just responded to that thread but it's locked. Surely I, the thread creator, should be able to respond to threads of my own creation only 2 months later? As a result, anyone coming across my previous thread will not benefit from this follow up.

To recap, I'm trying to determine how to accurately set the emissive color intensity for the sphere representing a star. The previous results didn't seem quite right.

I spent some time tinkering with the path tracing code and realized that I was calculating the intensity emitted by the star incorrectly for the “camera with optics” case. The correct way is to determine the emissive intensity of the star by dividing the power by the surface area, then scaling by a factor related to the BRDF (assuming Lambertian emission). This gives me the correct intensity when I sum the energy over all pixels in the image, regardless of the size of the star's sphere in the image.

These tables summarize the results of a few experiments:

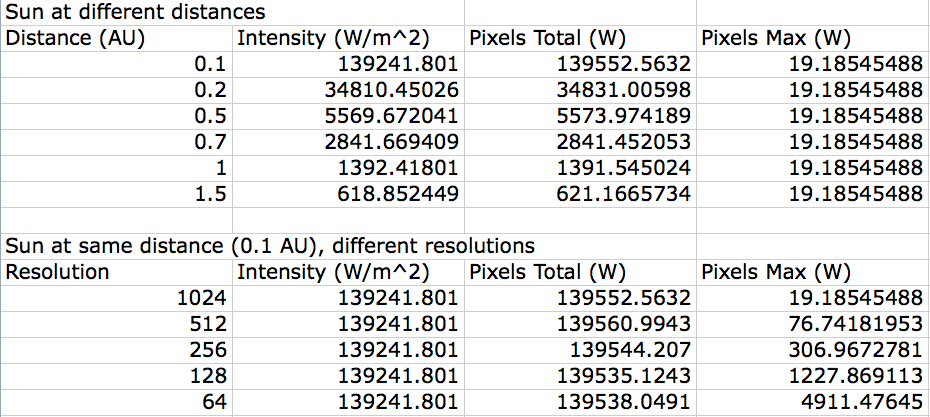
The first table compares the pixel intensities for a sun-like star (M=1.0 solar masses) at different distances from the camera. The camera has optics, 45 degree field of view, and a 1m^2 near plane (sensor) at a distance of 1 meter. You can see that the “Pixels Total” column is very close to the “Intensity” column which is calculated using the inverse square law. The errors vanish if I trace more rays per pixel. This verifies that the code is correct. The interesting bit is the “Pixels Max” column, which is the maximum pixel value in the image (of 1024x1024 pixels). The maximum pixel intensity is always the same, regardless of the star's distance.

The second table compares the pixel intensities for the same star at the same distance, but viewed with a different number of pixels on the sensor. Looking at the “Pixels Max” column, you can see that there is an inverse power relationship, where a halving of the resolution results in the maximum pixel intensity increasing by exactly a factor of 4.

So, from this we can conclude that the maximum brightness of the pixels of an emissive light source:

• Do not depend on distance from the light source
• Does depend on the light source's total power and radius.
• Also depends on the camera: the field of view, and sensor resolution (i.e. the angular pixel size).

If we compare the sun at 1 AU to a red dwarf with M=0.1 solar masses, with the red dwarf placed much closer so that the inverse square intensity is the same, we get these results:

M=0.1
Power: 3.67180264220761e23
Radius: 222052397.3021059
Distance: 4580890566.392502
Intensity: 1392.418010299886
TOTAL: 1395.720056778401
MAX: 0.179890714839311

M=1.0
Power: 3.916e26
Radius: 702191335.3752826
Distance: 149600000000
Intensity: 1392.418010299887
TOTAL: 1391.545024477073
MAX: 19.18545488292391

So, you can see that even though the total intensity in the image is the same, the intensity is spread out over more pixels in the case of the M=0.1 star, since it is much larger relative to the camera's field of view. This means that the M=0.1 star pixels would be more than 100 times less bright than the sun over all wavelengths (more than 6700 times less bright in visible light). Therefore, my original rendering in the original thread is definitely wrong. If the sun has emissive intensity of 9000, then the red dwarf is about 1.4, which is not even enough to saturate the tone mapper.

In summary, the emissive intensity of a star should be calculated using the following relation:

emissiveIntensity = starPower / (4.0*PI*starRadius*starRadius) / PI

This ignores the effects of the camera.

The fixed path tracing code is:

const Size resolution = 1024;
const Size samplesPerPixel = 1024;
const Float64 nearPlaneSize = 1.0;//0.02;
const Float64 nearPlaneArea = math::square( nearPlaneSize );
const Float64 nearPlaneDistance = 1.0*nearPlaneSize; // 45 degree FOV
const Float64 inverseSamplesPerPixel = 1.0 / samplesPerPixel;
const Float64 inverseResolution = 1.0 / resolution;
const Vector3d cameraPosition( 0.0, 0.0, 0.0 );
const Vector3d cameraDirection( 0.0, 0.0, -1.0 );
const Vector3d cameraUp( 0.0, 1.0, 0.0 );
const Vector3d cameraRight = math::cross( cameraDirection, cameraUp );
const Vector3d nearPlaneCenter = cameraPosition + cameraDirection*nearPlaneDistance;
const Float64 sphereSolarMass = 1.0;
const Float64 sphereTemperature = solarMassToTemperature( sphereSolarMass );
const Float64 spherePower = solarMassToLuminosityW( sphereSolarMass );
const Float64 sphereRadius = blackBodyRadius( sphereTemperature, spherePower );
const Vector3d spherePosition = 0.1 * Vector3d( 0.0, 0.0, -1.496e11 );// * math::sqrt( spherePower / solarMassToLuminosityW( 1.0 ) );
const Float64 sphereBRDFNormalize = 1.0 / math::pi<Float64>();

Random64 random( 123456789 );
Float64 maxPixelEnergy = 0.0;
Float64 totalPixelEnergy = 0.0;
ImageBuffer imageBuffer( PixelFormat::GRAY_8, resolution, resolution );
imageBuffer.allocate();

Console << "Power: " < spherePower;
Console << "Radius: " < sphereRadius;
Console << "Distance: " < spherePosition.getMagnitude();
Console << "Intensity: " < spherePower/(4.0*math::pi<Float64>()*spherePosition.getMagnitudeSquared());

for ( Index i = 0; i < resolution; i++ )
{
    const Float64 i01 = Float64(i)/resolution - 0.5;
    for ( Index j = 0; j < resolution; j++ )
    {
        const Float64 j01 = Float64(j)/resolution - 0.5;
        Float64 pixelEnergy = 0.0;
        
        for ( Index k = 0; k < samplesPerPixel; k++ )
        {
            const Vector2d sampleOffset( random.sample01<Float64>(), random.sample01<Float64>() );
            const Vector3d nearPoint = nearPlaneCenter +
                    (i01 + sampleOffset.y*inverseResolution)*cameraUp +
                    (j01 + sampleOffset.x*inverseResolution)*cameraRight;
            const Vector3d nearPointDirection = (nearPoint - cameraPosition).normalize();
            
        #if 1 // Ray casting (camera with optics)
            Ray3d ray( nearPoint, nearPointDirection );
            Float64 spherePointDistance;
            if ( !ray.intersectsSphere( spherePosition, sphereRadius, spherePointDistance ) )
                continue;
            
            const Vector3d spherePoint = nearPoint + spherePointDistance*nearPointDirection;
            const Vector3d sphereNormal = (spherePoint - spherePosition).normalize();
            // Points facing away from camera have 0 contribution.
            const Float64 sphereNormalDot = math::dot( nearPointDirection, sphereNormal );
            if ( sphereNormalDot > 0.0 )
                continue;
            
            const Float64 sphereSurfaceArea = 4.0*math::pi<Float64>() * math::square( sphereRadius );
            Float64 sampleEnergy = sphereBRDFNormalize * spherePower / sphereSurfaceArea *
                                    math::square(nearPlaneSize/nearPlaneDistance);
        #else // Sensor without optics
            const Vector3d sphereNormal = sampleSphereUniform( random.sample11<Float64>(), random.sample01<Float64>() );
            const Vector3d spherePoint = spherePosition + sphereRadius*sphereNormal;
            Vector3d spherePointDirection = spherePoint - nearPoint;
            const Float64 spherePointDistance = spherePointDirection.getMagnitude();
            spherePointDirection /= spherePointDistance;
            
            // Points facing away from camera have 0 contribution.
            const Float64 sphereNormalDot = math::dot( spherePointDirection, sphereNormal );
            if ( sphereNormalDot > 0.0 )
                continue;
            
            const Float64 distanceAttenuation = 1.0 / math::square( spherePointDistance );
            const Float64 sphereBRDF = sphereBRDFNormalize * (-sphereNormalDot);
            
            Float64 sampleEnergy = spherePower * sphereBRDF * distanceAttenuation;
        #endif
            
            pixelEnergy += sampleEnergy;
        }
        
        const Float64 pixelArea = (nearPlaneArea / (resolution*resolution));
        pixelEnergy *= inverseSamplesPerPixel * pixelArea;
        maxPixelEnergy = math::max( maxPixelEnergy, pixelEnergy );
        totalPixelEnergy += pixelEnergy;
        *imageBuffer( j, i ) = pixelEnergy;
    }
}

Console << "TOTAL: " < totalPixelEnergy;
Console << "MAX: " < maxPixelEnergy;

To follow up on the follow up, I have figured out how the camera parameters affect the intensity of pixels for a spherical emissive light source (star).

// When star is less than 1 pixel in size, pixel intensity is:
vec3 pixelColor = starPowerW / (4.0*PI*distance*distance);

//***************************************

// When star is more than 1 pixel in size, drawn as sphere:

// The intensity emitted per area on the star's surface. 
// Extra 1/PI is due to Lambertian radiation.
vec3 surfaceIntensity = starPowerW / (4.0*PI*PI*sphereRadius*sphereRadius);

// Determine pixel angular area.
// 4/PI accounts for square vs. round pixels (ratio of unit square to unit circle area).
float pixelAngularSize = fieldOfViewRadians / resolution;
float pixelAngularArea = pixelAngularSize * pixelAngularSize * (4.0/PI);

// Scale surface intensity by pixel area to get color.
vec3 pixelColor = surfaceIntensity * pixelAngularArea;

There are two different methods for drawing the star depending on its angular size. If it is smaller than 1 or 2 pixels in size, we draw it as a single point, which helps to avoid aliasing and flickering in intensity. The point's color intensity is just the standard inverse square law. For example, with a sun-like power of 3.9e26 watts, the inverse square law produces a pixel intensity of 1392 W/m^2 at a distance of 1 AU.

When the star is bigger on the screen than a few pixels, we use a sphere of realistic size to draw it. The above code shows how to determine the emissive color intensity of the sphere's surface based on the power, sphere radius, field of view, and resolution. The camera optics affect the intensity of the pixels. For instance, if we zoom in so that the star fills the whole screen, the brightness of the pixels is actually reduced, since the star's light is spread over more pixels in the image. If we zoom out, the star's light covers fewer pixels and therefore each pixel needs to be brighter so that we get the correct inverse square law intensity when summing the values for all pixels in the image.

The reason for this weird behavior is because in graphics the emissive lighting is treated as a constant value added to the pixel color in the pixel shader. This means to get physically correct results, so that the emissive surfaces match other surfaces in brightness, the emissive intensity needs to be scaled by the pixelAngularArea (in steradians).

Here is an example rendering of a sun-like star at 1 AU with the camera zoomed in so that it fills the image of size 1024px. The total value of all pixels in the image is close to 1392 W/m^2, just as it should be according to the inverse square law. The maximum pixel value is 0.001918 W/m^2/

Here is the same view, but rendered with a resolution of 128px. Like previously, the total value of all pixels in the image is 1392 W/m^2. However, since each pixel covers a larger angular area (64 times as much), the pixel intensity must be brighter (0.122778 W/m^2) to make the total 1392.

This all seems to make sense, but there is a question, that if we need to scale the emissive color to make the pixel intensities correct, shouldn't we also have to do the same for specular/diffuse lighting, since those are also affected by the camera's pixel size? Reducing pixel angular area (decreasing FOV or increasing resolution) means that the amount of light received by the camera is less. This seems to be a property of real cameras. I guess almost all games ignore this effect, since it would be weird for higher resolutions or smaller FOV to be darker (and therefore require brighter exposure/bigger aperture/higher ISO).