Hi,
I've been trying to convert my Euler rotations for animation to Quaternions, and I have finding myself in a situation where the behaviour and result is significantly different.
When applying Euler angles, I am having to negate all my rotations and then pass them to my rotation matrices and assemble the matrices as X *Y *Z where Z is multiplied first then Y and then X.
vec3 rotations = vec3(....)
rotations = -rotations;
auto rotation = Mat4::RotateX(rotations.x) * Mat4::RotateY(rotations.y) * Mat4::RotateZ(rotations.z);
auto offset_matrix = Mat::Translate(vec3(offset_from_parent.x, offset_from_parent.y, offset_from_parent.z));
global_matrix = parent_matrix * offset_matrix * rotation;This produces the correct result with rotation matrices and Euler angles:

I am trying to replicate these rotations but this time, using Quaternions.
I am doing the following:
vec3 rotations = vec3(....)
rotations = -rotations;
Quaternion rotX = Quaternion(rotations.x, vec3(1.0f, 0.0f, 0.0f));
Quaternion rotY = Quaternion(rotations.y, vec3(0.0f, 1.0f, 0.0f));
Quaternion rotZ = Quaternion(rotations.z, vec3(0.0f, 0.0f, 1.0f));
Quaternion concat = rotZ * rotY * rotX;
Mat4 quatRotMat = concat.ToRotationMatrix();
global_matrix = parent_matrix * offset_matrix * quatRotMat;However, the result is incredibly different and I am not able to understand why.
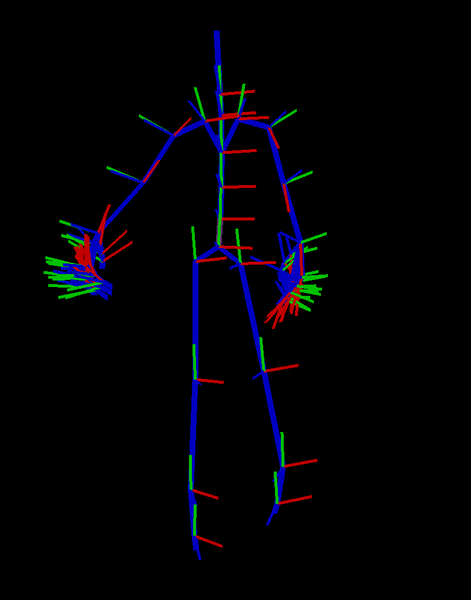
As I investigated further I found that, while Euler requires rotations to be negated, if I do not negate the rotations then the entire skeleton looks correct except the arms. The arms go in the air which seems like it might be simple fix of negating z, however negating z brings the arms down but they are still incorrectly placed.
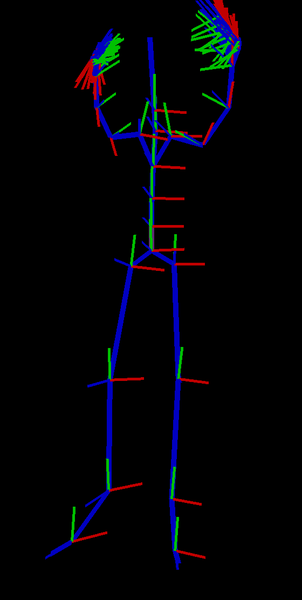
Negating the Z rotation angle, brings the arms down however, this has the arms down but they're moved back.
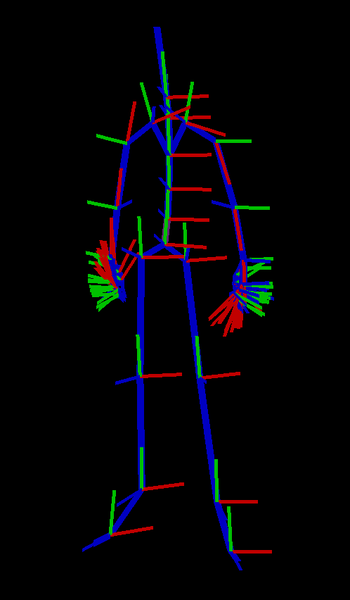
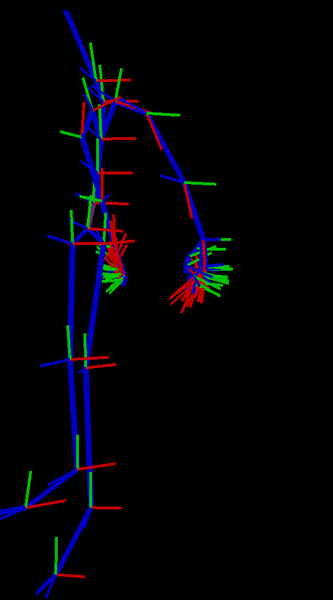
Wondering if anyones had a similar issue before and could provide some insight as to where I might be going wrong.
This is my Quaternion code:
Quaternion::Quaternion(float angle, const vec3& v)
{
float angleRadians = angle * M_PI / 180.0;
float rotAngle = angleRadians / 2.0f;
float cosAngle = std::cos(rotAngle);
float sinAngle = std::sin(rotAngle);
w = cosAngle;
x = v.x * sinAngle;
y = v.y * sinAngle;
z = v.z * sinAngle;
}
Mat4 Quaternion::ToRotationMatrix()
{
float x2 = x * x;
float y2 = y * y;
float z2 = z * z;
float xy = x * y;
float xz = x * z;
float yz = y * z;
float wx = w * x;
float wy = w * y;
float wz = w * z;
Mat4 ret = Matrix4::Identity();
ret.coordinates[0][0] = 1.0f - 2.0f * (y2 + z2);
ret.coordinates[1][0] = 2.0f * (xy - wz);
ret.coordinates[2][0] = 2.0f * (xz + wy);
ret.coordinates[3][0] = 0.0f;
ret.coordinates[0][1] = 2.0f * (xy + wz);
ret.coordinates[1][1] = 1.0f - 2.0f * (x2 + z2);
ret.coordinates[2][1] = 2.0f * (yz + wx);
ret.coordinates[3][1] = 0.0f;
ret.coordinates[0][2] = 2.0f * (xz + wy);
ret.coordinates[1][2] = 2.0f * (yz - wx);
ret.coordinates[2][2] = 1.0f - 2.0f * (x2 + y2);
ret.coordinates[3][2] = 0.0f;
ret.coordinates[0][3] = 0.0f;
ret.coordinates[1][3] = 0.0f;
ret.coordinates[2][3] = 0.0f;
ret.coordinates[3][3] = 1.0f;
return ret;
}
inline Quaternion operator*(const Quaternion& left, const Quaternion& right)
{
float w = (left.w * right.w) - (left.x * right.x) - (left.y * right.y) - (left.z * right.z);
float x = (left.x * right.w) + (left.w * right.x) + (left.y * right.z) - (left.z * right.y);
float y = (left.y * right.w) + (left.w * right.y) + (left.z * right.x) - (left.x * right.z);
float z = (left.z * right.w) + (left.w * right.z) + (left.x * right.y) - (left.y * right.x);
return {w, x, y, z};
}