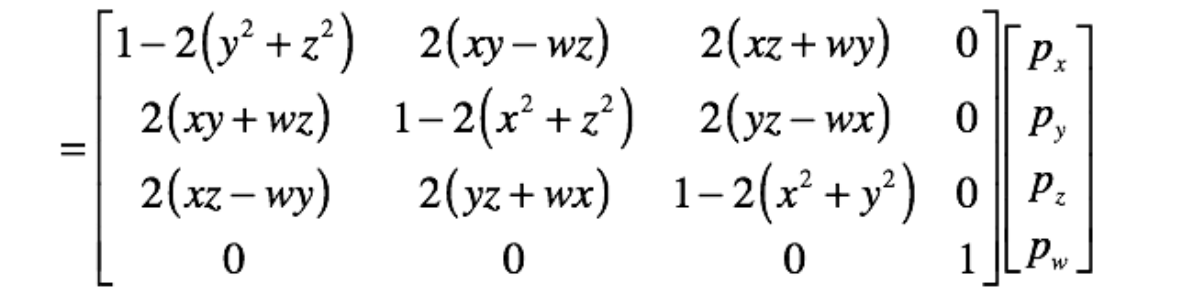I've been using Euler rotations for my animation for each joint an I am trying to understand how you would move away from Euler to Quaternions instead for animation since Euler can have issues.

Currently I am taking the rotations specified in degrees per angle for the joint and just multiplying the appropriate matrices from right to left to get the per frame per joint rotation for the animation.

Mat4 rotationMatrix = Mat4::RotateX(jointRot.x) * Mat4::RotateY(jointRot.y) * Mat4::RotateZ(jointRot.z);

To do the same rotation using Quaternions it would be the following?

This is what I am currently doing and my animation breaks, rotations seem incorrect

Quaternion RotX = Quaternion(jointRot.x, vec3(1.0f, 0.0f, 0.0f).unit());
Mat4 MatX = RotX.ToRotationMatrix();

Quaternion RotY = Quaternion(jointRot.y, vec3(0.0f, 1.0f, 0.0f));
Mat4 MatY = RotY.ToRotationMatrix();

Quaternion RotZ = Quaternion(jointRot.z, vec3(0.0f, 0.0f, 1.0f));
Mat4 MatZ = RotZ.ToRotationMatrix();

Mat4 rotationMatrix = MatX * MatY * MatZ;

// Quaternion
Quaternion::Quaternion(float angle, const vec3& v)
{
    float angleRadians = angle * M_PI / 180;
    float rotAngle = angleRadians / 2;

    float cosAngle = std::cos(rotAngle);
    float sinAngle = std::sin(rotAngle);

    w = cosAngle;
    x = v.x * sinAngle;
    y = v.y * sinAngle;
    z = v.z * sinAngle;
}

// To matrix function:
Mat4 Quaternion::ToRotationMatrix()
{
    float x2 = x * x;
    float y2 = y * y;
    float z2 = z * z;
    float xy = x * y;
    float xz = x * z;
    float yz = y * z;
    float wx = w * x;
    float wy = w * y;
    float wz = w * z;

    Mat4 ret;

    ret.m[0][0] = 1.0f - 2.0f * (y2 + z2);
    ret.m[1][0] = 2.0f * (xy - wz);
    ret.m[2][0] = 2.0f * (xz + wy);
    ret.m[3][0] = 0.0f;

    ret.m[0][1] = 2.0f * (xy + wz);
    ret.m[1][1] = 1.0f - 2.0f * (x2 + z2);
    ret.m[2][1] = 2.0f * (yz + wx);
    ret.m[3][1] = 0.0f;

    ret.m[0][2] = 2.0f * (xz + wy);
    ret.m[1][2] = 2.0f * (yz - wx);
    ret.m[2][2] = 1.0f - 2.0f * (x2 + y2);
    ret.m[3][2] = 0.0f;

    ret.m[0][3] = 0.0f;
    ret.m[1][3] = 0.0f;
    ret.m[2][3] = 0.0f;
    ret.m[3][3] = 1.0f;

    return ret;
}

snoken said:
float angleRadians = angle * M_PI / 180;

I guess it does not work because your function takes angles in degrees, not radians. Or do your matrix functions also take degrees?

Ideally all your functions should take radians, and you do all your math with radians. Degrees are again only useful for human interface reasons. (I never understood why OpenGL used degrees for rotations)

Otherwise your code should work in principle.

Thanks for the reply! My Euler rotation matrices also took angles in degrees and converted to radians which worked.

hmm, then my guess is Quaternion::ToRotationMatrix(). Do you use this code elsewhere, knowing it works?
I've compared it with my code, and it seemed the row column indices are reversed.

Try to swap it for all the lines filling the matrix, so

ret.m[1][2] = 2.0f * (yz - wx);

becomes

ret.m[2][1] = 2.0f * (yz - wx);

I'm not sure, but worth a try.

Thanks for the reply! my matrices use indexing as col, row

Have you tried switching the order in which the X, Y, and Z matrices are multiplied? There are 6 different orderings which produce different results. The ordering would have to match whatever system is generating the animation data. This is another reason why Euler angles are not preferred, due to the ambiguity.

Thanks for the reply! When doing Euler I was using:

auto per_frame_joint_rot = Mat4::RotateX(rotation.x) * Mat4::RotateY(rotation.y) * Mat4::RotateZ(rotatin.z);

I'm following the same for my Quaternions I believe

No idea about the details, but for debugging it helps if you take very small steps. Have just 1 element as input to rotate. Checks what happens when all axes rotate 0 degrees. Then try a known rotation for just 1 axis at a time, for all 3 axes separately (3 experiments thus). You may also want to try different amount of rotation. Then start combining rotations, change the initial position of the input element, and so on.

When the smaller experiments work you're building confidence in correctness. If it fails, you have a smaller testcase to debug to find the root cause.

You could write these as unit tests.

snoken said:
Thanks for the reply! my matrices use indexing as col, row

Well, tbh i'm not even sure anymore which is called column and which row.
I assumed ‘rows’ 0-2 give us the orientation basis vectors, and the 3th row gives translation vector. ‘Columns’ then index x,y,z,w of the vectors.
But seems i'm wrong, and it's actually called the other way around. Columns give basis vectors, and rows index dimensions.

However, here is the code i'm using:

class Matrix3
{
    Vector3 mCol0; // x basis vector
    Vector3 mCol1; // y
    Vector3 mCol2; // z
    // ...
}
inline Matrix3::Matrix3( const Quat & unitQuat )
{
    float qx, qy, qz, qw, qx2, qy2, qz2, qxqx2, qyqy2, qzqz2, qxqy2, qyqz2, qzqw2, qxqz2, qyqw2, qxqw2;
    qx = unitQuat.getX();
    qy = unitQuat.getY();
    qz = unitQuat.getZ();
    qw = unitQuat.getW();
    qx2 = ( qx + qx );
    qy2 = ( qy + qy );
    qz2 = ( qz + qz );
    qxqx2 = ( qx * qx2 );
    qxqy2 = ( qx * qy2 );
    qxqz2 = ( qx * qz2 );
    qxqw2 = ( qw * qx2 );
    qyqy2 = ( qy * qy2 );
    qyqz2 = ( qy * qz2 );
    qyqw2 = ( qw * qy2 );
    qzqz2 = ( qz * qz2 );
    qzqw2 = ( qw * qz2 );
    mCol0 = Vector3( ( ( 1.0f - qyqy2 ) - qzqz2 ), ( qxqy2 + qzqw2 ), ( qxqz2 - qyqw2 ) );
    mCol1 = Vector3( ( qxqy2 - qzqw2 ), ( ( 1.0f - qxqx2 ) - qzqz2 ), ( qyqz2 + qxqw2 ) );
    mCol2 = Vector3( ( qxqz2 + qyqw2 ), ( qyqz2 - qxqw2 ), ( ( 1.0f - qxqx2 ) - qyqy2 ) );
}

This comes from Sonys old Vectormath library, which someone has maintained here: https://github.com/glampert/vectormath/tree/master

They call the basis vectors columns as we see. But no matter how we call it, you can compare it has the same math as yours, but the final row / column indices are swapped. And because we both follow the OpenGL matrix convention, we should have the same code.

So if you have it wrong, maybe because looking up example code from somebody who used the other convention, you would actually get the transpose of the intended matrix. That's still a rotation, just the wrong way around. But since it's a valid rotation the bug can remain undetected for some time eventually.

Have you tried to swap the indexing?

Thanks for the reply. My matrix indexes as col, then row so index [0][1] would read column 0, row 1. To convert a quaternion to a rotation matrix, I am using the following: