I've been tinkering with my game engine for some time now (feels like nearly 20 years) and a few years ago I implemented PBR with Image Based Lighting. I was kind of happy with it for a while but something really bugged me with the specular highlights. I put it aside whilst I worked on other things like animation and material creation (I'll follow this topic up with some posts on that).
The other day, I'd had enough, I wasn't happy with my specular highlights so I set about trying to understand the math behind the BRDF calculations. A night spent with ChatGPT had armed me with a lot more understanding of the different components involved and this helped me to figure out what it was that was irritating me.
A few years ago, I tinkered with the material system in Unreal 4 and if you have a simple sphere with a shiny plain material, the specular highlight, when seen at glancing angles looked wrong to me, it was circular instead of wrapping itself around the curve of the sphere. I did make a post about this back in 2015 (https://gamedev.net/forums/topic/670910-pbr-specular-brdf/?page=1).
I think it was done this way in order to help with the specular reflections at grazing angles, i.e. to give that long specular reflection you see with car lights on a wet road or the sun setting low over the sea. Either way, both looked wrong.
What I found with the BRDF I was using (which was fairly standard I think), was that the Distribution function was using the surface normal dotted with the half vector as its input. Having spent a few hours trying to draw pictures and visualise the various vectors in my head, this didn't seem physically right. So I changed mine to what I thought seemed more physically plausible which was to use a reflection vector from the incident (eye vec) about the normal and to dot that with the light. What this actually gave me was exactly what I was looking for, this:

..rather than this (using half vector):

I thought maybe this was just my implementation but when I checked Unreal 4, it looked like it was using the half vector too in its implementation as it also had this circular, non curved lobe.
This was all well and good, but I ended up with terrible problems when the sun was at glancing angles on a flat surface. The specular lobe would grow and shrink and give really inaccurate results:

I believe this had to do with the fact that the numerator for the BRDF algorithm is essentially D x G x F and whilst the Distribution function was fine:

Multiplying in the Fresnel was essentially causing the specular lobe to get bigger at glancing angles. What I really wanted was a consistent lobe at any angle regardless of Fresnel, but that meant taking out the Fresnel calc (and adding it later). From examining the various components of the BRDF, I knew that the Fresnel term basically gives something like this:


And I could see that this would just increase the Normal Distribution Function result for the specular lobe. What's not easy to see is that the black area at the centre of the sphere, i.e. at viewing angles close to the surface normal, is not 0, it's something like 0.04 or whatever the constant is, typical Fresnel values. So what about if I just multiply the D and G terms by the constant 0.04, which brings my specular lobe to this (this is essentially returning D x G x 0.04):


So then I realised I can't not have any Fresnel so I started looking at where I could add it in. The denominator component (4 * dot(normal, incident) * dot(normal, light)) was something I played with but didn't look right. I then took it out completely and just added my fresnel in using 1 + F whilst calculating the indirectDiffuse (or just diffuse for non-IBL):


Not looking too bad and when I switch on IBL:


Also looking pretty good. So what about the glancing angle with bumpy material long trail effect that I've longed for and never got:




So what about with roughness added, this is where it could all fall apart without the energy conservation part of the equation:

Looks pretty good to my eyes.
So what I essentially now got it this:
specular = D * G * 0.04f;
ambient = pow(lerp(ambientFinalColour, lightColour, saturate(NdotL)) * (1 + F), 2.2);
indirectDiffuse = (irradianceColour * Albedo * Ambient * fullyLit * (1 + F)) + (irradianceColour * Albedo * shadowColour * (1 - fullyLit));
So I've added the Fresnel term into the ambient and indirect diffuse colours. I'm ignoring the fact that I've essentially multiplied in the straight on Fresnel term (0.04) and then also added it to the diffuse because the difference is negligible. The good thing about this is that it's going to be faster as you don't have those extra calcs in the denominator.
I can also add in a light intensity variable too, just to increase the size of the specular highlight without causing any issues (seen here with IBL on):

Be interested to hear what you think and if you can try this in your engines to see if you get comparable results.
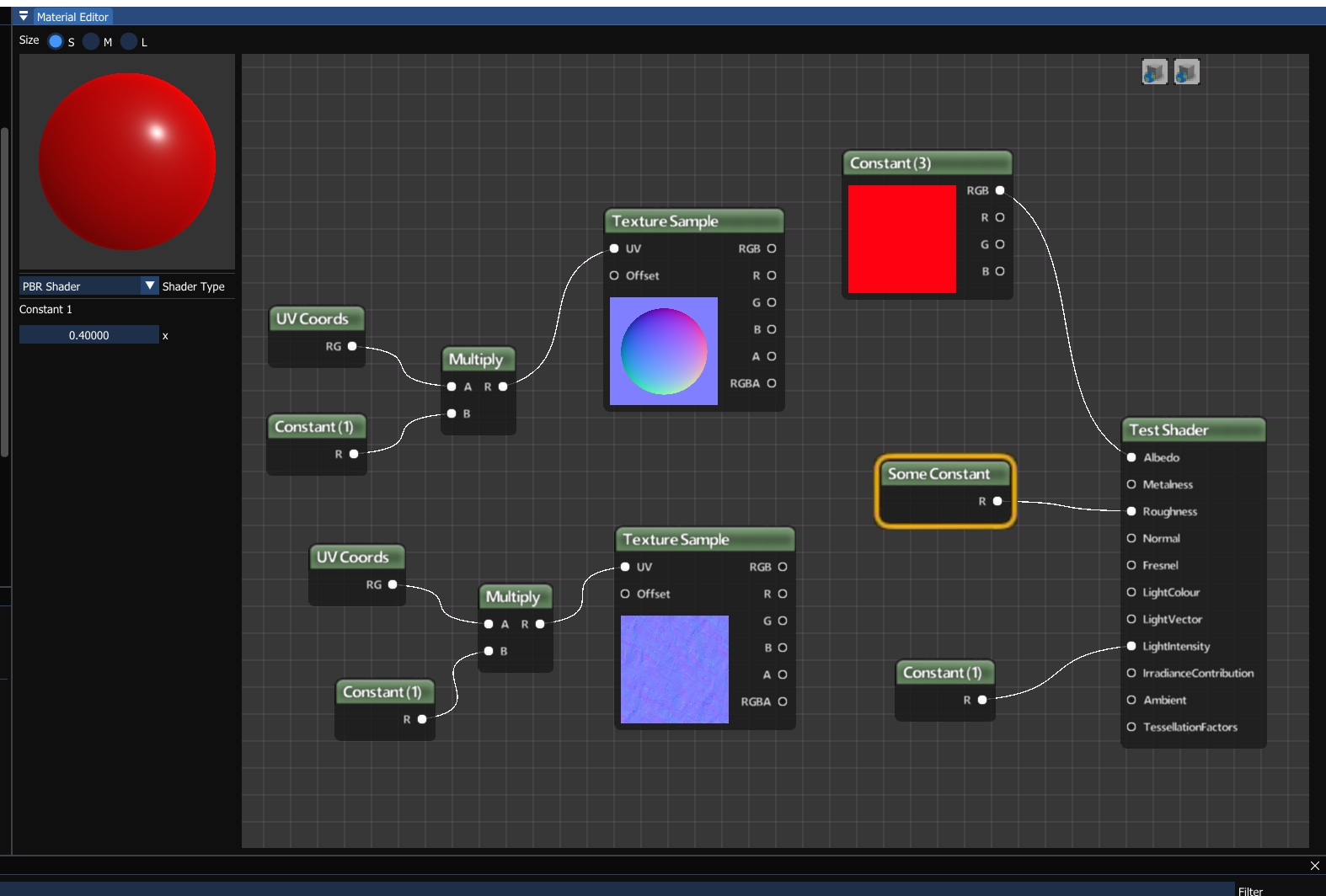
I'll be sharing a video on my material editor soon too, just to showcase it (excuse the shameful copy of a certain well-known editor's textures…, I'll change these at some point):
Edit: I realise I haven't got my environment map for IBL sync'd up with the atmosphere - I was just trying out a new cheap scattering technique I found on ShaderToy ?

















