I'm sure there is a name for this sort of problem / algorithm but I can't seen to get anything useful off google.

Imagine you have an infinite grid, and you are generating a path along cells in the grid one cell at a time. Each cell (other than the first) has one side that is an entrance, and another side that is an exit. There is no branching.

For example, this is a finite grid where there is no dead end:

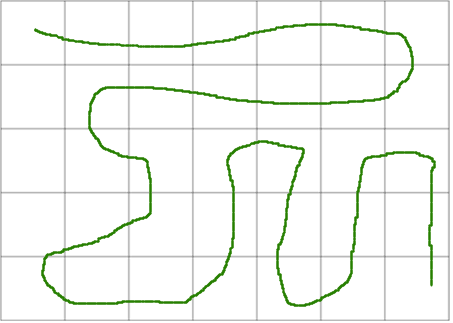
And here is one where the is an obvious inevitable dead end:

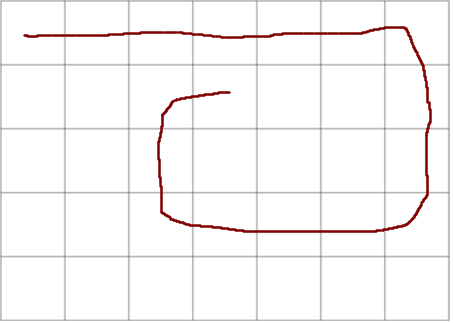
I'm looking for any sort of algorithm that would help be build this one cell at a time.

Ideally it could be implemented as a function that I provide a list of all cells in the current path, and it provides 1-3 directions that guarantee there will be no dead end.

The generated path does not have any constraints, I don't care if it is dense or sparse, as long as it can keep generating one cell at a time.

One idea I had was creating a “bounding shape” that contains all cells of the existing path, and not permitting generating in that. Maybe using some sort of string pulling algorithm to build the shape.

I'm open to any other suggestions.

Thanks

I haven't thought about this carefully, but it seems like you run into a dead end if and only if the path contains two adjacent segments going in the same direction.

Edit: It's not quite that simple, because you can isolate a region by having two corners that touch at a point, without sharing an edge. But I think a rule of this type could work, with some adjustments.

There are patterns like the Hilbert Curve ( https://en.wikipedia.org/wiki/Hilbert_curve​ ) that recursively apply on themselves.

Not sure if it works for you, but it may be useful to read a bit about it.

There's definitely some merit in recursive solutions, fractals, and similar approaches.

However, I would be tempted approach this as a simpler 2-level problem: a ‘coarse’ grid that is trivially trivially guaranteed to be able to expand infinitely - for example, a spiral, and each cell of that grid being itself subdivided into another grid cells (e.g. 10x10) which you path across like the above examples.

You can use any system you like to path across the ‘inner’ grid, and because these grids are smaller, you can use brute force to check validity, which isn't feasible on a single infinitely-sized grid. However, I'd consider something simpler, such as generating the shortest path from the entry node to the exit node and then attemping a random set of ‘rewrites’ of path sections to make the path more interesting.

e.g. This 3x3 section of the grid, including 3 steps of the existing path:

. . .
1 2 3
. . .

Can be safely transformed into the following:

2 3 .
1 4 7
. 5 6

Because the start and end positions remain unchanged, and only unused spaces were added to the path.

The main theme is - start with something guaranteed to extend infinitely, and then apply transformations to it that do not violate the guarantees.

Reminds me on this paper: https://cs.wellesley.edu/~pmwh/papers-fcpcg/FDG2021-Mawhorter-fractal-author.pdf​

Which i saw on this blog: https://www.boristhebrave.com/2023/01/28/infinite-quadtrees-fractal-coordinates/​