I've been stuck on a problem for a long time and wondered if anyone could help tell me where I'm going wrong.
I have multiple objects in world space, each object has multiple snap points.


In the image the yellow object is fixed and already inserted, the grey object is "inserting" and movable by mouse until clicked, which then inserts. The objects snap point is under the cursor, and you can cycle through the snap points by pressing Ctrl, similar to CAD software.
The snap points are defined by their own coordinate frame.
I'm using the following method to find the rotation matrix between any 2 snap points:
https://web.archive.org/web/20200223130502/http://www.meshola.com:80/Articles/converting-between-coordinate-systems
When the yellow object has no rotation (Euler 0,0,0), it works perfectly for all snap points (as shown in the images above).
However when the yellow object has an arbitrary rotation, only 1 out of 4 snap points work on the grey object (Images below).
The snap point that works is when the coordinate frame of the Grey obj snap point is inline with the world frame, with negative direction.
Unit vectors of snap point coordinate frame (grey obj):
X = -1, 0, 0
Y = 0, -1, 0
Z = 0, 0, -1

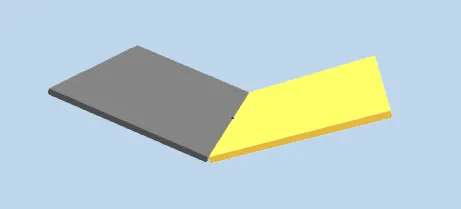
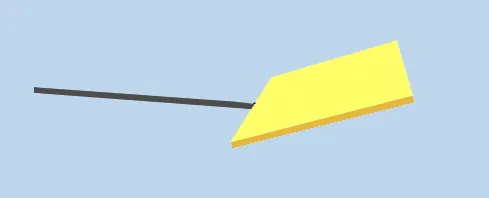

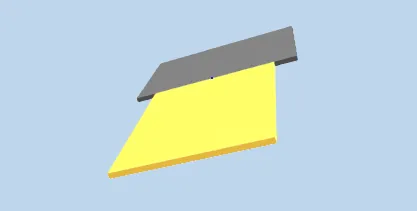
The only time it works is when the Grey object active snap point has the coordinate frame defined above.
I'm hoping someone can point out what I'm doing wrong without having to read my code, but I can share code if needed, it's in VB though







