Hi

I have been using Bezier and convex hull libraries (C#) to try and make smooth border around rectangles and I'm trying use Quadratic bezier curves but the problem is I don't know how to calculate the middle control point.

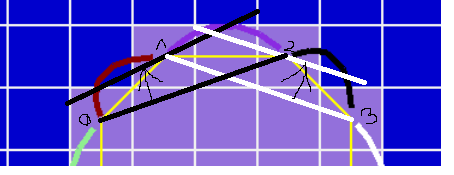
Here's a screenshot of what I got so far (yellow line is convex hull, curves are the bezier):

And here's the attemp to calculate that middle control point (ax,ay)

(sp is start point and ep end point)

                double angle = Math.Atan2(((double)(ep.Y - sp.Y)),((double)(ep.X - sp.X))); // Count the direction from start point to end point


                angle += Math.PI - (Math.PI * 0.25);

                double length = 75.0;

                int ax =  (int)((Math.Sin(angle) * length));
                int ay = -(int)((Math.Cos(angle) * length));

                
                Bezier bez = new Bezier(new Vector2(sp.X, sp.Y), new Vector2(((sp.X + ax) ) , ((sp.Y + ay) ) ), new Vector2(ep.X, ep.Y));

Any tips are welcome but hopefully not heavy math formulas because I don't often understand those

thx!

heh65532 said:
I don't know how to calculate the control point

I've never seen calculating the control point. That may be a thing but I've only seen calculating the curve from the control points, not vice-versa.

Also, cubic bezier curves are way more common and versatile without much (if any) added complexity.

https://www.jasondavies.com/animated-bezier/​

The second one at that link is Quad, the 3rd is Cubic. With cubic graphical representation, the line going between the 2 center points is usually omitted and those 2 points are called handles.

I just noticed a link on that page. It looks really good. I will have to check it out myself.
https://pomax.github.io/​

fleabay said:

heh65532 said:
I don't know how to calculate the control point

I've never seen calculating the control point. That may be a thing but I've only seen calculating the curve from the control points, not vice-versa.

yes that's the goal, to calculate the curve but I don't know where to get those control points…

@heh65532 I updated my post. Check the links to see if that answers any of your questions.

The control points are the start of the curve, the end of the curve and 1 or 2 points (depending on quad/cubic) to deform/shape the curve.

fleabay said:

@heh65532 I updated my post. Check the links to see if that answers any of your questions.

The control points are the start of the curve, the end of the curve and 1 or 2 points (depending on quad/cubic) to deform/shape the curve.

I may have used wrong terms then cause I'm such a noob for these things. what I meant was to figure the middle control point (passed in Bezier() as second parameter)

You can put the middle control point right between the other 2 points. It'll be a straight curve (line) until you move it.

fleabay said:

You can put the middle control point right between the other 2 points. It'll be a straight curve (line) until you move it.

I'm not moving it manually, this is an attempt to render smooth lines around the tiles. so not user interactable

@heh65532 Ah yes. I should have read your first post better.

I've never implemented that before and I'm not qualified to offer any solutions.

Unless someone else give you specific info, you can start with googling something like “create a circle from bezier curves” and see that it's not a problem with a cut and dry solution.

IMHO, you should use Catmull-Rom curves instead of Bézier curves. The main reason why is that the Catmull-Rom curve has greater continuity when compared to Bézier curves. Just my 2 cents.

heh65532 said:
I have been using Bezier and convex hull libraries (C#) to try and make smooth border around rectangles and I'm trying use Quadratic bezier curves but the problem is I don't know how to calculate the middle control point.

Stoping here, ignoring the following conversation.

Actually i don't see a need for trig to calculate the middle control point. Here's the trivial (and only?) way to do this:

We want to calculate the middle CP for the top segment between points 1 and 2.

To do so, we take the line from 0 to 2 and transport it to point 1, which defines our tangent direction at this point. (black drawn lines)

We do the same for the line 1 to 3, defining tangent intersection for 2. (white lines)

Then we calculate the intersection for those two transported lines, giving us the middle CP we want.

Noitice: This only works in 2D, because in 3D lines do not necessarily intersect.
And even in 2D it breaks if the intersection flips to the wrong side (causing sharp, not smooth spikes in the curve), or if our tangents re parallel and have a intersaction at infinite distance.

That's why quadratic bezier splines are rarely used, and people instead use cubic beziersplines with 4 control points not just 3.
With 4 control points, you can define tangents independent from adjacent control points, so none of those problems exist. Additionally we gain more control over the tension of the curve.

Another commonly used curve type is Catmull Rom splines, whiche are nice becasue you do not have to worry about tangent directions at all.
However, with Catmull Rom splines (lacking any extension to model tension), the curvature focuses at the control points. They look sharp and angled, while the segments between them look smooth and straight.

You'd need to lookup some examples showing results, but in general i'd recommend cubic bezier if visuals matter.

Splines are not the only way to smooth out a grid. Am cubic texture filter (taking 3x3 samples not just 2x2) also generates smooth results, for example.