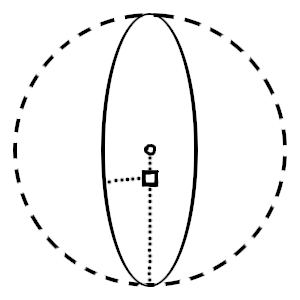
I'm currently trying--as part of implementing a new feature--to find the point on a squashed circle that is nearest to the player's location.

The circle in question is squashed simply by the application of a scalar applied to its x-axis.

I already have code that can determine the nearest point on an unsquashed circle, I do believe. And it seems to me that there should be a relationship between this point and the equivalent point on the squashed version.

Now, I can't just scale the x-coordinate of the nearest point on the unsquashed-circle--that results in a point that slips towards the vertical ends of the squashed circle.

However, it seems to me that the correct point might be found by taking the vector between the centre of the circle and the closest point on the unsquashed circle, and reducing it. That is, that vector should pass through both the unsquashed and the squashed circle, and I think that the point at which it passes through the squashed circle is the point that I want. The vector to the point on the squashed circle should be shorter in general than the vector on the unsquashed circle, and so it should be just a matter of reducing the vector on the unsquashed circle by the appropriate amount.

And here, then, is the point at which I'm finding myself stuck: I don't know by how much to reduce the vector.

When the closest point lies on the x-axis, the reduction should be, I believe: circle_radius * (1 - squashingScalar). And naturally, when the closest point lies on the y-axis, the reduction should be zero.

But as to how it varies in-between… I don't know.

I've tried a few options, in particular the use of sine (specifically, 1 - sin(angleOfVector) * (1 - squashingScalar), and some variations). This produces the correct results for the point lying on the x-axis and the point lying on the y-axis--but not in-between.

Being stumped, I thus come here for suggestions--does anyone know the proper reduction of the vector in question?

Thaumaturge said:
I already have code that can determine the nearest point on an unsquashed circle, I do believe. And it seems to me that there should be a relationship between this point and the equivalent point on the squashed version.

Stopped reading here. It sounds you seek for a closed form solution to find the closest point on an ellipse?
Afaik that's a no. You need iterations to find a good enough approximation.
Problem is hard enough for a lengthy paper: https://www.geometrictools.com/Documentation/DistancePointEllipseEllipsoid.pdf

Your idea would work for example if the problem would be ‘find intersection of a ray with an ellipse’.
Then you could transform the ellipse to become a circle, apply the same transform the the ray, find intersection and untransform.

Never thought about the problem. The PDF is from Eberly so that will probably get you the best mathematical result.

If you want something simpler, that's not 100% accurate, you can maybe cut the ellipse into circles that are contained inside the ellipse. They would get smaller as they reach the edge where the ellipse comes towards a peak. Maybe come up with something there and see how well it works. Although I guess you could just find the closest quadrant of the ellipse to the point, and then interpolate in some steps over that ¼ of the ellipse and checking the distance from point to point.

JoeJ said:
. It sounds you seek for a closed form solution to find the closest point on an ellipse?

Hmm… I'm honestly not sure of my definitions here: my impression, at least, is that an “ellipse” is a more-general shape than what I have.

To be clear, my “squashed circle” implementation has no concepts of dual focal points, etc. It's literally just a circle with a scalar applied to the x-axis.

Thus it may be that a general solution of ellipses might well be more complex than for my specific case--perhaps, at least!

And intuitively, looking at a diagram of the case that I'm working with, it does seem like there should be some consistent relationship between the length of the vector from the circle's origin to the closest point on each of the squashed and unsquashed versions of the same circle…

JoeJ said:
Your idea would work for example if the problem would be ‘find intersection of a ray with an ellipse’. Then you could transform the ellipse to become a circle, apply the same transform the the ray, find intersection and untransform.

Hmm… Something like that might work, as it is essentially what I'm doing. I might have to experiment with scaling the x-coordinate of the line that I'm intersecting with the unsquashed circle by the inverse of the squashing-factor that I'm applying…

dpadam450 said:
If you want something simpler, that's not 100% accurate, you can maybe cut the ellipse into circles that are contained inside the ellipse

Honestly, even that is likely more complex than I'm inclined to for this feature!

Nevertheless, thank you for the suggestions! It does sound like an interesting approach!

About approximations, Inigo Quilez has worked out some methods, spread over multiple articles on his website iirc.

I might have to experiment with scaling the x-coordinate of the line that I'm intersecting with the unsquashed circle by the inverse of the squashing-factor that I'm applying…

Yes. If you want to intersect ellipse with a line, this works.

All right, a variation on the above seems to have worked!

Or at least, worked within tolerance: there are some oddities, but they're acceptable for my purposes, I feel.

To be specific, I tried scaling the x-coordinate of the player's location by the inverse of the circle's “squashing factor”. This seemed to work--but only when the player's position lay on the squashed circle. Away from that, it was off.

And indeed, I can see why that is, I believe. Consider the following case:

Here the solid line shows the squashed circle, the dashed line shows the unsquashed circle, the small circle shows the origin, and the square shows the player's position.

Here, the player's x-coordinate is pretty much zero. As a result, scaling will result in a similarly pretty-much-zero value--and a resulting vector that still points pretty much towards the bottom of the circle.

However, as the diagram shows, the player's position is actually closer to a point near the middle of the circle.

It seems to me, then, that what's called for is less a scaling than an offset.

Specifically, I'm now offsetting the player's x-coordinate by the difference between the x-width of the unsquashed and squashed circles, in the direction indicated by the player's x-coordinate.

Now, this becomes problematic when the player is positioned beyond the top or bottom of the circle, as the circle, squashed or unsquashed, has no “x-width” there. In that case, I'm falling back on simply scaling the x-coordinate of the player's position.

That fallback results in some jumping around of the calculated “nearest point” under certain circumstances--but I think that it should be fairly unproblematic.

Of course, if anyone has a better idea, I'm open to it! But for now, I think that this works! ^_^

With my thanks to those who replied in this thread! ^_^

As I recall the ellipsoid version of player bounding collision, works by scaling everything in one axis to get a sphere and squished geometry, doing your calculations using sweep sphere, and then scaling back the collision data. I would assume this would also give the correct answer for what you need.

Edit: To be clear I'm not 100% sure of that. It's just seems kind of intuitive since the collision works.

Hmm, the descriptions are just too confusing. : )

From looking at the picture i would say: The intersection of the line from the center through the square can be found, no matter where the square is, because we have line.
But the closest point on the ellipse to the square can not be found (without a search), because we don't know the direction towards the closest point.

I had this problem quite often. It usually means we can find the collision along the velocity (our direction) with an ellipse, but if our point is already inside the ellipse and we want to move it out to the closest point on the surface, we're fucked.

Once i did cloth collision against character skin, and i modeled the skin with capsules per vertex, oriented and squashed along the normal. The squashing reduced the bumps i would get from using spherical caps.
If cloth vertices went inside, i have projected them out along the normal. Which is wrong, and caused jitter, but it worked well enough. Doing iterations for each collision would be too expensive.

Another example was the limit of a ragdoll joint. Obviously, a simple model would be a cone with a elliptical, not circular base, because we can not move our limps for the same angle at any orientation.
But to avoid the ellipse, i replaced it with the cross section of a capsule, which is a similar shape composed of arcs and lines. And i got this, where the limit is made from 4 cones (white lines):

And i don't regret this, because now i also can solve IK problems with closed form analytical solutions.

So maybe you can do the same, using such shape:

Finding the closest points is easy, although the code becomes more branchy and covers more cases.

Otherwise, if you don't do this so often per frame, a proper iterative solution is probably the best choice.

JoeJ said:
Hmm, the descriptions are just too confusing. : )

Ah, my apologies!

Let me try again, if I may:

As you can see in the diagram, I have a vector running from the centre of the circle to the player's position.

Since the squashed form of the circle is simply the circle with a scaling factor applied, one might think that the closest point on a squashed circle might be found by similarly scaling the player's position. However, as the diagram shows, this doesn't work.

However, there is still a geometric relationship here, I do think. But it's one not of scaling the player-position, but of moving it.

Specifically, what seems to work is this, if I recall correctly:

• Find the width of the circle at the player's y-position.
• Find the width of the squashed circle at the same y-position
• Calculate the difference between the two
  • That is, figure out how far the perimeter of the squashed circle is from the perimeter of the unsquashed circle at this point.
• Then shift the player's position by that amount in the appropriate direction along the x-axis
  • The “appropriate direction” being simply the x-axis direction in which the player-position already lies--i.e. if the player-position has an x-coordinate of -0.4, move the position in the negative direction along the x-axis.
• Calculate the closest point on the unsquashed circle from this new, offset position
• And finally, squash the result--i.e. scale it on the x-axis.

Now, this does rely on being able to calculate the width of the two forms of the circle--which is undefined beyond the y-extent of the circle. That's the point at which I switch back to simple scaling.

JoeJ said:
But the closest point on the ellipse to the square can not be found (without a search), because we don't know the direction towards the closest point.

And yet, what I have does seem to work. :P

(At least, within the bounds described. And I suspect that there's a solution outside of those bounds--I just haven't spent too much time and energy looking for it.)

Gnollrunner said:
As I recall the ellipsoid version of player bounding collision, works by scaling everything in one axis to get a sphere and squished geometry, doing your calculations using sweep sphere, and then scaling back the collision data. I would assume this would also give the correct answer for what you need.

Hmm… That's indeed close to what I've ended up doing, as described above, I believe--save that I've found that simple scaling doesn't seem to quite work.

(And that I'm only checking a single point against the circle, so no sweeping is called for, I daresay.)

[edit] Unintentional double-post--my apologies!