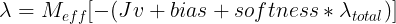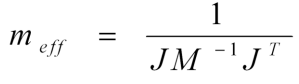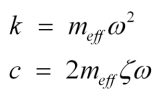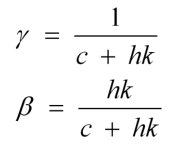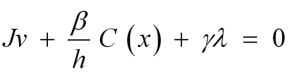I'm trying to constraint an object's vertical position to a certain height using soft constraints. This means it will behave like a spring. The constraints are solved using a sequential impulse solver. I'm using the technique shown in Eric Catto's Soft Constraints talk and Ming-Lun Chou's Soft Constraints video shown at the links below.

https://box2d.org/files/ErinCatto_SoftConstraints_GDC2011.pdf​

https://www.youtube.com/watch?v=UUt4Lko2wFI

I'm having two problems. First, during the loop which solves the constraint iteratively, the result is different depending on the number of iterations.

5 iterations

20 iterations

As you can see, the box stops oscillating faster when there are more iterations. The number of iterations should not be affecting the box like this.

The second problem I'm having is that when I set zeta to 0 the box stops oscillating over time like in the above gifs. This should not happen as shown in Erin Catto's paper linked above:

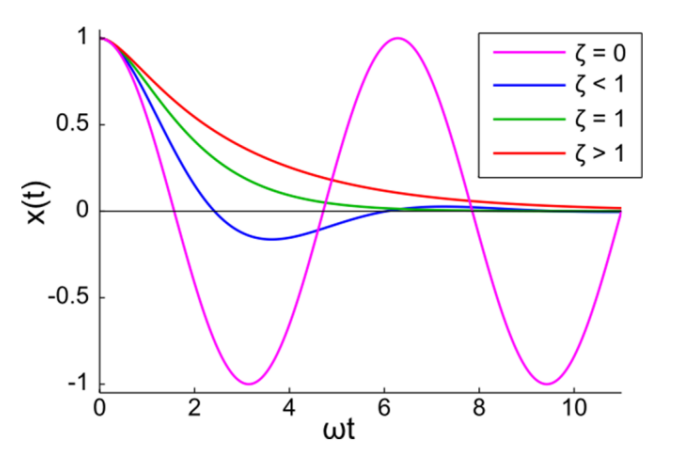
As you can see, when zeta is 0, the box should oscillate forever and not come to rest. In both examples above, zeta is set to 0 and omega is set to 2 times pi.

Here is my implementation.

// Integrate
rigid_body.velocity.y += acceleration * delta_time;
transform.position.y += rigid_body.velocity.y * delta_time;

// Calculate constants
let d = 2.0 * rigid_body.mass * SPRING_ZETA * SPRING_OMEGA;
let k = rigid_body.mass * SPRING_OMEGA * SPRING_OMEGA;

let gamma = 1.0 / (d + delta_time * k);
let effective_mass = (1.0 / rigid_body.mass) + gamma / delta_time;

let beta = (delta_time * k) / (d + delta_time * k);
let pos_error = 3.0 - transform.position.y; // constrain the box to y = 3
let baumgarte = beta / delta_time * -pos_error;

// Solve the constraint
for _ in 0..iterations {
	let velocity_error = rigid_body.velocity.y;
	let lambda = -(velocity_error + baumgarte) / effective_mass;

	rigid_body.velocity.y += lambda / rigid_body.mass;
}

// Integrate velocity
rigid_body.position.y += rigid_body.velocity.y * delta_time;

Here is a nice frame from Ming-Lun Chou's video linked above where you can reference the equations and compare them to my code.

I'm not able to find a mistake anywhere. Can anyone please help me understand why I'm experiencing these two issues and how I can fix them?

It seems you are missing a dt. You also need to be careful with frequency f and angular frequency omega. Finally make sure you pass in the ‘effective mass’ (the mass seen by the constraint) and not the body mass (as eg the ODE does for ERP/CFM). Here is what I use as a reference:

inline void rnBuildSoftConstraintCoefficients( float& Bias, float& Epsilon, float ConstraintError, float Mass, float Frequency, float DampingRatio, float Timestep )
{
	float Omega = RN_2PI * Frequency;
	float Ks = Mass * Omega * Omega;
	float Kd = 2.0f * Mass * DampingRatio * Omega;

	Epsilon = 1.0f / ( Ks * Timestep + Kd ) / Timestep; // Epsilon = gamma/h
	Bias = Epsilon * Ks * Timestep * ConstraintError;  // Bias = beta/h *  C
}

Also, it seems you are integrating position twice:

// Integrate
rigid_body.velocity.y += acceleration * delta_time;
transform.position.y += rigid_body.velocity.y * delta_time;  // <-- DON'T do this

// Calculate constants
let d = 2.0 * rigid_body.mass * SPRING_ZETA * SPRING_OMEGA;
let k = rigid_body.mass * SPRING_OMEGA * SPRING_OMEGA;

let gamma = 1.0 / (d + delta_time * k);
let effective_mass = (1.0 / rigid_body.mass) + gamma / delta_time;

let beta = (delta_time * k) / (d + delta_time * k);
let pos_error = 3.0 - transform.position.y; // constrain the box to y = 3
let baumgarte = beta / delta_time * -pos_error;

// Solve the constraint
for _ in 0..iterations {
	let velocity_error = rigid_body.velocity.y;
	let lambda = -(velocity_error + baumgarte) / effective_mass;

	rigid_body.velocity.y += lambda / rigid_body.mass;
}

// Integrate velocity
rigid_body.position.y += rigid_body.velocity.y * delta_time;  // <-- ONLY do this

@dirk gregorius Thank you for the reply. I don't believe I am missing a dt, our bias terms are the same (your “Bias” is my “baumgarte”, I've change my variable name to bias in the code below to avoid confusion). Am I missing a dt somewhere else?

I certainly was integration the position twice, thanks for pointing that out. I shouldn't be integrating the position in the first step because it hasn't yet gone through the corrective process of the sequential impulse solver.

One thing I found is that I'm actually missing a term when calculating lambda.​ It should actually be

as derived here.

So I changed my code to incorporate this extra term as well as fix the double integration.

SPRING_ZETA = 0.0;
SPRING_OMEGA = 2.0 * PI;

// Integrate
rigid_body.velocity.y += acceleration * delta_time;
let tentative_position = transform.position.y + rigid_body.velocity.y * delta_time; // Calculate a tentative position which is not applied to the box

// Calculate constants
let d = 2.0 * rigid_body.mass * SPRING_ZETA * SPRING_OMEGA;
let k = rigid_body.mass * SPRING_OMEGA * SPRING_OMEGA;

let gamma = 1.0 / (d + delta_time * k);
let softness = gamma / delta_time;
let effective_mass = (1.0 / rigid_body.mass) + softness;

let beta = (delta_time * k) / (d + delta_time * k);
let pos_error = tentative_position - 3.0; // Use tentative position here
let bias = beta / delta_time * pos_error;

// Solve the constraint
let mut total_lambda = 0.0;

for _ in 0..iterations {
	let lambda = -(rigid_body.velocity.y + bias + softness * total_lambda) / effective_mass; // Here I added softness * total_lambda which I was missing before
	total_lambda += lambda;

	rigid_body.velocity.y += lambda / rigid_body.mass;
}

// Integrate velocity
rigid_body.position.y += rigid_body.velocity.y * delta_time; // Now that the velocity has been corrected, apply it to obtain the final correct position

Now the first issue I mentioned where the oscillation speed would change depending on the number of iterations has been fixed and the position integration is being done correctly.

When zeta is 0, the box still comes to a rest over time. I'm still not sure why this is happening, I expect it to never come to a rest. Am I just misunderstanding how zeta works? This is the result with zeta = 0 and omega = 2pi.

So what is going on here? Am I actually doing things correctly but misunderstanding what happens when zeta is 0? Or am I doing something wrong because when zeta is 0 the box should oscillate forever?

Dirk Gregorius said:
Finally make sure you pass in the ‘effective mass’ (the mass seen by the constraint) and not the body mass (as eg the ODE does for ERP/CFM).

Forgot to touch on this. Are you saying when I calculate the bias term I should be using the effective mass, not the mass of the whole body?

Yes, you must use the effective mass.

See slide 21 and 37+ here: https://box2d.org/files/ErinCatto_SoftConstraints_GDC2011.pdf

I see, so the effective mass is

which, in this situation is just the rigid body mass because 1 / (J * invM * JT) = 1 / (1 / rigid body mass) = rigid body mass. Then we use that to calculate k and c.

Then we can calculate gamma and beta.

Then using the equation

where bias = beta / h * C and softness = gamma, we can find the value for lambda. Taken from the derivation here, we have dP = -(J * v2damaged + softness * P + bias) / (J * invM * JT + softness).

So now the code should be as follows.

SPRING_ZETA = 0.0;
SPRING_OMEGA = 2.0 * PI;

// Integrate
rigid_body.velocity.y += acceleration * delta_time;
let tentative_position = transform.position.y + rigid_body.velocity.y * delta_time;

// Calculate constants
let effective_mass = rigid_body.mass;

let k = effective_mass * SPRING_OMEGA * SPRING_OMEGA;
let c = 2.0 * effective_mass * SPRING_ZETA * SPRING_OMEGA;

let gamma = 1.0 / (c + delta_time * k);
let softness = gamma;

let beta = (delta_time * k) / (c + delta_time * k);
let pos_error = tentative_position - 3.0;
let bias = beta / delta_time * pos_error;

// Solve the constraint
let mut total_lambda = 0.0;

for _ in 0..iterations {
	let lambda = -(rigid_body.velocity.y + bias + softness * total_lambda) / (1.0 / rigid_body.mass + softness);
	total_lambda += lambda;

	rigid_body.velocity.y += lambda / rigid_body.mass;
}

// Integrate
rigid_body.position.y += rigid_body.velocity.y * delta_time;

But this doesn't work either. With softness = gamma, the box snaps to the target position instantly. With softness = gamma / h, the box comes to a rest just like the last .gif I shared.

SPRING_ZETA = 0.0; → This does not make any sense

SPRING_OMEGA = 2.0 * PI; → This is very soft

I would use a damping ratio of 1.0f and a frequency f of 10.0f. This will give you a reasonable stiff critically damped spring. If you want a more bouncy behavior I would use a damping ratio of 0.7 and a frequency f of 5.0f. Don't forget that omega = 2pi * f

Dirk Gregorius said:
SPRING_ZETA = 0.0; → This does not make any sense

Okay so my assumption is wrong that the box would oscillate forever if zeta is 0. I was trying to use that as a way to verify the correctness of the solver. It is behaving correctly though if I compare zeta to 1. When zeta is less than 1, there is oscillation. When zeta is greater than or equal to 1, oscillation is gone and the amplitude decays. And omega seems to affect the amplitude correctly.

Thank you Dirk, I can be confident now that my solver is correct.