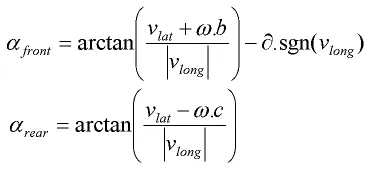
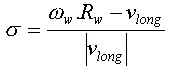Recently i started looking into vehicle physics/simulations and tire friction models.I've looked into the pacejka tire friction model and attempted to apply in a physics engine (bullet physics in this case) in which the chassis is a dynamic rigidbody while the wheels are implemented via a raycast suspension system.My main two references are the car physics article by "Macro Monster"
https://asawicki.info/Mirror/Car%20Physics%20for%20Games/Car%20Physics%20for%20Games.html
and this thesis/master project about car physics for games:
https://nccastaff.bournemouth.ac.uk/jmacey/MastersProject/MSc12/Srisuchat/Thesis.pdf
Here is a simple mockup of how my vehicle setup looks like in the engine: (from the top down perspective):
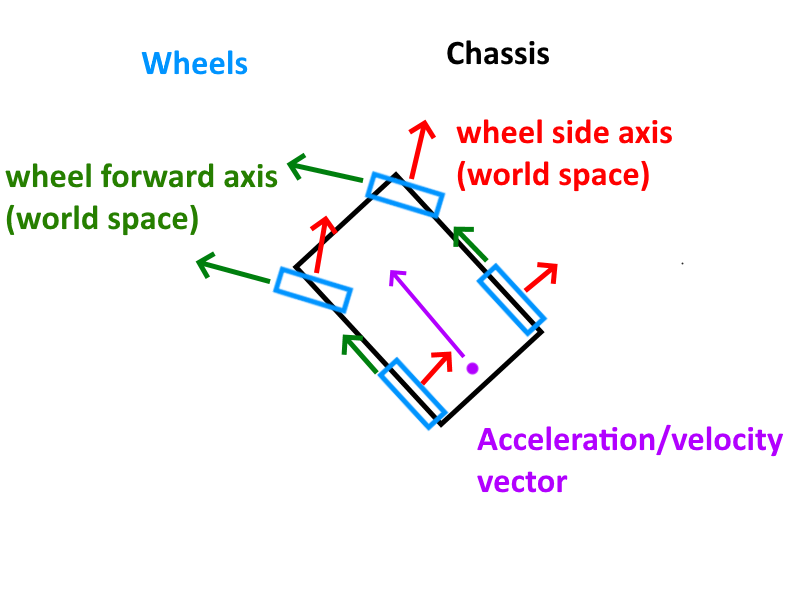
To keep things simple the acceleration/force is applied at the center of the rear axle in the direction of the cars local forward axis. Friction is applied to each wheel seperately. (I know that this setup isn't physically accurate but i wanted to keep things simple for now.) Forces are also applied on the same height level as the center of mass so the car doesn't start to roll in curves. (Weight transfer is in general ignored here. Weight is essentially equally distributed over all wheels/suspensions.) Front wheel ackermann steering is also implemented.
So to implement the lateral friction/cornering force i used the normalized pacejka formula which i took from this wikipedia article: https://en.wikipedia.org/wiki/Hans_B._Pacejka
static float pacejka(float slipAngleDegrees){
float x = slipAngleDegrees;
float B = 0.714;
float C = 1.40;
float D = 1.00;
float E = -0.20;
return D * sin(C * atan(B * x - E * (B * x - atan(B * x))));
}
From my understanding the pacejka formula requires the input parameter (slip angle) to be in degrees and NOT radians. (Although from cross referencing pacejka implementations over the net i've sometimes seen radians used as well. So i'm not entirely sure if that's accurate.)
So now we want to calculate the lateral velocity for each wheel and apply the pacejka formula to it.
In bullet physics rigibodies have a getVelocityInLocalPoint(position) function to return the velocity of a rigidbody in a given point.
Here kind of a pseudocode how the calculation looks like (very simplified): Note that in the example mentioned above i don't apply the force directly at the raycast contactpoint with the ground to avoid body roll. (The pseudocode does that to get the idea along.)
int wheelCount = 4;
for each wheel w{ //we have 4 wheels
vec3 tireVelocity = rigidbody->getVelocityInLocalPoint(w.localContactPoint); //w.localContactPoint is where the suspensionraycast hits the floor relative to the rigidbody origin)
float lateralVelocity = dot(tireVelocity,w.sideAxis); //sideAxis is the red normal in the image shown above which is the wheels side axis in world-space
float longitudinalVelocity = dot(tireVelocity,w.forwardAxis); //green normal in above image
//calculate slip angle
float slipAngleRadians = std::atan2(lateralVel,longitudinalVel);//slipangle in radians
//pacejka requires slipangle to be in degrees.
float slipAngleDegrees = slipAngleRadians * 180.0f/PI;
float pacejkaValue = pacejka(slipAngleDegrees);
float tireLoad = chassisMass * gripValue; //simplification. gripValue = 30.0f; (example)
//calculate lateral force. tireLoad * pacejkaValue / wheelCount
float lateralForce = (tireLoad * pacejkaValue) / float(wheelCount);
//apply lateral force along the wheelsideaxis at its contact point
rigidbody.applyForce(-w.sideAxis * lateralForce,w.localContactPoint);
}
The issue with that implementation is that in curves the car starts oscillating between the current angular velocity and the direction of travel. That's how it looks like in-engine:
Now of course i know that this implementation is a very crude simplification of the tire friction model (as other aspects as weight transfer are ignored) but i'm not sure if the way lateral forces are calculated is correct.
The oscillations you see (the car bobbing left and right after taking a turn until it starts to rest) also happen at lower speeds but it gets more pronounced at higher ones. You can see those oscillations also occur in the graphs on the left side of the screen (lateral pacejka values and lateralforce changes due to the car constantly vibrating left and right) You can even see how the car rapidly spins out at the end which looks completely unnatural. (so maybe my entire approach is wrong.)
My suspicion is/was that the center part of the pacejka formula (where the lateralVelocity gets near zero) the force applied to the wheel also rapidly decreased (marked in red):
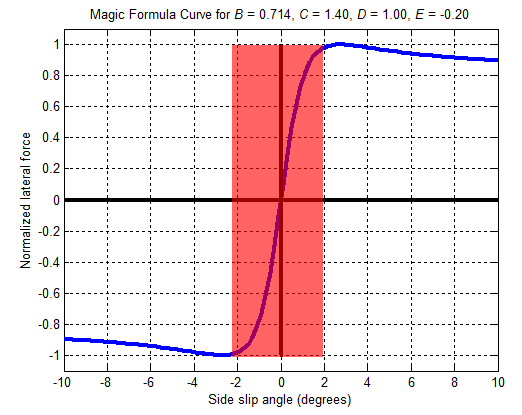
Which in theory might work, the issue however is that (at least from my understanding) the car should essentially have full grip capabilities at those narrow slip angles. But because the lateral forces rapidly decrease at those narrow slip angles the still doesn't have entirely full grip in this range (it rapidly gets there but essentially the car still slides to a small degree) which i think is what causes those oscillations to occur.
My initial thought was that the pacejka formula should look somewhat like this (red line):
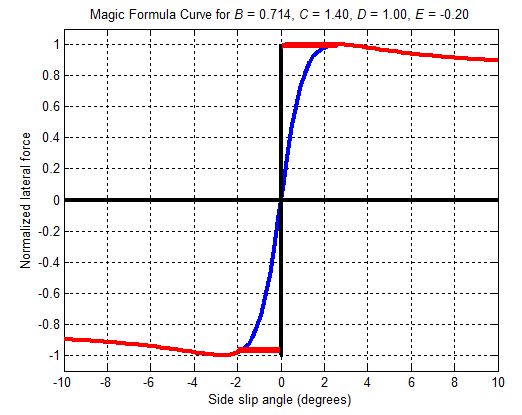
Where the force on the small slip angles is still high enough to “rotate” the car towards its resting position by basically applying enough force to immediately setting its angular velocity the the intended one during a full grip situation (which happens anyway during low speed situations where pacejka cannot be applied.) . But now thinking about it this might not be entirely possible on a fully physics driven system.
Can someone shine more light into this? Is this behaviour shown in the video expected with the current implementation? Or am i overlooking a crucial detail somewhere? (Maybe the slipangle calculation should remain in radians and not degrees?) Woould appreciate any kind of tips/guides into the correct direction.