Hello, I've managed to implement a sequential impulse constraint solver for resolving collisions and now I need to incorporate friction. I've got a question regarding clamping that I can't find an answer to.

Please correct me if I'm wrong but as I understand it, in 3D, you find two orthogonal unit vectors such that their cross product is equal to the collision normal. These two tangent vectors are the directions which you apply the friction impulse in. Then you calculate two corresponding lambdas which are the magnitudes of the two tangent impulses.

That makes sense to me but what I don't understand is the way the two lambdas are bounded. The friction force is proportional to the normal force so we have the following limiter.

In 3D, we have two tangent vectors so we have two lambdas. At 12:00 in Ming-Lun Chou's Contact Constraints video, he limits these two lambdas individually by the normal lambda.

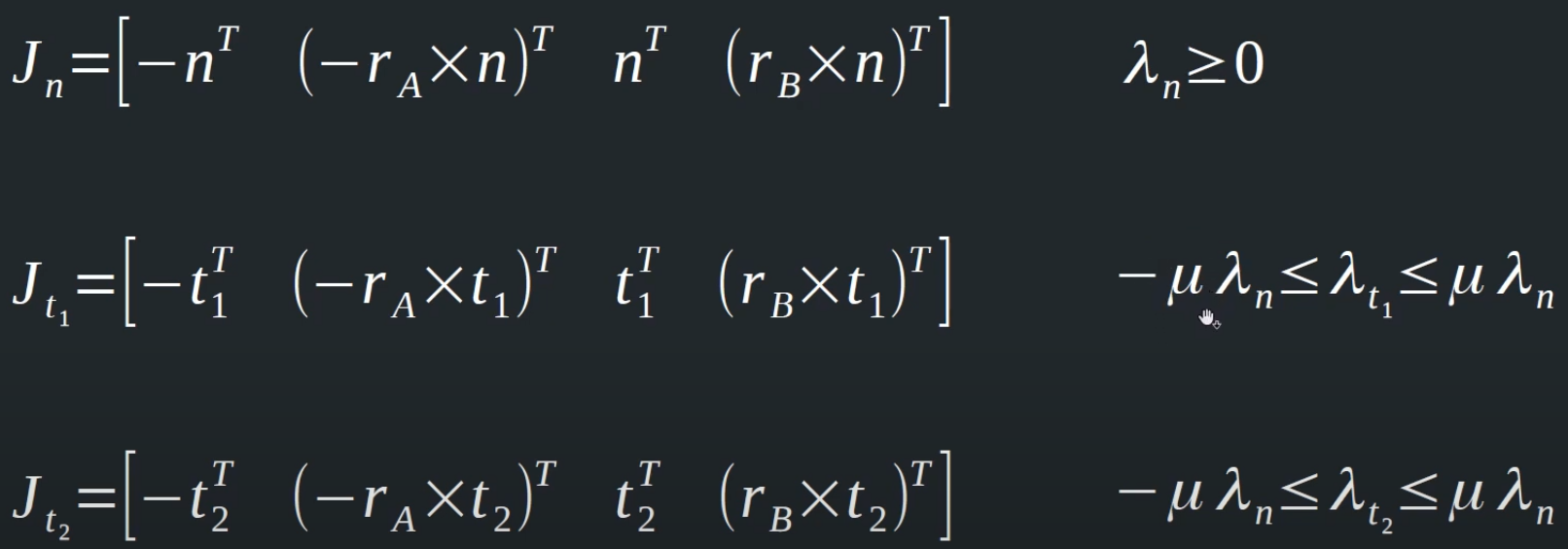
This doesn't seem right to me, we want to limit the total friction impulse by a factor of the normal impulse so I was thinking we should add together the two tangent impulses into one. The length of this combined vector would give us a single lambda which we then apply the limit above to. If you limit the two lambdas individually, the combined fiction force could still be past the limit right? Imagine two orthogonal vectors with a length of 1, once combined the total length is sqrt(2). If your limit is 1, then the individual vectors are correctly limited but the sum of the two is not so we must limit the single combined lambda.

On page 12 of Eric Catto's Iterative Dynamics with Temporal Coherence paper, he gives a different approach where he limits the two lambdas separately without any mention of the normal lambda.

I don't understand, why is there an awkward coupling and how are things made more complicated? He also says this approach leads to unrealistic behavior since the normal force does not affect the strength of the friction. So why can't we use the previous mentioned technique which does use the normal force?

I'm just confused, the answer seems simple. First find the normal lambda and normal impulse. Apply the normal impulse. Then find the total friction impulse, calculate it's magnitude which yields a single lambda, then limit that like so.

Does that make sense? If not, could you help me understand the correct way to handle friction?

Erin's approach is very old and this was suggested to avoid the coupling between the friction and non-penetration impulses. This way it actually stays an LCP since the limits are constant. The first approach you suggest is actually totally fine and should work fine in practice. Note that the system is now technically not an LCP anymore since the friction limits depend on the non-penetration impulses. But don't worry about this. This works just fine in practice. Also technically you are clamping against a box and not a cone. But I would not worry about this right now as well.

I've implemented the first approach of clamping the friction impulse to +/- the accumulated normal impulse and experienced no problems. You can clamp the friction either separately along each tangent direction (producing a friction “pyramid”), or it's also possible to clamp both tangent directions together using a projection of the (tangentX,tangentY) vector onto an ellipse (producing a friction “cone", which is more realistic). Basically, compute the magnitude of the 2D tangent impulse vector, then scale it down if it is outside the circle with radius = mu*I_z (an ellipse with anisotropic friction). All clamping should be done on the total accumulated impulse for the time step, not the impulse for a solver iteration.

@Dirk Gregorius @Aressera Thank you for the help that all makes sense. I was also reading Allen Chou's Contact Constraints article and he touches on this topic.

He says “You might notice that this clamping method is not perfect. We can end up with clamping the magnitude of total tangential impulse to sqrt(2) * C_F * lambda_n. However, this error is usually not noticeable, so I usually just let it be (Joshua Davis, a member of DigiPen Institute of Technology, informed me of this idea).”

So even though clamping along the individual tangents might not be as accurate as clamping the total, that error isn't noticeable so it may not be worth complicating things further.

Thanks again for the help, my physics solver is behaving pretty realistically now!