Hello, I've managed to implement a sequential impulse constraint solver for resolving collisions and now I need to incorporate friction. I've got a question regarding clamping that I can't find an answer to.
Please correct me if I'm wrong but as I understand it, in 3D, you find two orthogonal unit vectors such that their cross product is equal to the collision normal. These two tangent vectors are the directions which you apply the friction impulse in. Then you calculate two corresponding lambdas which are the magnitudes of the two tangent impulses.
That makes sense to me but what I don't understand is the way the two lambdas are bounded. The friction force is proportional to the normal force so we have the following limiter.
.png)
.png)
In 3D, we have two tangent vectors so we have two lambdas. At 12:00 in Ming-Lun Chou's Contact Constraints video, he limits these two lambdas individually by the normal lambda.
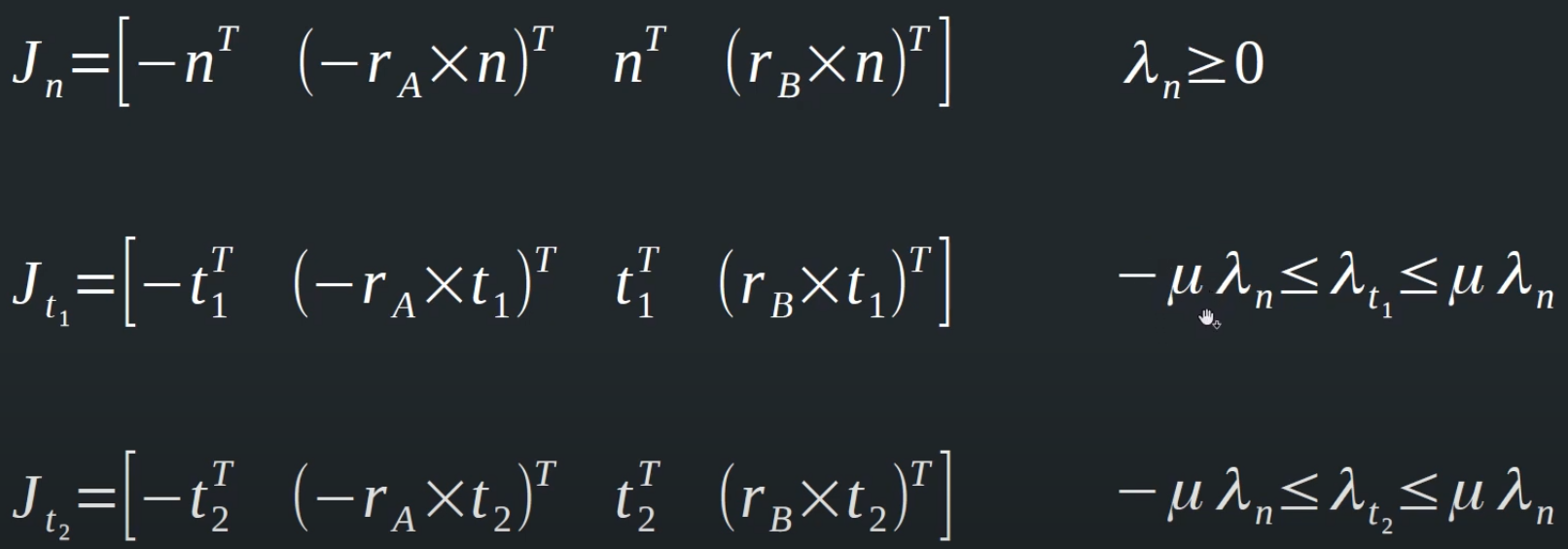
This doesn't seem right to me, we want to limit the total friction impulse by a factor of the normal impulse so I was thinking we should add together the two tangent impulses into one. The length of this combined vector would give us a single lambda which we then apply the limit above to. If you limit the two lambdas individually, the combined fiction force could still be past the limit right? Imagine two orthogonal vectors with a length of 1, once combined the total length is sqrt(2). If your limit is 1, then the individual vectors are correctly limited but the sum of the two is not so we must limit the single combined lambda.
On page 12 of Eric Catto's Iterative Dynamics with Temporal Coherence paper, he gives a different approach where he limits the two lambdas separately without any mention of the normal lambda.

I don't understand, why is there an awkward coupling and how are things made more complicated? He also says this approach leads to unrealistic behavior since the normal force does not affect the strength of the friction. So why can't we use the previous mentioned technique which does use the normal force?
I'm just confused, the answer seems simple. First find the normal lambda and normal impulse. Apply the normal impulse. Then find the total friction impulse, calculate it's magnitude which yields a single lambda, then limit that like so.
.png)
Does that make sense? If not, could you help me understand the correct way to handle friction?







