Let's say I have a staff weapon that has two grab points:

The player is able to grab both points at the same time, and if he does grab both points, I want to rotate the staff relative to the angle of both points.

Another example would be a two handed firearm like an assault rifle. In VR you're able to angle the weapon using your second arm.

I'm using Unity and already figured out how to grab two points at the same time in VR. I just have no idea how to accomplish the rotation, aka Maths :(

Any suggestions are welcome, thanks!

It's surely easy to solve, but first notice your problem is not yet well defined.

If you have two points, there's a line between them, and the stick should align to that.
But if we hold the stick at two ends, we can still rotate the stick around this this line, so you need one more constraint to define this, usually people use an up vector.

Though, i assume this is like a Billiard game? And it does not matter how the stick is oriented other than being aligned?
If so, we would instead say ‘the stick should not rotate around the line, and it's angle around that line never matters’.

The code could look like this:

matrix3x3 AlignedOrientation (vec3 point1, vec3 point2, matrix3x3 currentOrientation)
{
// assuming the stick model is alignid along it's local X axis

	vec3 currentDir = normalize(currentOrientation[0]); 
	vec3 targetDir = normalize(point2 - point1);
	vec3 axisOfRotation = normalize(cross(currentDir, targetDir));
	float angleOfRotation = acos(currentDir.Dot(axisOfRotation));
	
	matrix3x3 rotation = matrix3x3::FromAxisAndAngle(axisOfRotation, angleOfRotation); // Unity surely has this somehere, if not look for it at Quaternions.
	return currentOrientation * rotation; // or vice versa - not sure about Unitys multiplication order convention
}

Thank you! Very straight forward explanation, this is going do the trick!

Anytime you use trigonometry to solve a 3D problem, you're probably doing it wrong.

The ONLY time trigonometry is the right solution, is when you start with a measurement in degrees. This is the case when you have user input from a mouse, or when you have animation keyframes that use degrees (or radians.)

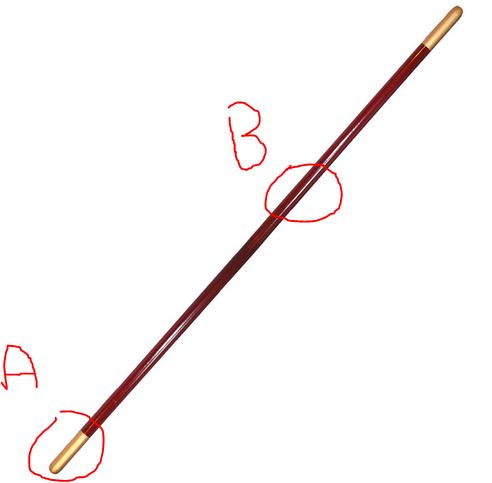
In the current case, there's a much easier way to recover the orientation matrix: Simply use the points as your basis vectors.

Let's say that the staff is modeled such that the “base to tip” direction is the X axis in the original model space.

Then, the X vector of your world orientation matrix is simply Xout = normalize(B - A)

The next step is to get the “up” vector. Assume this is “Y” in the model's original space. Use the world's up vector for the desired target, unless you have a full orientation value for the points A. (If you have the full orientation of point A, use its up vector)

So, the “up” vector (Y in this case) is the world-up, made orthogonal to your “forward” vector. Let's say your world uses “Z up." Thus, the Y vector of your orientation matrix is Yout = fabsf(dot(Xout, Z)) > 0.999f ? Forward : normalize(Z - dot(Xout, Z) * Xout)

What's with the conditional? Well, when the user points the staff straight down, or straight up, there's no well-defined separate “up” because the staff-forward is also world-up. We pick an arbitrary axis at this point; I'm choosing Forward (which should be the user's forward vector) but you can pick whatever. It will approximately neve rhappen, but when it does, you don't want divisions by zero and NaNs in your matrices.

OK, we have “forward” and “up,” and they are orthonormal, so all we need to do is recover “right” using cross product:

Zout = cross(Xout, Yout)

Your rotation matrix then uses these vectors as its basis vector:

OutRotation = Matrix3(Xout, Yout, Zout)

Note that this is quite similar to the “lookat” matrix, except it's forward instead of inverse. Thus, you could just use whatever lookat function you have, to look at B from A, and then transpose the matrix.

hplus0603 said:
The next step is to get the “up” vector. Assume this is “Y” in the model's original space.

Just to clarify the difference between your proposed up vector method and mine…

• The up vector method causes flipping if the global and local up vectors become 90 degrees apart.
  It is thus only applicable if we can surely prevent such cases, but preferred if we want to keep things upright.
• The axis and angle method flips if the target line is 90 degrees apart from the current stick.
  It depends only on the stick and the target, so often behaves more natural / predictable, and robust. But if the objects visuals imply some sense of ‘upwards’, we may feel the desire to ‘fix’ their current twisted appearance, without a way to do so.

So, i'd say - for a VR Billiard game use axis-angle, to hold a box in Portal use up-vector.
Though, tbh i think neither of those simple methods is good enough for the difficult problem of modeling physically plausible but responsive interaction with a virtual worlds objects, but it's a start.

hplus0603 said:
Anytime you use trigonometry to solve a 3D problem, you're probably doing it wrong.

I like that ‘probably’ in this assumption. : )

hplus0603 said:

Thanks for this detailed reply!