I have read the original Position Based Dynamics paper (https://www.cs.toronto.edu/~jacobson/seminar/mueller-et-al-2007.pdf).​ There is the pseudo-code on the 3rd page. I implemented it exactly.

Let's run this for a case of a single particle (i.e. no constraints), which only gravity acts on. See the picture below:

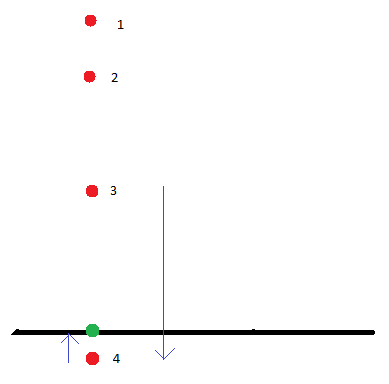
We start with position red1. After the first step it goes to red2, then red3. In the next step we have red3 position and velocity represented by the blue arrow to the right. We end up in position red4, penetrating the ground. Now we have to react. We push the position out to position green. We then calculate the velocity (step 13. in the pseudo-code). The result is the velocity vector to the left. As you can see, by only working with positions we end up with a particle that after the collision is left with way less energy than before the collision. But that is not the worst part. The worst part is that this resulting post-collision velocity will be different depending on how deeply red4 position is penetrating. If it happens to be penetrating shallowly (as in the case above) the post-collision velocity is small. If the penetration is deep then the post-collision velocity can be even almost as big as the pre-collision velocity.

Is this how it's supposed to work? What would be the elegant way to make the particle bounce without losing any energy, for instance?

AFAICT pure PBD isn't concerned with maintaining energy, it's concerned with stability (so, losing excess energy from the system might even be a benefit). This is why it's typically used for cloth or other systems where you don't want bouncing.

In your example, the particle will still have quite a bit of downwards velocity after step 4 (add step 3 and step 4 velocity vectors and you get a large downward vector), you'll need to step once more to get rid of the velocity error (ie step 5 will be positioned coincidently with step 4, zero-ing the velocity).

Bouncing specifically (similar to friction) is difficult to capture with PBD because it depends on velocities, not positions. More recent PBD papers have presented position-based formulations of friction, but I don't know of any that deal with bouncing – IME bouncing is not something you really want from a physics engine, it's better left for game logic. AFAIK no physics engine really does bouncing correctly, at least IIRC last time I looked at Box2D it was really only designed for inelastic collisions.

In the past what I've done is, after the physics step (so: positions+velocities are updated), if there was a collision, check if the velocity points against the surface normal, and if so manually reflect the velocity across the tangent plane.

You could also consider solving at both the position and velocity level (see eg Box2D which I think has an example of this). This is pretty analogous, however it means you need to calculate a whole new set of gradients/jacobians, which can be tedious and error-prone. The idea is to step the sim something like this:

-integrate positions forward

-solve position constraints via PBD

-integrate velocities forward

-solve velocity constraints via PGS (ie clamped impulses as in Box2D)

However, I've always had stability problems with the above, probably because it's akin to explicit Euler (we're stepping the positions before the velocities). However AFAICT many PBD solvers use something like this (see the work of Jan Bender https://github.com/InteractiveComputerGraphics/PositionBasedDynamics​ )