I`m looking to perfect my pathfinding algorithm. When you use A* the main reason you check the neighbour tiles is because you want to see if you can advance the current track/there are no obstacles in the way. But when do you decide that you want to open a new track/branch?

Calin said:
But when do you decide that you want to open a new track/branch?

At every iteration, you add one path segment.

An efficient implementation adds always the shortest segment to the set of visited nodes first (using something like a priority queue).

A simple implementation (like mine from last thread) adds any segment to the set, but ensures the segment is the shortest to the selected node.

Here a nice A* animation from wikipedia:

Notice the difference between Dijkstra and A* is:

Dijkstra only measures the path length to the start to vote for the best next segment.

A* also uses the distance to the goal to measure which segment is the best next choice.

My simple example is like Dijkstra, it just processes nodes in the order of BFS (Breadth First Search). It gives the same result as optimized Dijkstra but takes more steps to get there. (Similar to how Dijkstra needs more steps than A* but result is the same.)

So, to learn this, do it in this order: BFS (fundamental building block to traverse trees and graphs), Dijkstra, A*

My simple example is not my invention, it is just BFS with additional tracking of the previous node so we can build a path after the goal has been reached. It's the simple way of path finding, and every programmer gets to this same solution. You should too, and i can only advise again to understand just this at first.

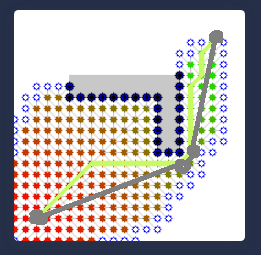
Now take a look at the picture and see how it is a process of region growing or flood fill, which is what BFS is doing. It starts at a node, adds all unvisited but reachable neighbous to a stack, than loops to the next node on the stack and adds its neighbors too, until all nodes have been processed or the goal has been found. (A picture of Dijkstra would be a better illustration - the visited set would grow like a circle)
A key property here to grasp is that the Dijkstra algorithm does not care about the goal or paths at all. It just grows until done, and only after that we construct the path by tracking from the goal to the start following the nodes that added the current as their next neighbor to visit.

After that's clear, the main problem to master becomes only to understand BFS, so using the stack to have that region growing working.

If you do breadth-first traversal with the tiles closest to the goal first, you can just keep consuming tiles from the active list while adding new neighbors to check later. Then you can stop adding neighbors to the active list once all origins have an eight-way optimal path to the goal. This prevent traversing huge worlds when just moving to a place nearby.

Dawoodoz said:

If you do breadth-first traversal with the tiles closest to the goal first, you can just keep consuming tiles from the active list while adding new neighbors to check later. Then you can stop adding neighbors to the active list once all origins have an eight-way optimal path to the goal. This prevent traversing huge worlds when just moving to a place nearby.

I think what's meant by this is: If you have one goal but many origins (i called it ‘starts'), then it's better to start form the goal, and stop after all origins have been found.
That's a nice example of how the region growing makes sense, and also a nice example of Dijkstra being better than Astar becasue Astar supports only one goal for its scoring heuristic, i guess?).

Another optimization is, if we only have one goal and start, we can grow from both points instead only one and stop after both regions meet each other. This processes only ⅓th of nodes usually.

But we discussed those already and it's advanced stuff that's good to know but… not yet :D

So you don`t open new paths along the way, you generate paths in all directions from the beginning and see which one turns out to be good.

Calin said:

So you don`t open new paths along the way, you generate paths in all directions from the beginning and see which one turns out to be good.

Use breadth-first traversal with same cost steps or sort them, which is the simplest fast way. To prove that there cannot be any shorter path, all lose ends must have reached the same total distance.

Proof of correctness: If B ≥ A and N ≥ 0, then B + N ≥ A. A is the successful paths. B are undiscovered paths along the seam of not iterated tiles. N is the added cost of taking additional steps in the unknown, assuming that no unit travels back in time.

So you don`t open new paths along the way, you generate paths in all directions from the beginning and see which one turns out to be good.

Exactly. It appears dumb and brute force, but those algorithms can solve hard problems like labyrinth where any line of sight approach would fail.

In a game i would first trace a ray to the goal and only if there are obstacles use path finding.

You can combine both to make some complicated but more efficient algorithm, but the most potential for optimization would be to simplify the graph of the map.

For example:

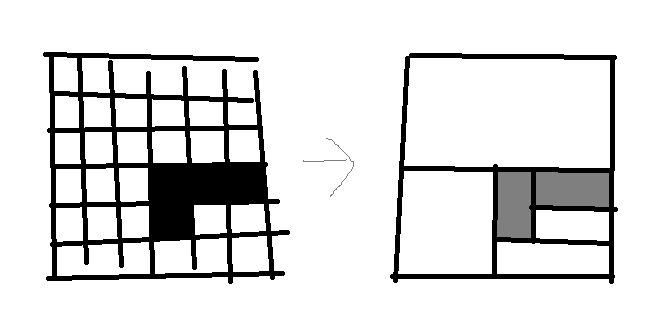
From 36 nodes to 6 nodes. Path finding will be fast. (Methods of simplification would be BSP tree or motorcycle graph. The latter can be realtime more easily - if necessary.)

The path finding algorithm now needs to support nodes with variable number of adjacent neighbors. That's the general form of path finding anyways - the grid is just a typical special case often used in games.

After the path have been found, it can be improved with line of sight tests. So going from the start check the path until an node is no longer visible and add a vertex there and continue:

With grids that's optional maybe, but with simplified graph it becomes necessary i guess. After that it's common turn those line segments into curves to make motion more naturally.

This simplified graph approach is what's called ‘Navmesh’ in games.

Further optimizations would be:

Adding hierarchy of way points on top, e.g. with precomputed paths between them.

Make path finding a system that cam process N steps per frame, so computing a long path can not hurt frame rate. Results may need several frames to become available, but that's usually no problem.

My previous pathfinding would generate children path segments from from All neighbour tiles found in the pool when an obstacle was hit, and advance from that tile from the pool which has the lowest cost. Saving everything to a common pool means there aren`t distinct paths. It`s just a huge cancer that grows from the cheapest tile.

Calin said:
My previous pathfinding would generate children path segments from from All neighbour tiles found in the pool when an obstacle was hit, and advance from that tile from the pool which has the lowest cost. Saving everything to a common pool means there aren`t distinct paths. It`s just a huge cancer that grows from the cheapest tile.

There are many algorithms that use similar strategy than what you describe. They can be ofc. faster, and they succeed most of the time but they can get stuck. (I saw a nice page with javascript testcases for many such algorithms, but can't find anymore.)

So you need the cancer growing in any case for fallback in case of failure, but:

Detecting failure early might be costly.

On failure, you can get worse performance because the runtime of both algorithms add. But in games we have to optimize for the worst case. An algorithm that is faster on average but causes spikes in runtime is bad, even if it happens only rarely.

So… it is hard, but best to accept the cancer growing is necessary. It becomes easier to accept after realizing it is indeed the best option (and A* really fixes problem if applicable).
At this point, dreams of intelligent Terminators drain down the closet, because we realize computers are totally dumb. :P

For consolidation: Even my simple example is much faster than your algorithm in general. I can be sure of that even without understanding your algo in detail just by looking at the nested loops you have.

My proposal would be this now:

1. Start from scratch.
2. Implement BFS only for growing the cancer, ignoring paths and pointers to previous nodes. This is not that slow because it visits each node only once. Visualize how stuff grows and enjoy seeing it working.
3. Add the links to previous nodes which requires updating information so we have the shortest path to the start from everywhere, not just any path which might be bad and unpredictable for the player.
4. Add early termination after the goal(s) has been found and extract the path.
5. Be happy and move on until performance problems show up. (likely they won't)
6. Eventually implementing priority / fibonacci queue would be the next step. But that's harder than all the above together already. (Or just use std::priority_queue)
   Eventually use hash map to avoid storing all stuff in a huge world maps memory. This is only a win if world is huge but paths are short in relation.

I think that's a good strategy so you progress in smaller steps, and you learn patterns of algorithms that are reusable for other things later. The result should be simpler and faster than what you have now.

EDIT: Because i never implemented Astar i can not advise if doing this, or first just Dijkstra would be a good idea. I only know the difference between the two is only cost calculation which is one line of code.

Thanks for perspective JoeJ, using a better algorithm will work best with the game I want to make so I`m just exploring catching better options. Btw JoeJ I`m using the stuff you`re showing me to other algorithms as well.

Dawoodoz thanks