I'm trying to perform continuous collision detection between a particle (with linear and angular displacement) and a convex hull.

I've read Real-Time Collision Detection by Christer Ericson and in chapter 5 section 3.8 he describes how to determine the time of impact between a line segment and a convex hull (which is represented by the intersection of a set of planes).

The idea is to clip the line segment by each plane and if a segment with a non-zero length remains, then pick the smallest time 't' and that's your time of impact.  I've drawn an illustration:

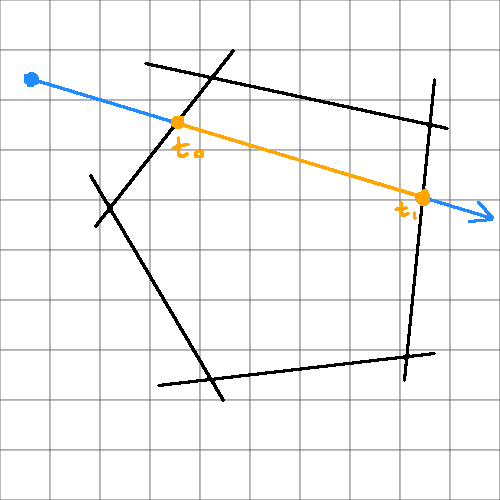
My problem is this works for linear displacement, but the book does not discuss how to account for angular displacement.

Setting aside the convex hull for a moment I think my problem can be simplified as having to find the time of impact between a point (with linear and angular displacement) and a plane.  If I can compute this, then to make it work for a convex hull, I believe I can clip its path and pick the smallest 't' as Ericson described for linear displacement.

I think angular displacement by itself (without linear displacement) can be computed by finding the angle between the particles position vector and a vector perpendicular to the plane.  I've illustrated this idea below in 2D:

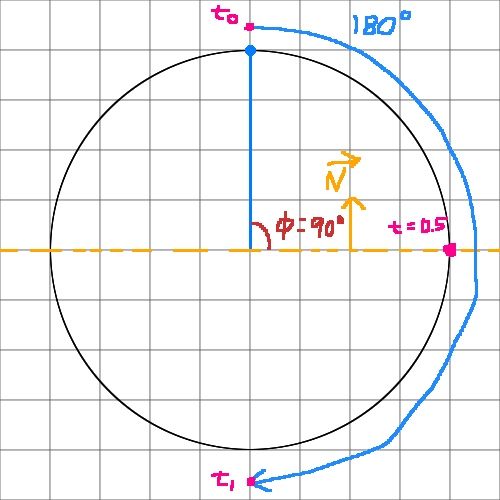
The blue particle starts at t0 = 90° and ends at t1 = -90° (that's an angular displacement θ = -180°).  My "plane" is represented by an orange dashed line.  If we find the angle Φ between the plane's perpendicular vector and the original start position, we get Φ = 90°.  So the time of impact is Φ/θ or 90°/180° = 0.5.

I'm not sure if my solution is entirely correct and even if this does work, how do I account for both linear and angular displacement together?

The following illustration shows a particle with a linear Y displacement of ~1.9 unites and an angular displacement θ = -180°.

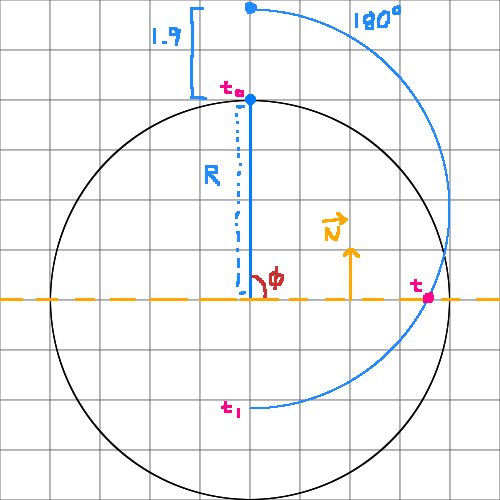
I can't use the method described above because the time of impact extends beyond the angle Φ. This is because the particle is rising and rotating simultaneously making the angle at the time of impact closer to 120°.

Does anyone have any ideas on this?

Anyway if you dont know the particle velocity and angular velicity you can speculate else you iterate the simulation until you find the collision then you return the time (that means each iteration you have a particle pos destination pos for another iteration and a static rotation between frames so you ahould be able to rotate whatever planes or vertices you use

AFAIK the trajectories won't be circular arcs. I think the appropriate search term is “conservative advancement” for iteratively finding the time of intersection. Erin Catto gave a talk on a method he calls “bilateral advancement” which solves this problem, might be worth checking out: https://twvideo01.ubm-us.net/o1/vault/gdc2013/slides/824737Catto_Erin_PhysicsForGame.pdf